7. Системы эконометрических уравнений.

Объектом статистического изучения в экономике являются сложные системы. При использовании отдельных уравнений регрессии изменение факторов влечет за собой, как правило, изменения во всей системе взаимосвязанных признаков. Именно поэтому в последние десятилетия в экономических, биометрических и социологических исследованиях важное место заняла проблема описания структуры связей между переменными системой одновременных уравнений, называемых также структурными уравнениями. В них одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы

y₁=b₁₂y₂ + b₁₃y₃ +…+ b_1ny_n+ a₁₁x₁+ a₁₂x₂+…+ a_1mx_m+ε₁,

y₂=b₂₁y₁ + b₂₃y₃ +…+ b_2ny_n+ a₂₁x₁+ a₂₂x₂+…+ a_2mx_m+ε₂,

…………………………………………………………………..

y_n=b_n1y₁ + b_n2y₂ +…+ b_nn-1y_n-1+ a_n1x₁+ a_n2x₂+…+ a_nmx_m+ε_n.

Зависимые переменные (у), число которых равно числу уравнений в системе, называются эндогенными переменными, предопределенные переменные (х), влияющие на эндогенные переменные, но не зависящие от них, называются экзогенными переменными.

Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно получать целевые значения эндогенных переменных.

Примером системы одновременных уравнений может служить модель динамики цены и заработной платы вида

y₁=b₁₂y₂ + a₁₁x₁ + ε₁,

y₂=b₂₁y₁ + a₂₂x₂+ a₂₃x₃+ε₂,

где y₁ – темп изменения месячной заработной платы;

y₂ – темп изменения цен;

х₁ – процент безработных;

х₂ – темп изменения постоянного капитала;

х₃ – темп изменения цен на импорт сырья.

В отличие от предыдущих разделов каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются следующие специальные приемы оценивания:

– косвенный метод наименьших квадратов;

– двухшаговый метод наименьших квадратов;

• трехшаговый метод наименьших квадратов;

• метод максимального правдоподобия с полной информацией;

• метод максимального правдоподобия при ограниченной информации.

Данные методы подробно описаны в литературе [6], первые два являются традиционными, достаточно легко реализуемыми.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации, разработанный в 1949 г. Т.Андерсоном и Н.Рубиным. В этом методе сняты ограничения на параметры, связанные с функционированием системы в целом. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего.

Дальнейшим развитием ДМНК является трехшаговый метод наименьших квадратов, предложенный в 1962 г. А.Зельнером и Г.Тейлом. Однако при некоторых ограничениях на параметры более эффективным оказывается все же ДМНК. Метод получил название двухшагового метода наименьших квадратов, ибо дважды используется МНК: на первом шаге при определении формы модели зависимости эндогенных переменных только от экзогенных (так называемая приведенная модель) и нахождении на ее основе оценок теоретических значений эндогенных переменных, и, затем, на втором шаге, используя эти теоретические значения эндогенных переменных, применительно к исходным уравнениям модели. См. также [4].

Практикум

Задача 1. Оценить регрессию, построить график, найти коэффициент корреляции, стандартные ошибки коэффициентов регрессии, дать интерпретацию уравнению регрессии и коэффициентов корреляции.

А)

x	1351.7	1369.3	1479.1	1682.5	1799.0	1924.5	2046.0
y	117,9	122,5	125,5	129,2	134,3	138,4	141,0

Здесь х – совокупные личные доходы;

y – текущие расходы на одежду, среднестатистической американской семьи с 1976 по 1982 г.

Оценим регрессию

y=78,967+0.031x

Найдем коэффициент корреляции:

r_xy=0.986

Построим график:

Вывод: С каждого дополнительного доллара американская семья в период 1976-1982 г. тратила 3,1 центов на текущие расходы на одежду.

Б)

x	1351.7	1369.3	1479.1	1682.5	1799.0	1924.5	2046.0
y	164,3	173,7	181,3	243,2	337,9	376,4	356,6

Здесь х – совокупные личные доходы;

y – текущие расходы на бензин, среднестатистической американской семьи с 1976 по 1982 г.

Оценим регрессию

y=-281,825+0.327x

Найдем коэффициент корреляции:

r_xy=0.962

Построим график:

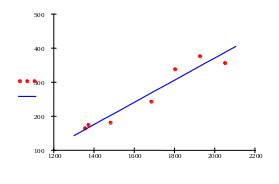
Вывод: С каждого дополнительного доллара американская семья в период 1976-1982 г. тратила 32,7 центов на текущие расходы на бензин.

Задача 2. Вычислить коэффициенты регрессии общей суммы налогового сбора (переменная y) на сумму поступлений налога на добавленную стоимость (х) данным:

Время наблюдения	y, млрд. руб.	x, млрд. руб.	xi2	yi2	xiyi
январь	38,9	13,4	179,56	1513,21	521,26
февраль	45,3	15,4	237,16	2052,09	697,62
март	61,1	16,7	278,89	3733,21	1020,37
апрель	70,4	16,2	262,44	4956,16	1140,48
май	63,8	13,0	169	4070,44	829,4
июнь	67,7	15,0	225	4583,29	1015,5
июль	70,6	20,8	432,64	4984,36	1468,48
август	78,9	16,4	268,96	6225,21	1293,96
сентябрь	73,2	17,4	302,76	5358,24	1273,68
октябрь	78,1	23,6	556,96	6099,61	1843,16
ноябрь	103,0	23,9	571,21	10609	2461,7
декабрь	133,4	34,4	1183,36	17795,56	4588,96
Σ	884,4	226,1	4667,94	71980,4	18154,6
среднее

Г рафик уравнения регрессии y на x выглядит следующим образом:

Задача 3. у= b +ах b и а - ?

а = nxy-x*y

nx²-(x)^{2    }

b = y-bx

n ^

№	Х	Y	X2	XY
1	-3	-0,71	9	2,13
2	-2	-0,1	4	0,02
3	-1	0,51	1	-0,51
4	0	0,82	0	0
5	1	0,88	1	0,88
6	2	0,81	4	1,62
7	3	0,49	9	1,47
Сум 	0	2,79	28	5,61

а = 7*5,61-0*2,79 = 39,27 = 0,20 y= b +аx

7*28-0² 196 y= 0,40+0,20x

b = 2,79-(0,20)*0 = 0,40 -уравнение линейной регрессии

Задача 4. х - мощность пласта, у - смена добычи угля.

№	Х	Y	X2	XY
1	8	5	64	40
2	11	10	121	110
3	12	10	144	120
4	9	7	81	63
5	8	5	64	40
6	8	6	64	48
7	9	6	81	54
8	9	5	81	45
9	8	6	64	48
10	12	8	144	96
Сум 	94	68	908	664

a = 10*664-94*68 = 1.02

10*908-(94)²

b = 68-(-2,75)*94 = -2.75

10

Уравнение регрессии

y= 1,02x-2,75.

Коэфф. корреляции

R = n*xy-xy = 10*664 - 94*68 =0.866

(n*x²-(x)²)(n*y²-(y)²) (10*908-(94)²)(10*496-(68)²)

Связь между Х и Y ближе к линейной.

Коэфф. детерминации R² R1

 0.866² = 0.749  на 74,9% смена добычи угля зависит от мощности пласта и 25,1% от других факторов.

Задача 5. В таблице указаны парные коэффициенты корреляции. Проведите анализ целесообразности включения заданных факторов в уравнение множественной линейной регрессии.

	y	x1	x2	x3	x4
y	1
x1	0,71	1
x2	0,58	0,53	1
x3	0,08	0,2	0,13	1
x4	0,62	0,81	0,3	0,25	1

РЕШЕНИЕ. Между y и x₃ связь практически отсутствует. Между y и x₁ связь сильная, между y и x₂, x₄ – умеренная.

Отсюда следует вывод о нецелесообразности включения фактора x₃ в уравнение множественной линейной регрессии (коэффициент парной корреляции с у равен 0,08).

Между факторами x₁ и x₄ существует сильная прямая связь (коэффициент парной корреляции > 0,8). Для того, чтобы избежать явления мультиколлинеарности, один из этих факторов должен быть исключен из анализа. Исключается фактор x₁, умеренно коррелирующий с x₂ (коэффициент их парной корреляции равен 0,53).

Факторы, включенные в модель множественной регрессии: x₂, x₄.

Задача 6. По некоторым территориям районов края известны значения средней суточного душевого дохода в у.е. (фактор X) и процент от общего дохода, расходуемого на покупку продовольственных товаров (фактор Y).

Требуется для характеристики зависимости У от X рассчитать параметры линейной, степенной, показательной функции и выбрать оптимальную модель (провести оценку моделей через среднюю ошибку аппроксимации (А) и F-критерий Фишера.

Район	у	х
Пожарский (1)	68,8	45,1	61,277	7,5231	11,4989	56,5970
Кавалеровский (2)	61,2	59,0	56,4689	4,7311	2,00817	22,3833
Дальнегорский (3)	59,9	57,2	57,0915	2,8085	0,63123	7,88767
Хасанский (4)	56,7	61,8	55,5004	1,1996	5,69109	1,43904
Лесозаводский (5)	55,0	58,8	56,5381	1,5381	1,81683	2,36575
Хорольский (6)	54,3	47,2	60,5505	6,2505	7,09956	39,0687
Анучинский (7)	49,3	55,2	57,7833	8,4833	0,01055	71,9664
итого	405,2			32,534	28,7563	201,708
среднее	57,886			4,6477

РЕШЕНИЕ.

1а. Для расчета параметров а и b линейной регрессии у=аx+ b решаем систему нормальных уравнений относительно а и b (или используем EXCEL).

Получаем уравнение регрессии: у = 76,88 – 0,35x.

С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта.

Рассчитаем линейный коэффициент парной корреляции: r= -0,35326.

Связь умеренная, обратная.

Определим коэффициент детерминации:

R² = 0,1248.

Вариация результата на 12,5% объясняется вариацией фактора х. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения (см.табл.).

Найдем величину средней ошибки аппроксимации А:

(4,647744/57,88571)100%=0,080292.

В среднем расчетные значения отклоняются от фактических на 8,03%.

Рассчитаем F-критерий:

Fтабл = 6,6 > Fфакт, при γ = 0,05.

Полученное значение указывает на необходимость принять гипотезу Н₀ о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.

1б. Построению степенной модели у= bx^а предшествует процедура линеаризации переменных. Линеаризация производится путем логарифмирования обеих частей уравнения:

lgy = lg b + a lgх , или Y = С + аХ,

где Y = lg(y), X = lg(x), C = lg(b).

Для расчетов используем формулы для линейной регрессии(или используем EXCEL).

Получим уравнение: у = 190,03х^-0,2984 . R² =0,1157.

Характеристики степенной модели указывают, что она несколько хуже линейной функции описывает взаимосвязь.

1в. Построению уравнения показательной кривой у=bа^х предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:

lgy = lg b + хlgа , или Y = С + хlgа, и опять же можно использовать формулы для линейной регрессии(или EXCEL).

Получим уравнение: у = 77,24е^-0,0053х . R² =0,1026.

Показательная функция еще хуже, чем степенная, описывает изучаемую зависимость.

1г. Уравнение равносторонней гиперболы у=а/x+ b линеаризуется при замене: x = 1/z .

Тогда у=аz+b. Для расчетов используем формулы для линейной регрессии(или используем EXCEL).

Получено уравнение: у = 38,435 + 1054.7/x. R² =0.1539.

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи (по сравнению с линейной, степенной и показательной регрессиями). A остается на допустимом уровне: 8,1%.

Следовательно, принимается гипотеза Н₀ о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.

Задача 7. Построить модель связи между указанными факторами, проверить её адекватность, осуществить точечный и интервальный прогноз методом экстраполяции.

7.1. Исходные данные отложить на координатной плоскости и сделать предварительное заключение о наличии связи.

Таблица 1 Диаграмма 1

x	y
2,1	29,5
2,9	34,2
3,3	30,6
3,8	35,2
4,2	40,7
3,9	44,5
5,0	47,2
4,9	55,2
6,3	51,8
5,8	56,7

Вывод: Из диаграммы 1 видно, что связь между факторами x и y

прямая сильная линейная связь.

7.2. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами х и у.

Таблица2

№					xy
1	2,1	29,5	4,41	870,25	61,95	27,91	1,59	0,054
2	2,9	34,2	8,41	1169,64	99,18	33,46	0,74	0,022
3	3,3	30,6	10,89	936,36	100,98	36,23	-5,63	0,184
4	3,8	35,2	14,44	1239,04	133,76	39,69	-4,49	0,128
5	4,2	40,7	17,64	1656,49	170,94	42,47	-1,77	0,043
6	3,9	44,5	15,21	1980,25	173,55	40,39	4,11	0,092
7	5,0	47,2	25	2227,84	236	48,01	-0,81	0,017
8	4,9	55,2	24,01	3047,04	270,48	47,32	7,88	0,143
9	6,3	51,8	39,69	2683,24	326,34	57,02	-5,22	0,101
10	5,8	56,7	33,64	3214,89	328,86	53,55	3,15	0,056
ИТОГО:	42,2	426	193,34	19025,04	1902,04	426		0,840
Среднее зн.	4,22	42,56	19,334	1902,504	190,204

7.2.1.Проверим тесноту связи между факторами:

;

Вывод: связь сильная.

7.2.2.Проверим статистическую значимость по критерию Стьюдента:

1)Критерий Стьюдента: tвыб<=tкр

2)Н_о: r=0 tкр=2,31

tвыб=rвыб*

Вывод: таким образом поскольку tвыб=5,84<tкр=2,31, то с доверительной вероятностью

90% нулевая гипотеза отвергается, это указывает на наличие сильной линейной связи.

7.3. Полагая, что связь между факторами х и у может быть описана линейной функцией, используя процедуру метода наименьших квадратов, запишите систему нормальных уравнений относительно коэффициентов линейного уравнения регрессии. Любым способом рассчитайте эти коэффициенты.

Последовательно подставляя в уравнение регрессии из графы (2) табл.2, рассчитаем значения и заполним графу (7) табл.2

7.4. Для полученной модели связи между факторами Х и У рассчитайте среднюю ошибку аппроксимации. Сделайте предварительное заключение приемлемости полученной модели.

Для расчета заполним 8-ую и 9-ую графу табл.2

<Екр=12%

Вывод: модель следует признать удовлетворительной.

7.5. Проверьте значимость коэффициента уравнения регрессии a₁ на основе t-критерия Стьюдента.

Решение: Таблица 3

№
1	2,1	29,5	27,91	2,5281	214,623	170,5636
2	2,9	34,2	33,46	0,5476	82,81	69,8896
3	3,3	30,6	36,23	31,6969	40,069	143,0416
4	3,8	35,2	39,69	20,1601	8,237	54,1696
5	4,2	40,7	42,47	3,1329	0,008	3,4596
6	3,9	44,5	40,39	16,8921	4,709	3,7636
7	5	47,2	48,01	0,6561	29,703	21,5296
8	4,9	55,2	47,32	62,0944	22,658	159,7696
9	6,3	51,8	57,02	27,2484	209,092	85,3776
10	5,8	56,7	53,55	9,9225	120,78	199,9396
ИТОГО:	42,2	425,6	426,1	174,8791	732,687	911,504
Среднее	4,22	42,56

Статистическая проверка:

Вывод: С доверительной вероятностью 90% коэффициент a₁- статистически значим, т.е. нулевая гипотеза отвергается.

7.6. Проверьте адекватность модели (уравнения регрессии) в целом на основе F-критерия Фишера-Снедекора.

Решение:

Процедура статистической проверки:

:модель не адекватна

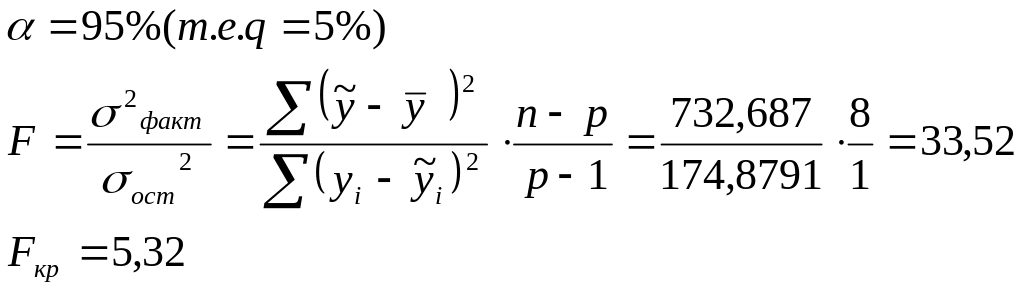
Вывод: т.к. Fвыб.>Fкр., то с доверительной вероятностью 95% нулевая гипотеза отвергается (т.е. принимается альтернативная). Изучаемая модель адекватна и может быть использована для прогнозирования и принятия управленческих решений.

7.7. Рассчитайте эмпирический коэффициент детерминации.

Решение:

(таб. 3)

-показывает долю вариации.

Вывод: т.е. 80% вариации объясняется фактором включенным в модель, а 20% не включенными в модель факторами.

7.8. Рассчитайте корреляционное отношение. Сравните полученное значение с величиной линейного коэффициента корреляции.

Решение:

Эмпирическое корреляционное отношение указывает на тесноту связи между двумя факторами для любой связи, если связь линейная, то , т.е. коэффициент корреляции совпадает с коэффициентом детерминации.

7.9. Выполните точечный прогноз для .

Решение:

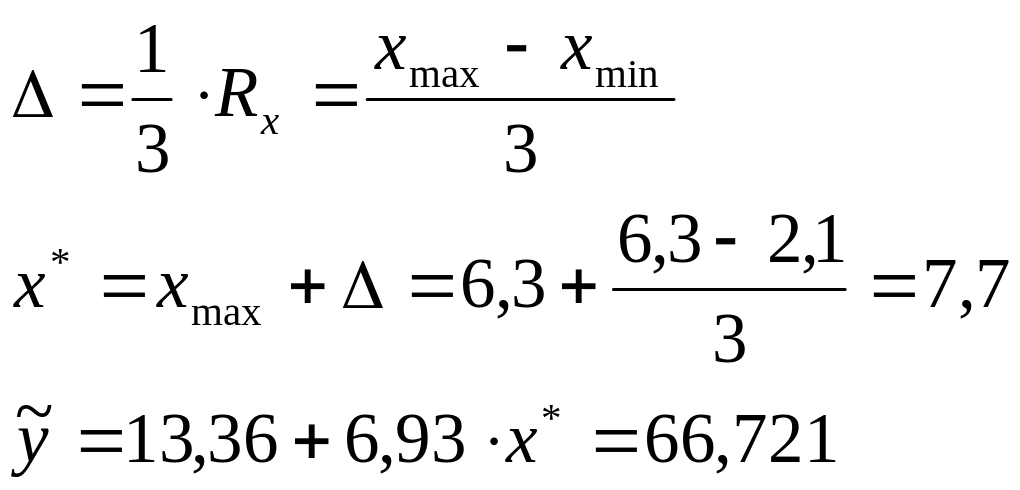
7.10-7.12. Рассчитайте доверительные интервалы для уравнения регрессии и для результирующего признака при доверительной вероятности =90%. Изобразите в одной системе координат:

а) исходные данные,

б) линию регрессии,

в) точечный прогноз,

г) 90% доверительные интервалы.

Сформулируйте общий вывод относительно полученной модели.

Решение:

-математическое ожидание среднего.

Для выполнения интервального прогноза рассматриваем две области.

1. для y из области изменения фактора x доверительные границы для линейного уравнения регрессии рассчитывается по формуле:

2. для прогнозного значения доверительный интервал для рассчитывается по формуле:

Исходные данные:

1. n=10

2. t=2,31(таб.)

3. 

4)

5) : 27,91 42,56 57,02 66,72

6) 19,334-4,22²)=1,53.

Таблица 4

№
1	2,1	-2,12	4,49	3,03	1,74	2,31	4,68	18,81	27,91	9,10	46,72
2	4,22	0,00	0,00	0,1	0,32	2,31	4,68	3,46	42,56	39,10	46,02
3	6,3	2,08	4,33	2,93	1,71	2,31	4,68	18,49	57,02	38,53	75,51
4	7,7	3,48	12,11	9,02	3	2,31	4,68	32,43	66,72	34,29	99,15

Вывод: поскольку 90% точек наблюдения попало в 90% доверительный интервал, данная модель и ее доверительные границы могут использоваться для прогнозирования с 90% доверительной вероятностью.

Задача 8. Построить линейную множественную регрессию общей суммы налогов и платежей на общую сумму поступлений по налогу на добавленную стоимость (x₁) и налогу на прибыль (доход) (x₂).

Время наблюдения	y, млрд. руб.	x1, млрд. руб.	x2, млрд. руб.
январь	38,9	5,6	13,4
февраль	45,3	6,7	15,4
март	61,1	13,1	16,7
I квартал	145,3	25,3	45,5
апрель	70,4	16,9	16,2
май	63,8	18,4	13
июнь	67,7	19,1	15
II квартал	201,9	54,4	44,2
I полугодие	347,2	79,8	89,7
июль	70,6	16,1	20,8
август	78,9	23,3	16,4
сентябрь	73,2	19,2	17,4
III квартал	222,7	58,6	54,6
9 месяцев	569,9	138,3	144,3
октябрь	78,1	16,1	23,6
ноябрь	103	31,8	23,9
декабрь	133,4	35,4	34,4
IV квартал	314,5	83,3	81,9
II полугодие	537,2	141,9	136,5
январь-декабрь	884,4	221,6	226,1

а₀=-9.7

а₁=1.84

а₂=2.62

Полученное уравнение

Задания для самостоятельной работы

1. Имеются следующие ряды оценок по тестам чтения и арифметики:

Чтение 43 58 45 53 37 58 55 61 46 64 46 62 60 56

Арифметика 32 25 28 30 22 25 22 20 20 30 21 28 34 28

Вычислите коэффициент корреляции.

2. Известны данные по числу преступлений на 100 тысяч человек, тыс. (y) в зависимости от среднедушевого дохода, тыс.руб. (x) по 10 регионам России. Построить линейную модель.

y	4,62	2,87	3,55	2,34	2,30	1,92	1,85	1,30	2,39	1,38
x	4,9	6,5	6,9	7,2	7,6	8,8	9,5	11,2	15,6	17,4

3. Дана зависимость зарплаты y, руб./мес. от стажа x, лет на некотором предприятии. Построить линейную модель.

зарплата	стаж
4 949	2
9 094	15
9 167	7
11 836	11
9 683	3
9 927	1
11 970	24
10 607	10
5 747	2
15 327	14
9 844	9
4 953	8
6 152	1
9 109	4
1 6235	7
2 621	1
13 702	12
5 771	6
15 416	9
12 035	5

4. Известна доля владельцев персональных компьютеров в зависимости от среднедушевого дохода ; объем выборки .

Логистическая модель:



Построить линейную зависимость z от х.

x	p
1	0,2	-1,386
2	0,1	-2,197
3	0,2	-1,386
4	0,3	-0,847
5	0,2	-1,386
6	0,6	0,405
7	0,4	-0,405
8	0,8	1,386
9	0,5	0
10	0,6	0,405
11	0,6	0,405
12	0,8	1,386
13	0,7	0,847
14	0,8	1,386
15	0,8	1,386
16	0,9	2,197
17	0,7	0,847
18	0,8	1,386
19	0,9	2,197
20	0,9	2,197

5. Имеются данные по 10 фирмам, продающим компакт-диски, – объемы продаж, тыс. шт. / мес. (y), цены, руб. (x₁), вложения в рекламу, тыс. руб. / мес. (x₂).

y	15	18	10	17	14	26	11	25	6	12
x1	80	100	90	75	120	85	100	70	120	75
x2	25	40	0	10	60	80	10	0	15	5

А) Построить регрессионную зависимость

Б) Проверить гипотезу о значимости коэффициентов регрессии при уровнях значимости и .

В) Построить доверительные интервалы для коэффициентов регрессии а₀, а₁, а₂ с вероятностью .

Г) Вычислить множественный коэффициент корреляции, проверить гипотезу о значимости модели при уровнях значимости и .

6. Известны данные: – цена квартиры, x₁ – общая площадь, x₂– площадь кухни.

y	x1	x2
630	30	7
640	31,5	6,2
610	31,8	5,6
980	48	7
950	46	6
1020	48,8	7,9
920	45	5,6
1050	52	7,2
1280	63	6
1310	66	6,8
1360	68	6,5
1650	72	8

А) Построить регрессионную зависимость

Б) Проверить гипотезу о значимости коэффициентов регрессии при уровнях значимости и .

В) Построить доверительные интервалы для коэффициентов регрессии а₀, а₁, а₂ с вероятностью .

Г) Вычислить множественный коэффициент корреляции, проверить гипотезу о значимости модели при уровнях значимости и .

7. Определите вид и параметры тренда в динамическом ряде: – реальный обменный курс, х – время.

год	y	х
1995	2,5	0
1996	2,3	1
1997	2	2
1998	1,7	3
1999	3,5	4
2000	3,3	5
2001	2,8	6
2002	2,4	7
2003	2,2	8
2004	2,1	9
2005	2	10

8.Определите вид и параметры тренда в динамическом ряде выплавки стали.

Год 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000

Выплавка 65,3 70,8 76,3 80,2 85,0 91,0 96,9 102,2 106,5 110,3 115,9

стали, млн.т.

9. Известен объем предложения акций на фондовом рынке в зависимости от цены. Определить лучшую регрессионную модель.

x, цена, $	y, объем, тыс.шт.
11	104
12	119
13	137
14	169
15	201
16	263
17	312
18	364
19	451
20	517

10. Имеются данные по ценам на квартиры, тыс.руб. (y) в зависимости от общей площади, м² (x₁) и площади кухни, м² (x₂).

1. Построить регрессионную зависимость

2. Обосновать наличие гетероскедастичности.

3. С помощью обобщенного метода наименьших квадратов построить зависимость с учетом гетероскедастичности.

y	995	1200	780	1150	750	1650	1880	930	2400	835
x1	46	48	30	48	31	73	88	44	73	31
x2	6	8	6	9	5	9	12	5	12	6

11. Имеются данные по странам за год.

Страна	Душевой доход, долл., y	Индекс челове­ческого развития (ИЧР),x1	Индекс челове­ческой бедности (ИЧБ), x2
Объединенные Арабские Эмираты	1600	0,866	14,9
Таиланд	7100	0,833	11,7
Уругвай	6750	0,883	11,7
Ливия	6130	0,801	18,8
Колумбия	6110	0,848	10,7
Иордания	4190	0,730	10,9
Египет	3850	0,514	34,8
Марокко	3680	0,566	41,7
Перу	3650	0,717	22,8
Шри-Ланка	3280	0,711	20,7
Филиппины	2680	0,672	17,7
Боливия	2600	0,589	22,5
Китай	2600	0,626	17,5
Зимбабве	2200	0,513	17,3
Пакистан	2150	0,445	46,8
Уганда	1370	0,328	41,3
Нигерия	1350	0,393	41,6
Индия	1350	0,446	36,7

Индекс челове­ческого развития объединяет три показателя: валовой внутренний продукт на душу населения, уровень грамотности и продолжительность жизни.

Индекс челове­ческой бедности определяется как средневзвешенное абсолютного (<1.5 $ на душу) и относительного (<3 $ на душу) индекса бедности.

Задание:

Постройте линейное уравнение множественной регрессии и пояс­ните экономический смысл его параметров.

Рассчитайте частные коэффициенты эластичности.

Определите коэффициенты регрессии.

Сделайте вывод о силе связи результата и факторов.

Определите парные коэффициенты корреляции, сделайте выводы.

Дайте оценку полученного уравнения на основе коэффициента детерминации.

12. Известны посезонные данные по объемам продаж сноубордов, шт. (y) в зависимости от цены, тыс.руб. (x). Построить линейную регрессионную модель с учетом сезонности.

	2006				2007				2008
	весна	лето	осень	зима	весна	лето	осень	зима	весна	лето	осень	зима
y	49	67	101	163	86	43	190	204	118	50	201	216
x	4,5	5	6	6,5	5	5,5	5,5	7	3,5	5	5	6

13. Даны помесячные данные о печати фотографий в некоторой фирме. Построить линейную регрессионную модель с учетом сезонности.

	месяц	y, кол-во, шт.	x1, цена, руб.	x2, рекл., руб.	x3, праздники	x4, индекс цен
1	январь, 2006	12 500	2,5	0	3	1
2	февраль	7 600	3	0	1	0,99
3	март	6 900	3	0	1	1,01
4	апрель	13 500	3	5 000	0	1,01
5	май	9 700	3	0	3	1,03
6	июнь	10 700	3	2 000	1	1,04
7	июль	12 100	3	2 000	0	1,05
8	август	9 700	3,5	2 000	0	1,03
9	сентябрь	7 000	4	2 000	0	1,05
10	октябрь	7 200	4	2 000	0	1,05
11	ноябрь	8 200	4	2 000	1	1,06
12	декабрь	8 400	4	2 000	1	1,1
13	январь, 2007	13 100	4	2 000	3	1,11
14	февраль	8 700	4	0	1	1,12
15	март	12 200	4	5 000	1	1,14
16	апрель	6 900	4	0	0	1,16
17	май	6 200	4	0	3	1,17
18	июнь	9 600	4	0	1	1,19
19	июль	8 700	4	0	0	1,18
20	август	11 900	4	4 000	0	1,18
21	сентябрь	12 600	4	6 000	0	1,2
22	октябрь	7 900	4	1 000	0	1,22
23	ноябрь	9 300	4	2 000	1	1,24
24	декабрь	11 800	4	2 000	1	1,27

14. Объем продаж мороженого (млн.шт.) за 5 лет в зависимости от цены (руб.) и сезона.

год	сезон	y, кол-во	цена	индекс цен	x, цена инд.	z(1), весна	z(2), лето	z(3), осень
2003	весна	1,5	3	1	3,00	1	0	0
	лето	2,6	4	1,11	3,60	0	1	0
	осень	1,7	3,5	1,15	3,04	0	0	1
	зима	0,9	3,5	1,26	2,78	0	0	0
2004	весна	1,4	4	1,34	2,99	1	0	0
	лето	3	4	1,40	2,86	0	1	0
	осень	2,8	4	1,45	2,76	0	0	1
	зима	1,6	4	1,52	2,63	0	0	0
2005	весна	1,9	4,5	1,59	2,83	1	0	0
	лето	3,2	5	1,63	3,07	0	1	0
	осень	2,7	4,5	1,68	2,68	0	0	1
	зима	2	4,5	1,78	2,53	0	0	0
2006	весна	2,2	5	1,87	2,67	1	0	0
	лето	3,4	5	1,95	2,56	0	1	0
	осень	2,6	5	2,01	2,49	0	0	1
	зима	2,1	5	2,09	2,39	0	0	0
2007	весна	2,9	5	2,16	2,31	1	0	0
	лето	3,3	6	2.19	2,74	0	1	0
	осень	2,5	6	2,24	2,68	0	0	1
	зима	2,2	6	2,32	2,59	0	0	0

15. Изучается влияние стоимости основных и оборотных средств на величину валового дохода торговых предприятий.

Для этого по 12 торговым предприятиям были получены следующие данные.

Номер предприятия	Валовой доход за год, млн. руб.	Среднегодовая стоимость, млн. руб.
		основных фондов	оборотных средств
1	203	118	105
2	63	28	56
3	45	17	54
4	113	50	63
5	121	56	28
6	88	102	50
7	110	126	54
8	56	124	42
9	80	114	36
10	237	154	106
11	160	115	88
12	75	98	46

Задание:

Постройте линейное уравнение множественной регрессии и пояс­ните экономический смысл его параметров.

Рассчитайте частные коэффициенты эластичности.

Определите коэффициенты регрессии.

Сделайте вывод о силе связи результата и факторов.

Определите парные коэффициенты корреляции, а также множественный коэффициент корреляции; сделайте выводы.

Дайте оценку полученного уравнения на основе коэффициента детерминации.

16. Имеются данные о деятельности крупнейших компаний США в 2006г.

№ п/п	Чистый доход, млрд долл.США, у	Оборот капитала, млрд долл. США, х1	Использованный капитал, млрд долл. США, х2	Числен­ность служа­щих, тыс.чел., х3	Рыночная капитали-зация компании, млрд долл. США, х4
1	0,9	31,3	18,9	43,0	40,9
2	1,7	13,4	13,7	64,7	40,5
3	0,7	4,5	18,5	24,0	38,9
4	1,7	10,0	4,8	50,2	38,5
5	2,6	20,0	21,8	106,0	37,3
6	1,3	15,0	5,8	96,6	26,5
7	4,1	137,1	99,0	347,0	37,0
8	1,6	17,9	20,1	85,6	36,8
9	6,9	165,4	60,6	745,0	36,3
10	0,4	2,0	1,4	4,1	35,3
11	1,3	6,8	8,0	26,8	35,3
12	1,9	27,1	18,9	42,7	35,0
13	1,9	13,4	13,2	61,8	26,2
14	1,4	9,8	12,6	212,0	33,1
15	0,4	19,5	12,2	105,0	32,7
16	0,8	6,8	3,2	33,5	32,1
17	1,8	27,0	13,0	142,0	30,5
18	0,9	12,4	6,9	96,0	29,8
19	1,1	17,7	15,0	140,0	25,4
20	1,9	12,7	11,9	59,3	29,3
21	-0,9	21,4	1,6	131,0	29,2
22	1,3	13,5	8,6	70,7	29,2
23	2,0	13,4	11,5	65,4	29,1
24	0,6	4,2	1,9	23,1	27,9
25	0,7	15,5	5.8	80,8	27,2

Задание:

Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.

Дайте сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности.

Рассчитайте матрицы парных коэффициентов корреляции и на их основе отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.

Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.

Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (γ = 0,05; γ = 0,10).

17. Имеются данные о деятельности крупнейших компаний США в 2006г.

№ п/п	Чистый доход, млрд долл. у	Оборот капи­тала, млрд долл. США, х1	Использованный капитал, млрд долл. х2	Численность, тыс. чел., х3
1	6,6	6,9	83,6	222,0
2	3,0	18.0	6,5	32,0
3	6,5	107,9	50,4	82,0
4	3,3	16,7	15,4	45,2
5	0,1	79,6	29,6	299,3
6	3,6	16,2	13,3	41,6
7	1,5	5,9	5,9	17,8
8	5,5	53,1	27,1	151,0
9	2,4	18,8	11,2	82,3
10	3,0	35,3	16,4	103,0
11	4,2	71,9	32,5	225,4
12	2,7	93,6	25,4	675,0
13	1,6	10,0	6,4	43,8
14	2,4	31,5	12,5	102,3
15	3,3	36,7	14,3	105,0
16	1,8	13,8	6,5	49,1
17	2,4	64,8	22,7	50,4
18	1,6	30,4	15,8	480,0
19	1,4	12,1	9,3	71,0
20	0,9	31,3	18,9	43,0

Задание:

Рассчитайте параметры линейного уравнения множественной рег­рессии с полным перечнем факторов.

Дайте сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности.

Рассчитайте матрицы парных и частных коэффициентов корреляции и на их основе отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.

Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.

Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а = 0,10).

Оцените полученные результаты, выводы оформите в аналитической записке.