3. Линейная модель множественной регрессии

3.1. Обоснование и отбор факторов при построении множественной регрессии.

Значения экономических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. Задача оценки статистической взаимосвязи переменных у и х=(х₁,х₂,…,х_m) формулируется аналогично случаю парной регрессии. Ищется функция у=f(,х)+, где – вектор параметров, – случайная ошибка.

Построение функции проводится в два этапа.

На первом этапе необходимо произвести отбор факторов. Сначала вычисляются коэффициенты корреляции r_ik по формуле (3) между выборочными значениями факторов Х_i={x_ji} и Х_k={x_jk}. Если r_ik>0.8 (наблюдается сильная линейная связь между факторами Х_i и Х_k), то один из них отбрасывается (в принципе, любой, но рекомендуется отбрасывать тот, информацию по которому труднее собрать или она менее достоверна). Затем вычисляются коэффициенты корреляции r_iу по формуле (3) между выборочными значениями фактора Х_i={x_ji} и Y={y_j}. Если r_iy<0.2 (практически отсутствует линейная связь между фактором Х_i и анализируемым показателем Y), то и этот фактор отбрасывается.

3.2. Линейная регрессионная модель со многими переменными.

В простейшем случае анализируется линейная зависимость у от х. Уравнение множественной линейной регрессии имеет вид

у=₀+₁х₁ +₂х₂ +…+_mх_m+. (12)

Если имеется n наблюдений факторов х и переменной у, то отклонение зависимой переменной у в j-м наблюдении от линии регрессии

_j= у_j – ₀ – ₁х_j1 – ₂х_j2 – … – _mх_jm (j=1,2,…, n).

На втором этапе для оставшихся факторов применяется метод наименьших квадратов. Метод наименьших квадратов предполагает поиск коэффициентов _i таких, что Q=_j²min. Для отыскания минимума берутся частные производные Q по искомым параметрам (мы использовали этот метод в случае однофакторной регрессии для нахождения ₀ и ₁) и приравниваются к нулю. После выполнения элементарных преобразований получают так называемую систему нормальных уравнений, из которой и находятся искомые параметры.

Система нормальных уравнений для многофакторной регрессии имеет вид:

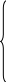 ₀ + _{1 1} + _{2 2} + … + _{m m} = ,

_{0 1} + ₁ + ₂ + … + _m = , (13)

……………………………………………..

₀ + ₁ + ₂ + … + _m = .

Для решения системы (13) можно использовать любой метод решения системы линейных уравнений (Гаусса, Крамера и пр.). Оцененное уравнение описывает как общий тренд (тенденцию) изменения зависимой переменной у, так и отклонения от этого тренда. Проблема здесь состоит не только в том, чтобы объяснить возможно большую долю колебаний переменной у, но и отделить влияние каждого из факторов.

3.3. Оценка и интерпретация параметров.

Для анализа статистической значимости полученных коэффициентов множественной линейной регрессии оценивают дисперсию D(_i) и стандартные отклонения S(_i)=D(_i) коэффициентов _i. Аналогично (10) величина t=_i/S(_i), называемая t–статистикой, имеет распределение Стьюдента с (n-m-1) степенями свободы. Если число степеней свободы достаточно велико (не менее 10), то при 5%-ном уровне значимости можно приближенно считать оценку незначимой, если t–статистика по модулю меньше 1, и весьма надежной, если модуль t–статистики больше 3.

Коэффициенты множественной линейной регрессии _i имеют большой экономический смысл. Они показывают, на сколько изменится анализируемый показатель Y при изменении фактора Х_i на единицу.

Пример 3. Рассмотрим аналитические модели спроса, используя ниже приведенные в табл.3 конкретные статистические данные обследования семей, сведенные в девять групп (с примерно одинаковым объемом потребления).

Таблица 3.

№ группы	Расход на питание (у)	Душевой доход (х1)	Размер семей (х2)	ŷ	j	j2
1	2	3	4	5	6	7
1	433	628	1,5	333,6	99,4	9880,36
2	616	1577	2,1	626,5	–10,5	110,25
3	900	2659	2,7	928,5	–28,5	812,25
4	1113	3701	3,2	1189,8	–76,8	5898,24
5	1305	4796	3,4	1340,5	–34,5	1190,25
6	1488	5926	3,6	1493,6	–5,6	31,36
7	1645	7281	3,7	1624	21	441
8	1914	9350	4,0	1879,1	34,9	1218
9	2411	18807	3,7	2409,5	1,5	2,25
Средние	=1313,9	1 =6080,5	2 =3,1			2198,2

Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода (х₁)

ŷ =а₀ + а₁х₁,

параметры которой а₀ и а₁ находятся по формулам (6), используя данные табл.3 и =(∑х₁²)/9=63989644,1, =(∑х₁у)/9)=10894351. Решение: а₀=660,06; а₁ = 0,1075. Получаем уравнение регрессии ŷ =660,06 + 0,1075х₁.

Затем вычисляются средняя квадратическая ошибка выборки (корень квадратный из дисперсии у)

S_у=√(∑(у – у)²)/n,

с редняя квадратическая ошибка уравнения (4) S_ŷ =√(∑(у – ŷ)²)/n и коэффициент детерминации R_ŷх1 =√1 – S_ŷ²/ S_у².

В нашем примере S_у²=454070, S_ŷ²=63846, следовательно

R_ŷх1 =√1 – 63846/454070 =0,927.

Полученное значение свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.

Величина R²_ŷх1 показывает долю изменения результативного признака под воздействием факторного признака. В нашем примере R²_ŷх1 =0,859; это означает, что фактором душевого дохода можно объяснить почти 86% изменения расходов на питание.

Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода (х₁) и размера семьи (х₂)

ŷ =а₀ + а₁х₁ + а₂х₂ .

Параметры модели а₀ , а₁ и а₂ находятся посредством решения следующей системы нормальных уравнений:

а₀ + х₁а₁ + х₂а₂ = у

х₁а₀ + а₁ + х₁х₂ а₂ = ух₁

х₂а₀ + х₁х₂ а₁ + а₂ = ух₂,

к оторая также формируется с применением метода наименьших квадратов (средние величины х₁х₂ , и ух₂ вычисляются аналогично однофакторной модели). Получаем систему

а₀ + 6080,5а₁ + 3,1а₂ = 1313,9

6080,5а₀ + 63989644,1а₁ + 21649,1 а₂ = 10894351

3,1а₀ + 21649,1а₁ + 10,2а₂ = 4488,

которую решаем, например, методом Гаусса.

Делим второе и третье уравнения на коэффициент при а₀.

а₀ + 6080,5а₁ + 3,1а₂ = 1313,9

а₀ + 10523,75а₁ + 3,56 а₂ = 1791,69

а₀ + 6983,58а₁ + 3,29а₂ = 1447,74.

От второго и третьего уравнения отнимаем первое

а₀ + 6080,5а₁ + 3,1а₂ = 1313,9

4443,25а₁ + 0,46 а₂ = 477,79

903,08а₁ + 0,19а₂ = 133,84.

Делим второе и третье уравнения на коэффициент при а₁.

а₀ + 6080,5а₁ + 3,1а₂ = 1313,9

а₁ + 0,0001035 а₂ = 0,1075316

а₁ + 0,0002104а₂ = 0,1482039.

От третьего уравнения отнимаем второе

а₀ + 6080,5а₁ + 3,1а₂ = 1313,9

а₁ + 0,0001035 а₂ = 0,1075316

0,0001069а₂ = 0,0406723.

Из третьего уравнения находим а₂ =380.47; подставляя его во второе уравнение получаем а₁ = 0,06815; подставляя найденные а₁ и а₂ в первое уравнение, получаем а₀ = –279.94; следовательно

ŷ = –279.94 + 0.06815х₁ + 380.47х₂ .

Для определения тесноты связи предварительно вычисляются теоретические значения ŷ, затем уклонения _j и их квадраты (колонки 5,6,7 табл.3). Получим S_ŷ² =(∑(у – ŷ)²)/n =2198,2. Используя ранее вычисленное S_у²=454070, получим R² =1 – S_ŷ²/ S_у² =0,995. R² показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. У нас R²=0,995; это означает, что совместное влияние душевого дохода и размера семей объясняет почти 99,5% изменения расходов на питание.