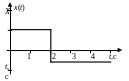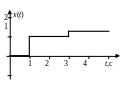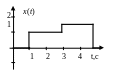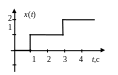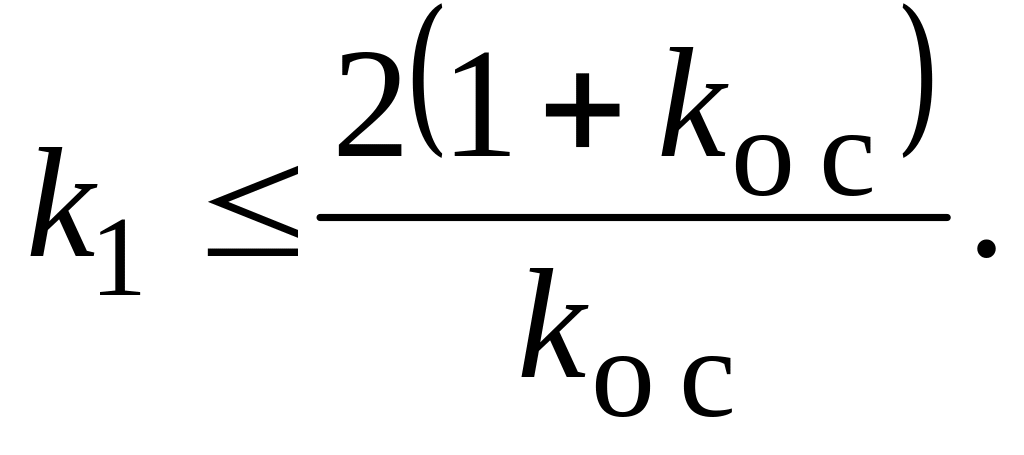Задания

1. Определить установившееся значение выходной координаты, используя уравнение статики элемента.

2. Записать характеристическое уравнение и найти его корни.

3. По значениям действительной и мнимой составляющей корня определить: устойчивый или неустойчивый процесс. Если процесс устойчивый, то рассчитать время затухания процесса и частоту собственных колебаний. Если процесс неустойчивый, определить частоту собственных колебаний и построить первые два периода.

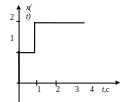
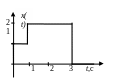
4. Представить график реакции элемента на изменение входного сигнала.

В табл. 2 даны варианты заданий, вид воздействия и тип исследуемого звена.

Таблица 1. Варианты заданий

(уравнения динамики звеньев даны в приложении)

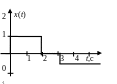
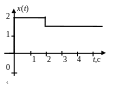
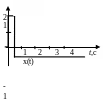
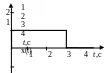
№ вар.	Тип звена	Параметры звена	Вид воздействия
0	Инерционно- дифференцирующее
1	Инерционно- дифференцирующее

Продолжение табл. 2

№ вар.	Тип звена	Параметры звена	Вид воздействия
2	Интегрирующее	T = 1
3	Интегрирующее	T = 0,5
4	Инерционное (апериодическое 1-го порядка)	k =10 T =3
5	Инерционное (апериодическое 1-го порядка)	k =2 T =0,5

Окончание табл. 2

№ вар.	Тип звена	Параметры звена	Вид воздействия
6	Апериодическое 2-го порядка	k = 2 = 1 T2 = 2
7	Апериодическое 2-го порядка	k = 1 = 16 T2 = 8
8	Колебательное	k = 2 = 1 T2 = 1
9	Колебательное	k = 2 = 2 T2 = 2

Тема 3. Нахождения области допустимого

сочетания параметров, обеспечивающих

устойчивость системы

Пример 1

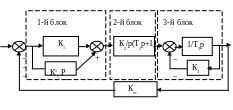
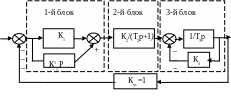
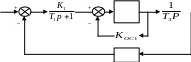
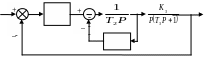
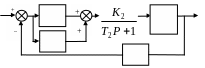
На рис. 5 дана структурная схема системы и значения параметров звеньев (k_i, T_i ).

Рис. 5. Структурная схема системы управления

Требуется определить область устойчивости системы (или область отсутствия собственных колебаний в системе, если порядок характеристического уравнения n < 3) в плоскости параметров x1 – x2 методом Раусса – Гурвица.

В данном примере область устойчивости определяется в плоскости параметров К₁ и К_ос , т.е. x1 = К₁, x2 = К_ос, остальные приняты равными 1.

Решение

1. Запишем передаточную функцию 1-го блока (параллельное соединение элементов):

2. Запишем передаточную функцию 3-го блока (элемент охвачен отрицательной обратной связью):

.

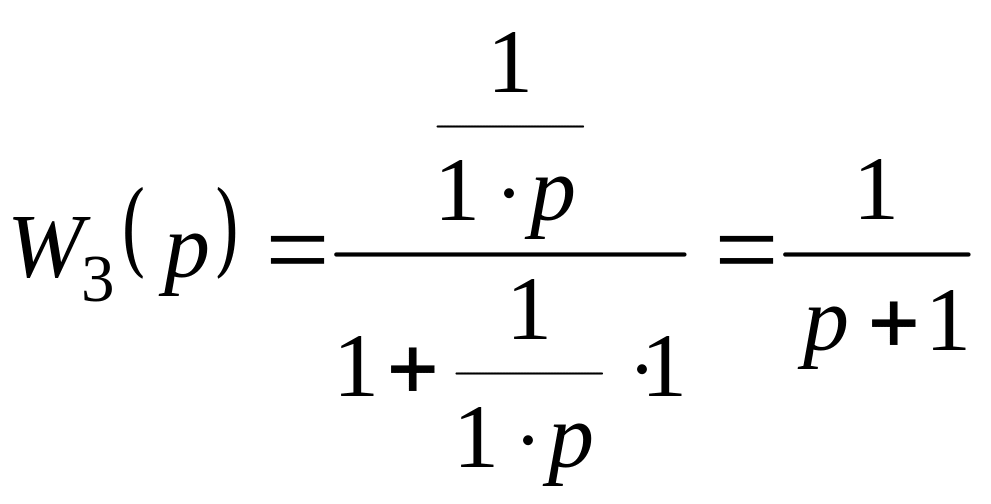3. Запишем передаточную функцию трех последовательно соединённых блока – :

.

4. Запишем выражение для расчёта передаточной функции замкнутой системы

.

5. В выражение для вывода характеристического уравнения замкнутой системы

подставим значения передаточных функций:

.

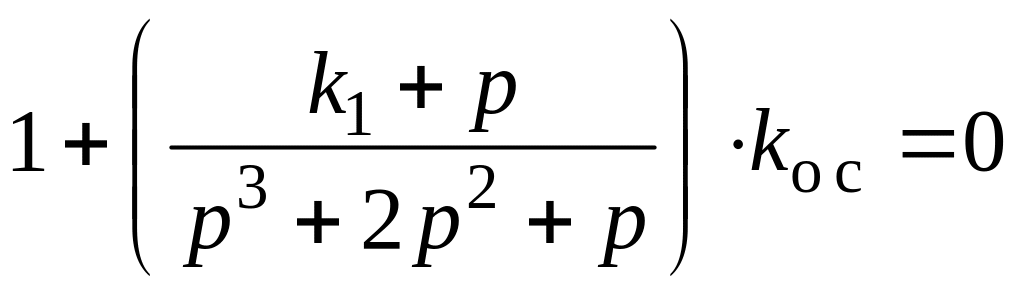6. Приведём дробь к общему знаменателю и приравняем числитель к нулю:

,

(1)

где

7. Запишем необходимое условие устойчивости по критерию Раусса – Гурвица:

все , ( i = 0,1,2,…n, для рассматриваемого случая n = 3).

Для уравнения (1) имеем

, при любых значениях К₁ и К_{о с} ,

, при любых К₁ и К_{о с} ,

, при ,

при и ,

или , .

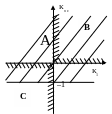
На рис. 6, 7 построены границы области устойчивости, удовлетворяющие необходимым условиям критерия.

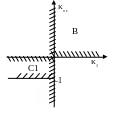
Рис. 6. Области, где выполняются условия: а2 > 0 (область А) и а3 > 0 (области В и С)	Рис. 7. Области, удовлетворяющие необходимым условиям Раусса – Гурвица

8. Запишем достаточное условие критерия Раусса – Гурвица. В найденных областях В и С1 для уравнения 3-го порядка достаточным условием является положительность определителя Гурвица, составленного из коэффициентов а_i характеристического уравнения:

, т.е.

(2)

Подставив значения в (2), имеем:

(3)

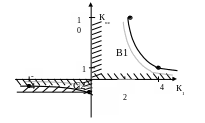
Равенство левой и правой частей даёт уравнение границы, а знак “≤” – допустимую область сочетания параметров (рис. 8).

Рис. 8. В1 и С2 – области допустимого сочетания параметров, внутри которых выполняются необходимые и достаточные условия устойчивости

Пример 2

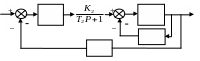
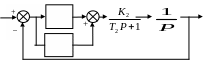
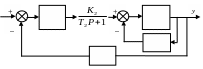
На рис. 9 дана структурная схема системы.

Требуется найти область допустимых значений параметров x1 – x2, при которых система устойчивая и собственные движения системы носят апериодический (неколебательный) характер (рис. 9).

Рис. 9. Структурная схема системы

Решение

1. Запишем передаточную функцию 1-го блока (параллельное соединение звеньев):

.

2. Запишем передаточную функцию 3-го блока (элемент, охваченный отрицательной обратной связью):

.

3. Запишем передаточную функцию трёх последовательно соединённых блоков:

.

4. Запишем выражение для расчёта передаточной функции замкнутой системы

.

5. В выражение для вывода характеристического уравнения замкнутой системы

подставим значения передаточных функций:

(1)

6. Выделим искомые параметры х1 и х2, остальные положим равными 1. Допустим , . Для этого случая уравнение (1) примет вид:

(2)

7. Уравнение (2), приведя к общему знаменателю и приравняв числитель дроби к нулю, приведём к виду:

, , , , .

(3)

Для оценки устойчивости системы, когда характеристическое уравнение имеет порядок < 3, достаточно проверить выполнение необходимого условия критерия Раусса – Гурвица, т.е. все коэффициенты должны быть > 0. Для рассматриваемого случая это условие выполняется, если

(4)

Границы допустимой области показаны на рис. 10.

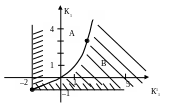
Рис. 10. Границы допустимой области

8. Колебательность системы определяется по наличию комплексных корней характеристического уравнения:

.

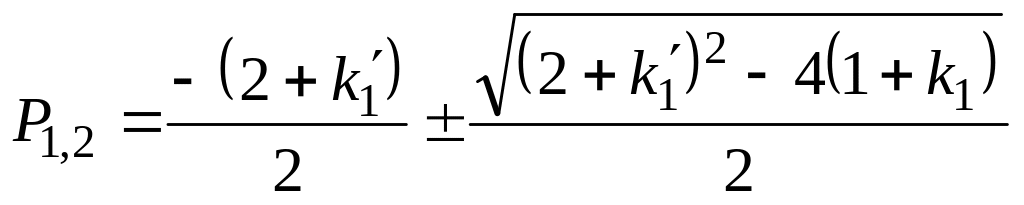Корень будет иметь мнимую составляющую (а система будет склонна к колебаниям), если дискриминант (подкоренное выражение) меньше нуля.

9. Запишем условие отсутствия колебаний:

(5)

При равенстве левой и правой части получим уравнение для построения границы области отсутствия колебаний.

10. Решим уравнение (5) относительно параметра, например, k₁.

.

(6)

Графическое решение уравнения (6) с учетом (4) дает область отсутствия колебаний (B) в области устойчивости системы (A).

Задания

1. Построить области устойчивости в плоскости двух параметров х1 – х2 (табл. 3).

Примечание: если порядок характеристического уравнения n = 2, то находить и область устойчивости, и область отсутствия колебаний, если n = 3, то только область устойчивости.

Для курсовых работ студентов заочного отделения.

2. Зафиксировав один из параметров, например Х1, построить область устойчивости в плоскости 1-го параметра – Х2.

Таблица 3. Варианты задания, изменяемые параметры х1 – х2

и структурные схемы

№ вар-та и пара-метры х1–х2	Структурная схема системы
0 к1 –кос1

Продолжение табл. 3

№ вар-та и пара-метры х1–х2	Структурная схема системы
1 к3 – к4
2 к1 – кос
3 к1 – к3
4 к1 – к2
5 к2 –Т2

Окончание табл. 3

№ вар-та и пара-метры х1–х2	Структурная схема системы
6 к1 – к3
7 к1 –кос
8 к2 –Т3
9 к3 – к4