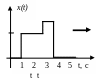Задания

1. Записать характеристическое уравнение системы и найти корни уравнения.

2. По значениям действительной и мнимой составляющей корня определить: устойчивый или неустойчивый процесс, если процесс устойчивый, рассчитать время затухания процесса и частоту собственных колебаний. Если процесс неустойчивый, определить частоту собственных колебаний и построить первые два периода.

3. Представить график собственных движений элементов системы.

Таблица 1. Значение коэффициентов модели и начальных условий y(0) и dy(0)/dt

№ варианта			y(0)	dy/dt
0	1	1,4	1	1
1	1	0,9	–1	1
2	1	0,5	1	1
3	1	–1,4	–1	1
4	1	–0,9	1	1
5	1	–0,5	–1	1
6	0,1	1,4	1	1
7	0,1	0,9	–1	1
8	0,1	–1,4	1	1
9	0,1	–0,9	–1	1

Тема 2. Оценка вида вынужденных

движений системы (элемента системы)

Пример.

Дано: дифференциальное уравнение типового звена и нулевые начальные условия:

(1)

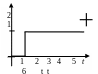
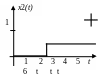
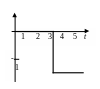
Примечание. Входной сигнал x(t) имеет сложную форму, которую можно считать суммой единичных ступенек х1 + х2 + х3, например:

2 1	x1(t)
	x3(t)

В рассматриваемом примере изменения входного воздействия x(t) возникают в моменты времени t = 0 и t = 4 c.

Требуется представить качественный вид реакции звена на изменение входного сигнала: 1) оценить установившееся значение выходного сигнала; 2) определить длительность переходного процесса; 3) определить количество колебаний за время переходного процесса.

Решение. Для линейной системы справедлив принцип суммирования реакций на входные воздействия, т. е. y(t) = y1(t) + y2(t), где y1(t) – реакция на x1, а на x2.

Запишем уравнения динамики для каждого из воздействий. Допустим, звено имеет следующие параметры (причем чувствительность к воздействиям у звена разная):

;

и .

Оценим установившееся значение выходной координаты. Для устойчивых линейных систем справедливо утверждение:

Таким образом, уравнения статики (y_т(t)|_t→∞) примет вид

Установившееся значение выходной координаты:

.

Оценим длительность переходного процесса – реакции на каждое из воздействий. Длительность процесса (как и длительность собственных движений системы) определяется по величине реальной части корней характеристического уравнения. Таким образом, определив корни характеристического уравнения, мы сможем оценить длительность переходного процесса (t_пп.) и количество колебаний за t_пп. Запишем дифференциальное уравнение собственных движений, для этого приравняем правую часть уравнения (1) к нулю:

.

(2)

Характеристическое уравнение:

.

(3)

Корни характеристического уравнения:

Время затухания процесса определяется реальной частью , а частота колебаний – мнимой частью корня Так как решение уравнения (2) записывается в виде

то огибающая функции C₁sin(0,6 ∙ t + С₂) определяется затухающей экспонентой . Если учесть, что , то можно оценить длительность процесса затухания собственных движений системы t_пп. Это произойдет приблизительно через 4,5 с после появления отклонения y(t) от исходного принятого за ноль значения. Так как второе воздействие возникло при t = 4 с, то к моменту t ≈ 8,5 с переходные процессы закончатся. Таким образом, t_пп ≈ 8,5 с.

Оценим колебательность процесса. Если величина действительной части комплексного корня характеризует скорость затухания (расхождения) процесса, то величина мнимой части определяет частоту собственных колебаний – ω.

Так как реакции, как на первое, так и второе воздействия, длятся 4,5 с, то за время реакции можно наблюдать приблизительно полпериода собственных колебаний (рис. 3, 4).

x1 x2

y(t)

y1(t)

y2(t)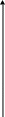

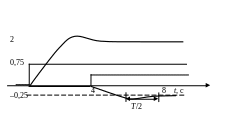
Рис. 3. Компоненты вынужденных движений

Общая реакция: y(t) = y1(t) + y2(t)

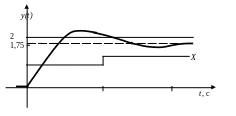
Рис. 4. Общий вид вынужденных движений