Федеральное агентство морского и речного транспорта
Федеральное государственное образовательное учреждение
высшего профессионального образования
«Волжская государственная академия водного транспорта»
Кафедра информатики, систем управления
и телекоммуникаций
Серия «Информационные технологии
в системах управления и телекоммуникаций»
Выпуск 3
М.М. Чиркова
Сборник тестовых задач
по теории автоматического управления
Методическое пособие
для студентов очного и заочного обучения
технических специальностей
Ответственный редактор – Ю.С. Федосенко
Нижний Новгород
Издательство ФГОУ ВПО «ВГАВТ»
2010
УДК 681.5
Ч64
Редакционная коллегия серии «Информационные технологии в системах управления и телекоммуникаций»:
Ю.С. Федосенко – д.т.н., профессор;
М.М. Чиркова – д.т.н., профессор;
В.И. Логинов – к.т.н., доцент;
А.В. Преображенский – к.т.н., доцент
Чиркова, М.М.
Сборник тестовых задач по теории автоматического управления : метод. пособие для студ. оч. и заоч. обучения технич. специальностей / М.М. Чиркова ; отв. ред. Ю.С. Федосенко. – Н. Новгород : Изд-во ФГОУ ВПО «ВГАВТ», 2010. – 32 с.
Изложены примеры решения задач по основным темам теории автоматического управления (линейные системы). Пособие может быть использовано при проведении практических занятий, контрольных работ, тестовых опросах студентов.
Для студентов технических специальностей дневного и заочного обучения.
Работа рекомендована к изданию кафедрой информатики, систем управления и телекоммуникаций (протокол № 5 от 21.05.2009 г.).
© ФГОУ ВПО «ВГАВТ», 2010
Введение
Навык решения задач по теории автоматического управления необходим для более глубокого понимания материала, излагаемого в лекционном курсе ТАУ. Нельзя проектировать систему управления состоянием технического объекта, не прибегая к моделированию динамики системы и её элементов с использованием их математических моделей (уравнений динамики). Основные вопросы, которые решаются с помощью моделей: построение статических и динамических характеристик элементов, узлов, системы; построение областей устойчивости в области тех параметров регулятора, выбор которых (или перенастройка в процессе эксплуатации) возможен на этапе проектирования. Под собственными параметрами понимают коэффициенты передачи (ki), инерционные свойства элементов системы (Ti).
При расчетах исходным является уравнение динамики вынужденных движений системы (элемента, узла), связывающее координаты состояния yi и их производные dyi/dt, d2yi/dt2, … (иногда их не очень удачно называют «переменные параметры») с собственными параметрами системы (ki, Ti,) и с внешними воздействиями X(t) (1). Внешние воздействия подразделяют на два типа – задающие, или управляющие, и возмущающие. Для первого типа воздействий обычно используют обозначения U или Y0. Для второго типа – F (отражает состояние внешней среды, влияющей на работу объекта управления) или N (нагрузка, подключенная к объекту, например, ток нагрузки на шинах генератора).
(1)
где n – порядок дифференциального уравнения. Высокий порядок уравнения (n > 3) не только усложняет расчеты, но и указывает на сложную динамику системы. Полное уравнение динамики (1), когда Х(t) ≠ 0 (правая часть уравнения (1)), используют для построения как статических характеристик системы, так и вынужденных движений системы.
Для построения статических характеристик, что возможно только после оценки устойчивости системы (способности возвращаться в исходное состояние после кратковременного воздействия помех), используют уравнение статики, когда все производные координаты состояния в уравнении (1) зануляют:
,
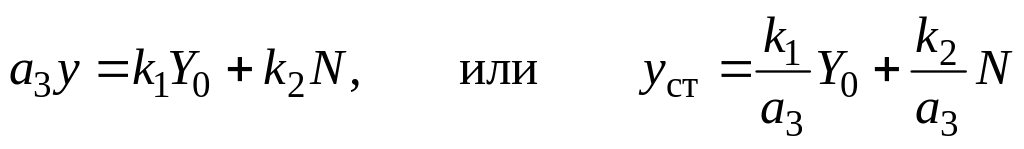(2)
где ycт – установившееся (статическое) значение координаты состояния;
k1/a3 – коэффициент чувствительности к задающему (или управляющему) воздействию;
k2/a3 – коэффициент чувствительности к нагрузке (или изменению состояния внешней среды).
В том случае, когда реакция каждого элемента системы прямо пропорциональна воздействию и реакция на сумму воздействий равна сумме реакции на каждое воздействие, систему называют линейной. Полученное выше уравнение статики справедливо для линейных устойчивых систем.
Динамику линейных систем проще оценить по собственным движениям системы – возврат в исходное состояние после кратковременного изменения какого-либо из воздействий (F, N). В этом случае используют уравнение собственных движений системы, (когда в (1) Х(t) = 0), и отличные от нуля начальные условия – отклонения координат состояния от исходного значения, которое возникло из-за кратковременного воздействия помехи.
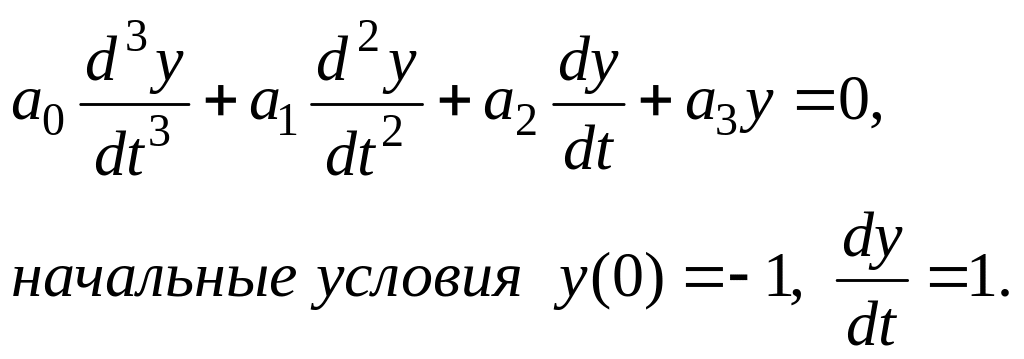(3)
Уравнение собственных движений системы (3) необходимо для получения характеристического уравнения (4) и расчета его корней.
|
(4) |
,
.
Вид корней (действительные или комплексные) и значение действительной и мнимой составляющей зависят от собственных параметров (ki, Ti) и полностью определяют характер (динамику) устройства: носят ли процессы в устройстве колебательный характер или апериодический, как быстро затухают процессы и затухают ли они вообще.
В данном пособии рассматривается несколько типов задач, решение которых отвечает на поставленные вопросы.