
- •Введение
- •1 Обзор существующих мехатронных модулей
- •Классификация мехатронных модулей движения
- •Общая информация и технические характеристики существующих мехатронных модулей движения
- •2.1.2 Расчет геометрических параметров гайки шарико-винтовой передачи
- •2.1.3 Проверочный расчет передачи по контактным напряжениям
- •2.1.4 Проверка винта на статическую устойчивость
- •2.1.5 Проверка винта на динамическую устойчивость
- •2.2 Расчет требуемой мощности двигателя мехатронного модуля
- •2.3 Определение главных размеров статора и ротора асинхронного двигателя
2.1.2 Расчет геометрических параметров гайки шарико-винтовой передачи
Смещение профиля резьбы в радиальном направлении:
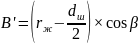 (2.19)
(2.19)
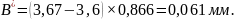
Внутренний диаметр гайки:
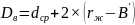 (2.20)
(2.20)
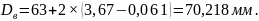
Диаметр окружности, по которой происходит контакт шариков с гайкой:
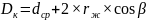 (2.21)
(2.21)
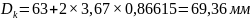
Внешний диаметр гайки:
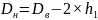 (2.22)
(2.22)
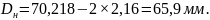
Наружный диаметр гайки при расположении в ней возвратного канала:
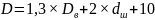 (2.23)
(2.23)
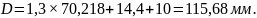
Наружный диаметр гайки при расположении возвратного канала вне гайки, мм:
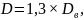
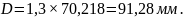
2.1.3 Проверочный расчет передачи по контактным напряжениям
Условие контактной прочности:
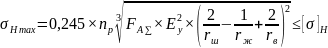 , (2.24)
, (2.24)
где
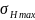 – максимальные контактные напряжения,
МПа;
– максимальные контактные напряжения,
МПа;
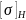 – допускаемые
контактные напряжения, МПа (для
винтовых поверхностей винта и гайки
твердостью HRC≥ 53 и шариков твердостью
HRC ≥ 63 допускаемые контактные напряжения
равны
= 3500…5000 МПа);
– допускаемые
контактные напряжения, МПа (для
винтовых поверхностей винта и гайки
твердостью HRC≥ 53 и шариков твердостью
HRC ≥ 63 допускаемые контактные напряжения
равны
= 3500…5000 МПа);
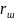 – радиус
шарика,
– радиус
шарика,
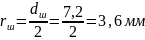 ;
;
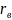 – внутренний
радиус винта,
– внутренний
радиус винта,
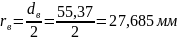 ;
;
– модуль
упругости первого рода,
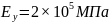 ;
;
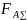 –
суммарная
осевая сила;
–
суммарная
осевая сила;
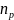 – коэффициент
нагрузки, определяемый в зависимости
от отношения главных кривизн А/Д по
таблице 2.1.
– коэффициент
нагрузки, определяемый в зависимости
от отношения главных кривизн А/Д по
таблице 2.1.
Суммарная осевая сила определяется по формуле:
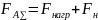 , (2.25)
, (2.25)
где
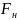 – сила предварительного натяга,
– сила предварительного натяга,
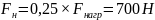 .
.
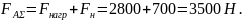
Главная кривизна в плоскости наиболее плотного касания:
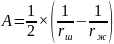 (2.26)
(2.26)
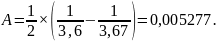
Главная кривизна в плоскости наименее плотного касания:
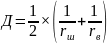 (2.27)
(2.27)
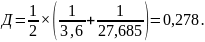
А/Д=0,01898.
Таблица 2.1 – Значения коэффициента нагрузки
А/Д |
|
А/Д |
|
А/Д |
|
1,0000 |
1,0000 |
0,2967 |
0,9262 |
0,05797 |
0,7144 |
0,8459 |
0,9985 |
0,2501 |
0,9067 |
0,04237 |
0,6740 |
0,6816 |
0,9919 |
0,2004 |
0,8766 |
0,02962 |
0,6300 |
0,5022 |
0,9746 |
0,1462 |
0,8386 |
0,01787 |
0,5721 |
0,3410 |
0,9409 |
0,09287 |
0,7774 |
0,00385 |
0,4267 |
Исходя из соотношения А/Д по таблице 1 определяем nр=0,6300.
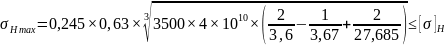
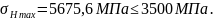 ,
следовательно, расчет верен.
,
следовательно, расчет верен.
2.1.4 Проверка винта на статическую устойчивость
Винты передачи подвержены воздействию значительной осевой силы. В зависимости от схемы осевой фиксации вращающиеся винты работают на растяжение или сжатие.
Вычисляют значение критической силы Fкр, Н, по Эйлеру:
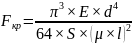 , (2.28)
, (2.28)
где
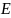 –
модуль упругости материала винта,
–
модуль упругости материала винта,
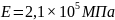 ;
;
 – диаметр
резьбы винта по впадинам,
– диаметр
резьбы винта по впадинам,
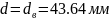 ;
;
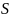 – коэффициент
запаса,
– коэффициент
запаса,
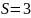 ;
;
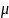 – коэффициент,
зависящий от способа закрепления винта,
для случая, когда оба конца заделаны
жестко
– коэффициент,
зависящий от способа закрепления винта,
для случая, когда оба конца заделаны
жестко
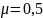 ;
;
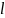 – длина
нагруженного (неопорного) участка винта,
– длина
нагруженного (неопорного) участка винта,
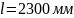 .
.
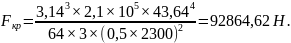
Условие статической устойчивости:
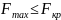 , (2.29)
, (2.29)
где
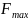 – наибольшая осевая сила, нагружающая
винт на длине
,
– наибольшая осевая сила, нагружающая
винт на длине
,
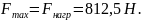
Так
как
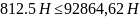 то статическая устойчивость обеспечена.
то статическая устойчивость обеспечена.
2.1.5 Проверка винта на динамическую устойчивость
Частота вращения находится в допустимых пределах при выполнении условия
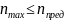 , (2.30)
, (2.30)
где
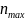 – наибольшая частота вращения,
– наибольшая частота вращения,
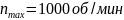 ;
;
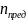 – предельная
частота вращения.
– предельная
частота вращения.
В
качестве предельной частоты вращения
принимают наименьшую из
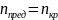 и
и
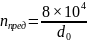 ,
где
,
где
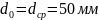 – средний диаметр винта.
– средний диаметр винта.
 .
.
Критическая
частота вращения
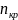 определяется по формуле:
определяется по формуле:
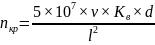 , (2.31)
, (2.31)
где
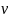 – коэффициент, зависящий от способа
закрепления винта, для случая, когда
оба конца заделаны жестко
– коэффициент, зависящий от способа
закрепления винта, для случая, когда
оба конца заделаны жестко
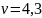 ;
;
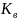 – коэффициент
запаса по частоте вращения,
– коэффициент
запаса по частоте вращения,
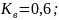
–внутренний
диаметр винта,
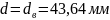 ;
;
– длина неопорного участка винта.
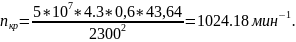
Динамическая
устойчивость обеспечивается, т.к. 1000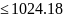 т.е. соблюдается условие устойчивости
(2.30).
т.е. соблюдается условие устойчивости
(2.30).
