Практическая работа №4
ПОСТРОЕНИЕ ИНКЛИНОГРАММЫ ПО ДАННЫМ ИЗМЕРЕНИЙ ИСКРИВЛЕНИЯ СКВАЖИН
Искривление скважины определяют для контроля за сохранением заданного направления скважины в пространстве и получения данных, необходимых при геологических построениях.
К вертикальным относят скважины, угол отклонения которых от вертикальной оси не превышает 1°. При отклонении на этот угол в одном направлении удаление забоя от вертикальной оси составит 0, 018*Н ( Н - глубина скважины, м ). Например, на глубине 2000 м удаление забоя будет равняться 36 м, что на чертеже масштаба 1:10000 составит всего 3,6 мм. Естественно, что таким углом отклонения можно пренебречь. Однако большие углы отклонения приводят к существенному удлинению ствола скважины и значительному удалению забоя от проекции устья скважины. Для учета влияния искривления скважины в последней необходимо определять угол отклонения от вертикали δ и азимут искривления φ. Под азимутом искривления понимается угол, лежащий в горизонтальной плоскости между направлением на магнитный север и горизонтальной проекцией элемента оси скважины.
Угол отклонения δ и азимут искривления φ замеряются в скважине специальным прибором, называемым инклинометром, спускается в скважину на трехжильном каротажном кабеле.
Данные замеров элементов искривления скважин помещают в таблицу ( табл., 1, колонки 1,2,3 ).
При обработке результатов замеров искривления скважин расстояние между двумя соседними точками ℓi=hi-1-hi принимают прямолинейным. Вычисляют вертикальную ∆Hi и горизонтальную ∆ℓi проекции расстояния ℓi между соседними точками. Согласно рис. 1, вертикальные и горизонтальные проекции будуг соответственно равны:
∆Hi = ℓi · cosδi; ∆ℓi = ℓi · sinδi. (1)
Экспериментальным путем установлено, что наименьшая погрешность при определении суммарных поправок на искривление скважины достигается в том случае, если в формуле (1) длина элементарного отрезка умножается на синус и косинус среднего угла между соседними точками замеров, т.е.
∆Hi = ℓi ∙ cos(0,5 ∙ (δi + δi+1)); (2)
∆ℓi = ℓi ∙ sin(δi + δi+1)); (3)
Значения ℓi, δср = (δi + δi+1)/2, а также вычисленные по
формулам (2) и (3) значения ∆Hi и ∆ℓi заносим в соответствующие графы табл. 1 (4, 5, 6, 7).
Глубина замера hi, м |
Угол искривл. δi |
Азимут искривления φi |
ℓi=hi+1- hi |
δср=(δi+δi+1)/2 |
∆Hi |
∆ℓi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Таблица 1
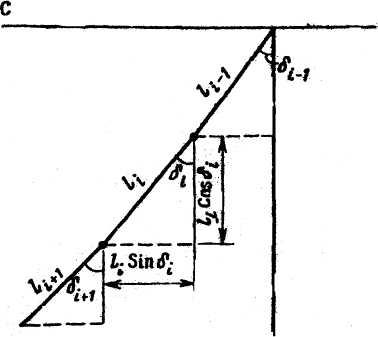
Рис. 1. Проекция участка ствола скважины на вертикальную плоскость
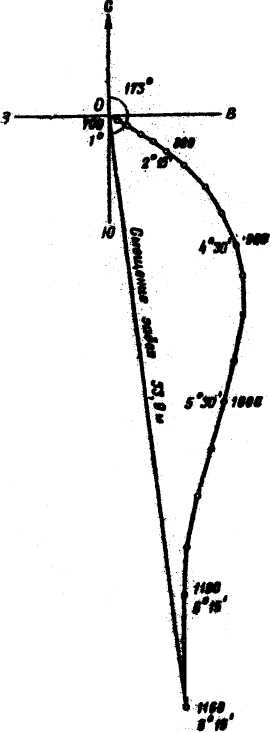
Рис. 2. Горизонтальная проекция ствола скважины. Забой скважины 1160 м; смещение забоя 33,9 м; азимут смещения 173°; удлинение скважины 1,7 м.
Для учета искривления скважины в плане строится специальный чертеж, называемый инклинограммой. На листе миллиметровки через точку О проводят оси координат С-Ю, З-В. За начало координат принимается точка, ниже которой инклинометром зафиксировано отклонение скважины от вертикальной оси (при построении инклинограммы замеры учитываются сверху вниз). Эта точка должна совпадать с горизонтальной проекцией устья скважины.
Затем отмечают точку с координатами (X0, Y0), с которой начнется построение участка инклинограммы. Из этой точки проводят прямую в направлении азимута искривления φ1 первого интервала, отклоненного от вертикальной оси. На этой прямой в масштабе чертежа (1:200, иногда в масштабе 1:100) откладывается отрезок, равный горизонтальной проекции ∆ℓ1 первого искривленного интервала. К концу отрезка первого интервала пристраивают проекцию второго интервала ∆ℓ2 в направлении его азимута φ2. Таким же образом строят горизонтальные проекции всех элементарных интервалов до забоя скважины.
Пример построения инклинограммы приведен на рис.2. Проекции отдельных интервалов необходимо строить как можно точнее, так как все допущенные при построениях ошибки суммируются.
После этого начало координат соединяют прямой линией с концом проекции последнего интервала. По длине отрезка прямой (с учетом масштаба чертежа) между указанными точками находят смещение забоя скважины от вертикали, а по направлению - азимут φ этого смещения.
Наконец, определяют абсолютную отметку забоя, суммируя все значения в колонке 6 табл. 1:
Hабс = ∑∆Hi + Z0 (4)
Здесь Z0 - бесконечная отметка точки, с которой начинается построение инклинограммы.
Используя соотношение (4), определим истинную глубину скважины - ее вертикальную проекцию:
H = Hабс + (±А) = Σ∆Hi + Z0 + (±А). (5)
Величина А - отметка роторного стола, от которого ведётся отсчет глубин. Отметка стола ротора, иначе называемая альтитудой устья скважины, определяется геодезической привязкой от ближайшего высотного репера на поверхности. Если роторный стол расположен выше уровня моря, альтитуда имеет знак плюс, если ниже, то минус.
Разница между наклонной дл иной L и ее вертикальной проекцией H называется поправкой на искривление скважины, или просто удлинением скважины:
∆L = L - H , ( 6 )
где L - длина ствола скважины (максимальная глубина замера в колонке 1 табл.1).
Для вычисления абсолютной отметки, например, кровли пласта Hабс, вскрытого искривленной скважиной, необходимо от глубины залегания кровли этого пласта Lпл, фиксируемой на каротажной диаграмме, вычесть альтитуду устья со своим знаком ± А и удлинение скважины до этой глубины:
Hабс = Lпл - (± А) - ∆L (7)
Вычисленными таким образом абсолютными отметками пользуются при всех структурных построениях.