2.1.3. Определение начальных диаметров зубчатых колес и межосевых расстояний.

Начальные диаметры d_w зубчатых колес определяются по формуле

d_w = Z  m

Расчетные значения диаметров в табл. 2.1.

Таблица 2.1. Начальные диаметры зубчатых колес

Z	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9	Z10	Z11	Z12
dw	132	168	117	183	69	231	60	240	241,5	122,5	87,5	276,5

Межосевые расстояния a_w зубчатых колес определяются по формуле

Расчетные значения межосевых расстояний заносим в табл. 2.2.

Таблица 2.2. Значения межосевых расстояний

aW (I - II)	aW (II - III)
150 мм	182 мм

2.1.3 Расчет клиноременной передачи

Исходя из величины передаваемого крутящего момента, выбираем клиновой ремень сечения «Б», площадь сечения =138 .

Расчетный диаметр ведущего шкива определяем по вормуле:

мм

Согласно ГОСТ 20889-88 принимаем диаметр ведущего шкива мм

Диаметр ведомого шкива:

,

где

мм

Согласно ГОСТ 20889-88 принимаем диаметр ведомого шкива =236 мм

Фактическое значение передаточного отношения:

Расчетная длина ремня:

,

где мм,

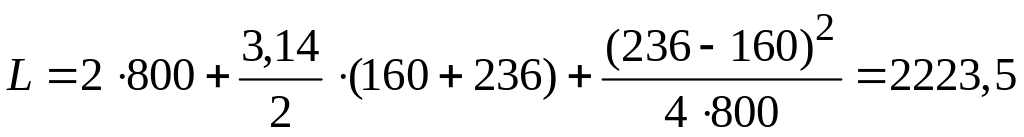Принимаем =800 мм :

мм

Выбираем ближайшую стандартную длину ремня =2240 мм

Уточненное межцентровое расстояние:

,

где мм ,

мм,

мм,

Скорость ремня:

,

Число пробегов ремня в секунду:

,

Окружное усилие:

Н,

Величина угла обхвата меньшего (ведущего) шкива:

,

Величина допускаемого полезного напряжения:

,

где -приведенное полезное напряжение, =1,8 МПа;

- коэффициент, учитывающий влияние угла обхвата на меньшем шкиве на тяговую способность ремня, =1;

- коэффициент, учитывающий влияние центробежных сил, =1,03;

-коэффициент, учитывающий условия работы передачи, =0,9;

МПа,

Количество ремней

2.2. Проверочные расчеты типовых деталей привода.

Проверочные расчеты проводятся с целью уточнения геометрических размеров валов зубчатых колес, подшипников, шпинделя и т.д. полученных на основе проектного расчета.

Как известно, проектный расчет не учитывает возможности собственных или контактных деформаций валов, подшипников, шпоночных и шлицевых соединений, что в ряде случаев приводит к потере точности и производительности станка.

Поэтому необходимо выполнить:

• проверочный расчет валов на прочность и жесткость,

• расчет зубчатых колес на выносливость по контактным напряжениям и напряжениям изгиба,

• выбор подшипников по их динамической грузоподъемности и точности,

• расчет шпинделя на жесткость с учетом податливости опор.

2.2.1. Проверочные расчеты валов на прочность.

Расчет валов на прочность сводится к определению коэффициентов запаса статической и усталостной прочности от изгибающих и касательных напряжений.

Определение запасов статической прочности валов.

Вал I.

Исходные данные:

Крутящий момент на первом валу T_I = 86,7 Нм;

Диаметр шестерни находящейся в зацеплении =60 мм;

Угол зацепления ;

Угол между направлением действия силы и вертикальной осью y,

Усилие действующее от клиноременной передачи:

Н.

Усилие в зацеплении :

Окружное усилие зубчатого колеса

Радиальное

Усилия действующие в вертикальной плоскости:

Усилия действующие в горизонтальной плоскости:

Уравнения равновесия I вала в вертикальной плоскости имеют вид:

Изгибающие моменты в вертикальной плоскости:

Уравнения равновесия I вала в горизонтальной плоскости имеют вид:

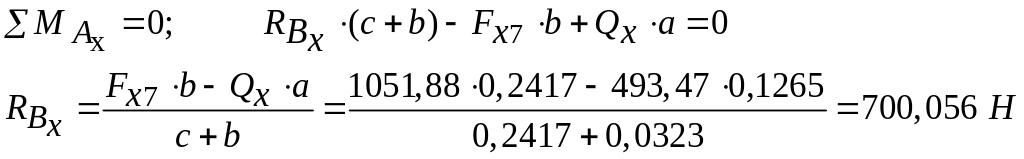
Изгибающие моменты в горизонтальной плоскости:

Суммарный изгибающий момент в наиболее нагруженном сечении:

Амплитудное значение напряжения в опасном сечении

а) нормальное:

где W-момент сопротивления сечения изгибу, мм³

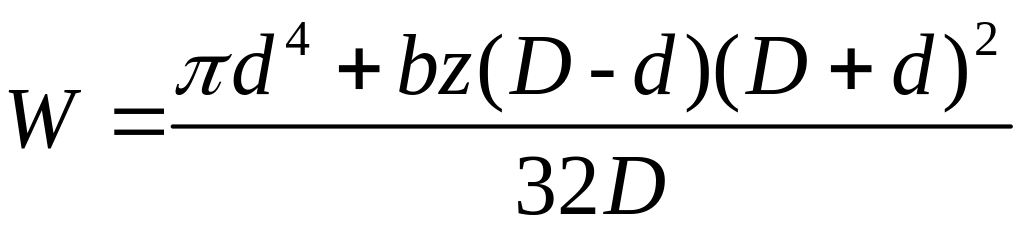
б) касательное:

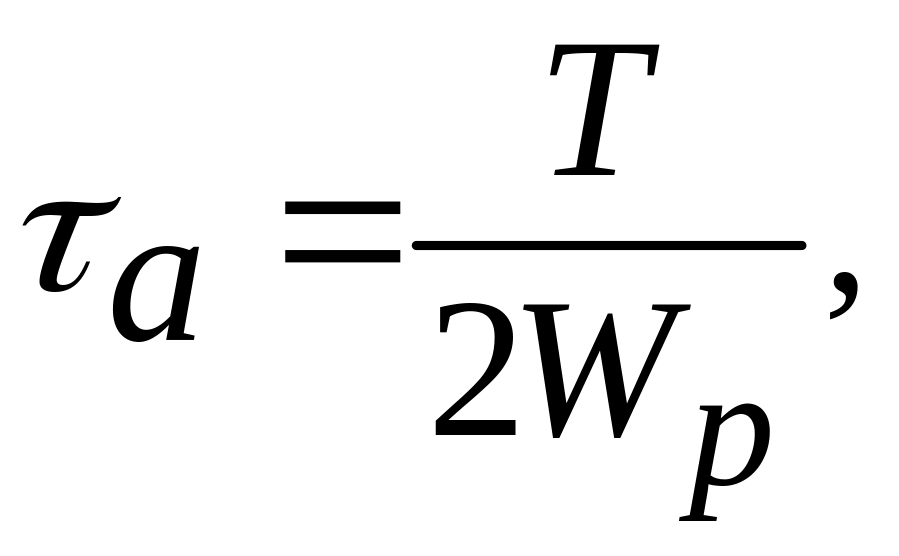
где W_P – полярный момент сопротивления кручению, мм³;

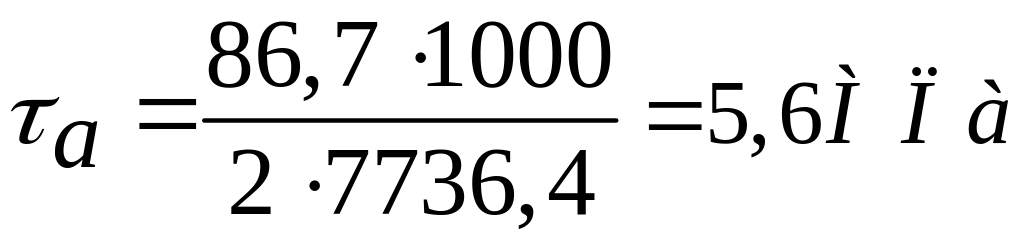
Эпюры изгибающих моментов I вала в вертикальной плоскости

Эпюры изгибающих моментов I вала в горизонтальной плоскости

Определение приведенных амплитудных напряжений с учетом коэффициента долговечности

,

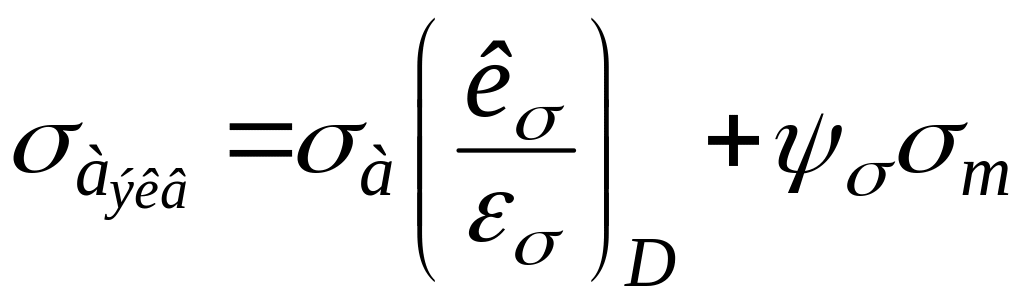где - коэффициент концентрации напряжений при изгибе; для вала со шлицами при МПа

- коэффициент учитывающий влияние абсолютных размеров вала на предел выносливости при отсутствии концентрации напряжений, для d=32 мм =0,87;

- коэффициент чувствительности материала вала к асимметрии цикла при изгибе;

;

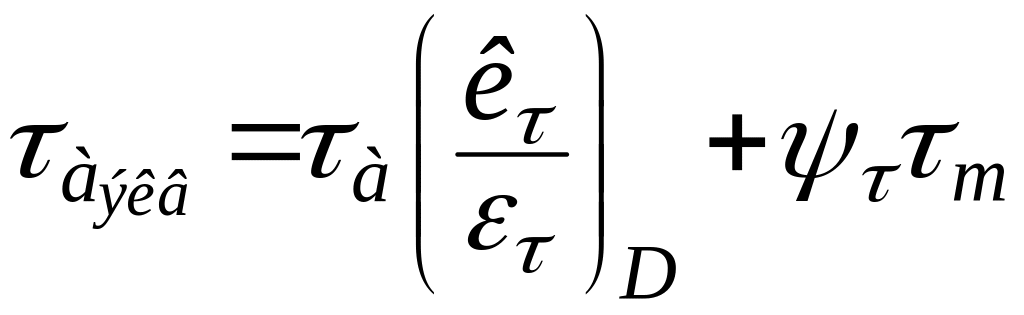где - коэффициент концентрации напряжений при кручении, для вала со шлицами при МПа

- коэффициент учитывающий влияние абсолютных размеров вала на предел выносливости при отсутствии концентрации напряжений, для d=32 мм ;

- коэффициент чувствительности материала вала к асимметрии цикла при кручении;

среднее касательное напряжение,

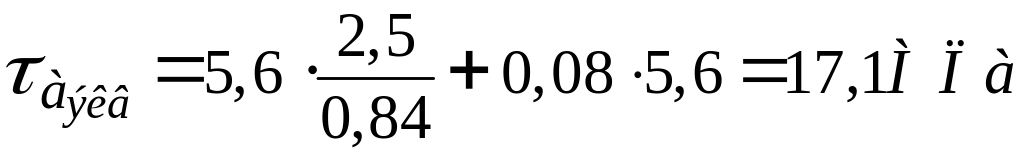
Запас прочности по нормальному напряжению

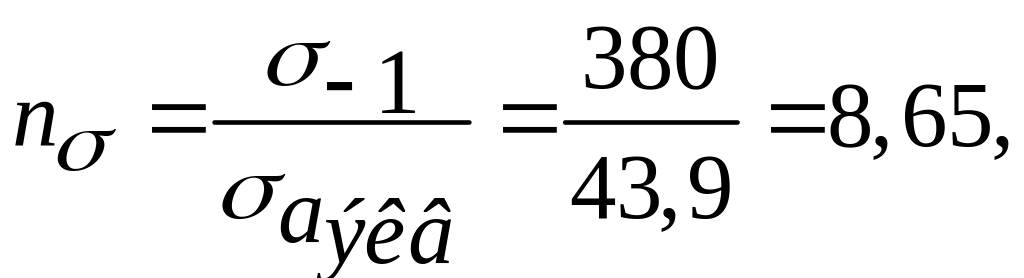
где предел выносливости,

Запас прочности по касательному напряжению

где предел выносливости по касательным напряжениям,

Фактический запас прочности по выносливости

Принимаем d₁=32 мм .

Вал II.

Исходные данные:

Крутящий момент на втором валу T_II = 354 Нм;

Диаметры зубчатых колес находящихся в зацеплении: =240мм, =87,5мм;

Угол зацепления ;

Угол между направлением действия силы и вертикальной осью y,

Угол между направлением действия силы и вертикальной осью y,

Усилие в зацеплении :

Окружное усилие зубчатого колеса

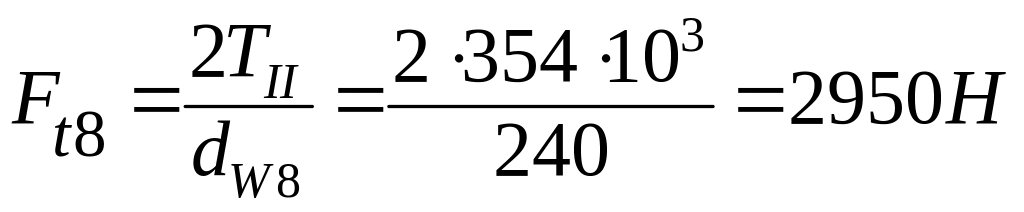
Радиальное

Усилие в зацеплении :

Окружное усилие зубчатого колеса

Радиальное

Усилия действующие в вертикальной плоскости:

Усилия действующие в горизонтальной плоскости:

Уравнения равновесия II вала в вертикальной плоскости имеют вид:

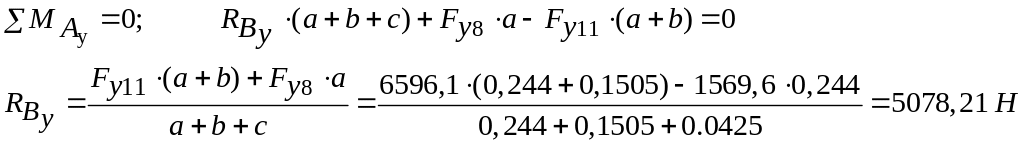
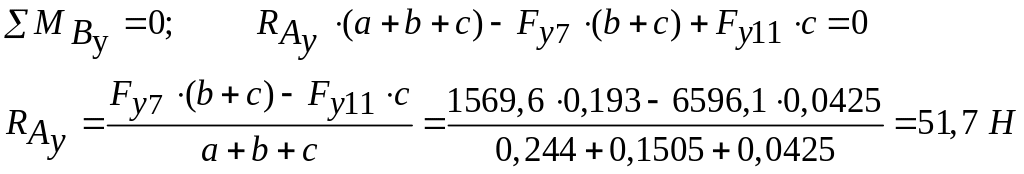
Изгибающие моменты в вертикальной плоскости:

Уравнения равновесия II вала в горизонтальной плоскости имеют вид:

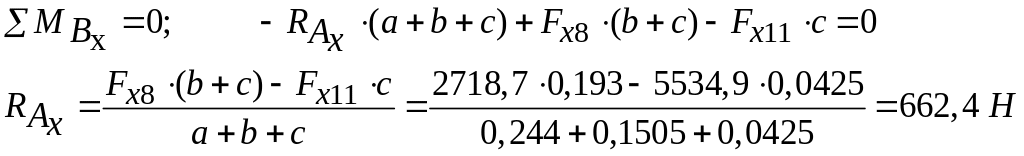
Изгибающие моменты в горизонтальной плоскости:

Суммарный изгибающий момент в наиболее нагруженном сечении:

Эпюры изгибающих моментов II вала в вертикальной плоскости

Эпюры изгибающих моментов II вала в горизонтальной плоскости

Амплитудное значение напряжения в опасном сечении

а) нормальное:

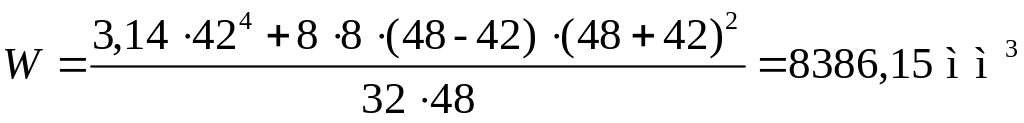
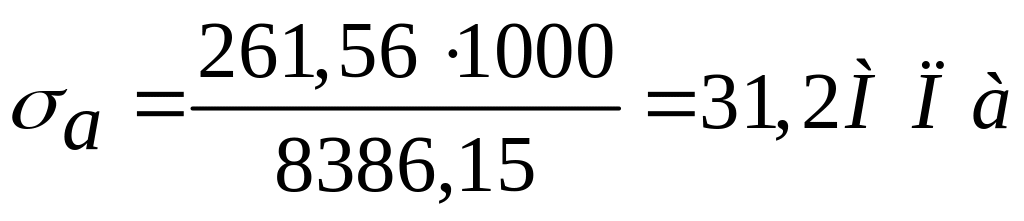
б) касательное:

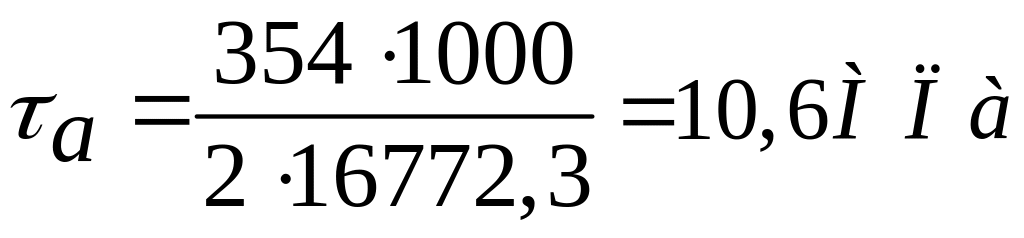
Определение приведенных амплитудных напряжений с учетом коэффициента долговечности

,

для вала со шлицами при МПа, ;

для d=42 мм, =0,85;

;

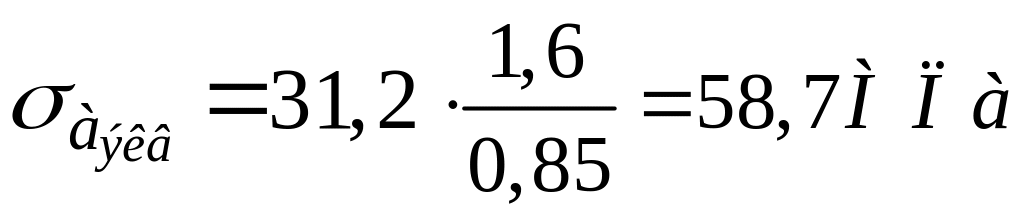
для вала со шлицами при МПа , ;

для d=42 мм, ; ;

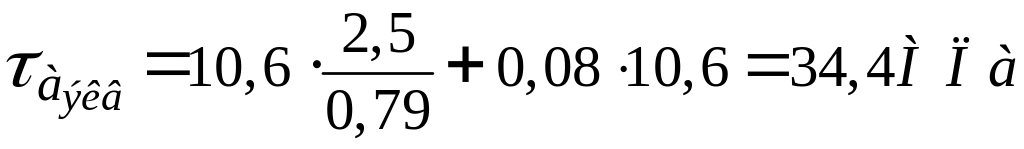
Запас прочности по нормальному напряжению

Запас прочности по касательному напряжению

Фактический запас прочности по выносливости

Принимаем d_II =42 мм.