1.3.2 Классы точности средств измерений

При измерениях в повседневной жизни повышенная точность не всегда нужна. Однако определенная информация о возможной инструментальной составляющей погрешности измерения необходима и поэтому она должна быть каким-либо образом отражена. Такая информация содержится в указании класса точности средства измерения.

Класс точности - обобщенная характеристика средства измерения, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значения которых устанавливают в соответствующих стандартах. Можно отметить такое примечание: «Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполненных с помощью этих средств».

Классы точности присваивают средствам измерений при разработке на основании исследований и испытаний представительной партии таких устройств. Обычно их устанавливают в технических условиях на средство измерения. Пределы допускаемых погрешностей нормируют и выражают в форме абсолютной (∆_си = ∆), относительной (δси ⁼ δ) или приведенной (γ_си = γ) погрешностей (далее индекс «си» для упрощения опущен). Форма выражения зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средства измерения.

Абсолютная погрешность средств измерений ∆_СИ = ∆ состоит из аддитивной (суммируемой с измеряемой величиной) и мультипликативной (умножаемой на измеряемую величину) составляющих. Аддитивная составляющая образуется, например, из-за неточности установки на нуль перед измерением и т.д. Мультипликативные погрешности появляются вследствие изменения коэффициента усиления усилителя, коэффициента передачи цепи.

1.3.3 Общие сведения об обработке результатов измерений

Из-за влияния многочисленных и принципиально неустранимых факторов, обусловливающих случайные погрешности, результат каждого измерения A_i будет отличаться от истинного значения X измеряемой величины: А_i - X = ΔX_i. Эту разность называют случайной погрешностью отдельного измерения.

Истинное значение X нам неизвестно. Однако, проведя большое количество измерений исследуемой величины X, можно выявить следующие статистические закономерности:

1) Если проводить серию измерений исследуемой величины и определить среднее значение, то положительные и отрицательные отклонения отдельных результатов измерений от среднего значения имеют приблизительно равную вероятность. Это является причиной того, что имеется равная вероятность (частота) отклонения результатов измерений от истинного значения величины в сторону уменьшения и увеличения, в том случае, когда систематическая погрешность равна нулю.

Среднее арифметическое значение, вычисленное на основании ряда измерений, является наиболее достоверным значением, которое можно приписать измеряемой величине. При вычислении среднего арифметического большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются.

2) Вероятность (частота) появления больших отклонений от полученного результата значительно меньше вероятности (частоты) появления малых отклонений. Эти статистические закономерности справедливы лишь при многократном повторении измерений.

После обработки результатов измерений, получается не абсолютно достоверный, а наиболее вероятный результат и этим результатом будет среднее арифметическое значение ряда измерений:

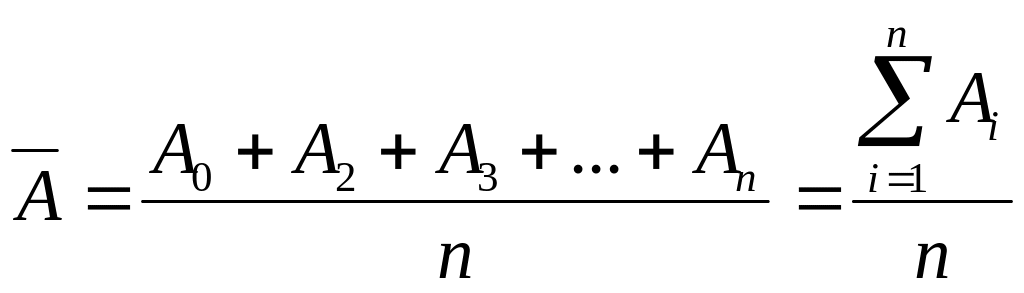, (1.11)

где n - число измерений.

Указанные статистические закономерности большого числа измерений позволяют поставить вопрос о законе, по которому происходит распределение случайных погрешностей. В практике электрорадиоизмерений наиболее распространенным законом распределения погрешностей является гауссовский закон распределения. Аналитически он описывается выражением:

(1.12)

где р(ΔХ) - плотность вероятности случайной погрешности ΔХ = А-X; σ - параметр, характеризующий степень случайного разброса результатов отдельных измерений относительного истинного значения X.

По своему смыслу плотность вероятности равна отношению вероятности попадания случайной величины внутрь интервала ΔХ к длине этого интервала в предположении, что последняя стремится к нулю.

Величину σ называют средним кнадратическим отклонением случайной погрешности измерения и определяют из соотношения:

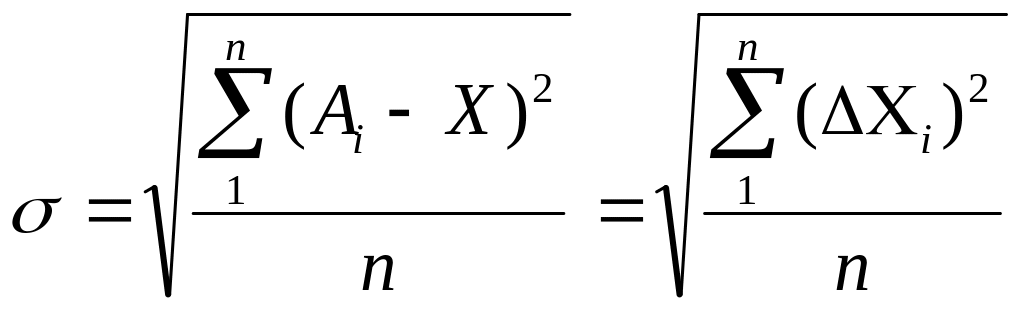, (1.13)

где А_i- численный результат отдельного измерения, n - число измерений.

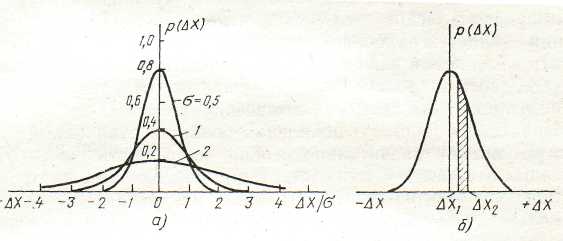Характер кривых, описываемых (1.13), показан на рис. 1.4, а для трех значений σ. Функция (1.4) графически изображается колоколообразной кривой, симметричной относительно ординат, асимптотически

Рисунок 1.4

приближающейся к оси абсцисс. Максимум этой кривой получается в точке ΔХ = 0, а величина этого максимума р (ΔХ)_max = l/σ . Как видно из рис. 1.4, чем меньше σ, тем уже кривая и, следовательно, тем реже встречаются большие отклонения, т. е. тем точнее выполняются измерения.

Как отмечалось ранее, среднее арифметическое ряда измерений является лишь наиболее достоверным значением измеряемой величины. Представляет интерес определение погрешности вычисления среднего арифметического значения. Оценивается эта погрешность с помощью величин, аналогичных тем, при посредстве которых производится оценка погрешности отдельного измерения. Если выполнить k серий измерений, в каждом из которых производится п отдельных измерений, и вычислить среднее арифметическое значение для каждой серии, то полученные средние арифметические значения _{1, 2, 3,} …, _n будут несколько различаться между собой. Эти средние значения будут отличаться от истинного значения X измеряемой величины на случайные величины и, следовательно, будут распределяться около X по Гауссовскому закону (1.4). Для получения представления о случайном разбросе среднего арифметического относительно точного значения X измеряемой величины нужно вычислить среднее квадратическое отклонение от среднего арифметического. В теории погрешностей доказывается, что это отклонение в раз меньше средней квадратической погрешности отдельного измерения, т. е.

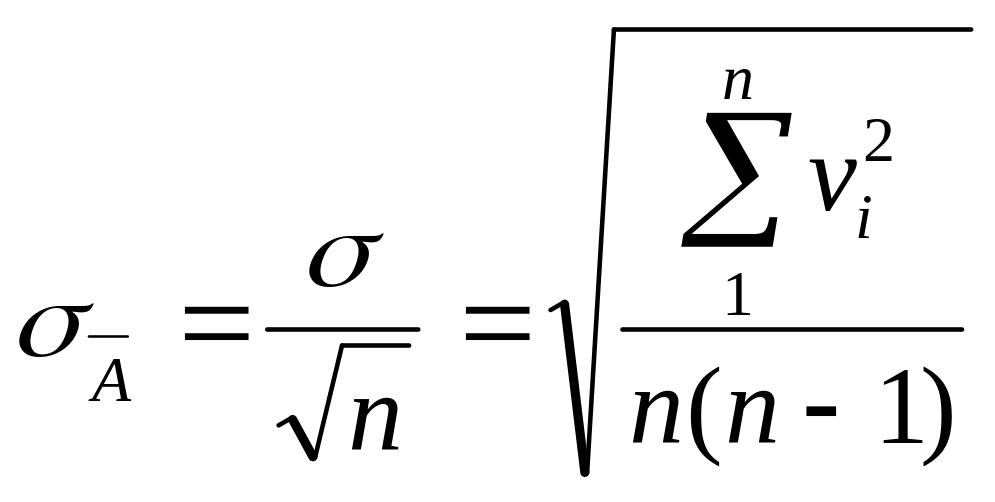, (1.14)

где - средняя квадратическая погрешность среднего арифметического из ряда измерений; σ - средняя квадратическая погрешность отдельного измерения; n - число измерений в серии. Из данного выражения видно, что увеличение числа повторных измерений n приводит к уменьшению средней квадратической погрешности результата измерений.

На практике (особенно при малом значении n) необходимо оценить точность и надежность полученных результатов для среднего значения и среднего квадратического отклонения. Для этой цели пользуются доверительной вероятностью и доверительным интервалом. Под доверительной вероятностью понимают вероятность появления погрешности, не выходящей за некоторые принятые границы. Этот интервал называют доверительным интервалом, а характеризующую его вероятность - доверительной вероятностью.

На практике приходится оценивать погрешности по результатам сравнительно небольшого количества измерения. Применение формулы (1.14) в этом случае дает заниженное значение доверительного интервала, т. е. оценка точности измерения оказывается неоправданно завышенной. В этом случае уточнить доверительный интервал можно с помощью коэффициентов Стьюдента t_n, которые зависят от задаваемой доверительной вероятности р и числа измерений n.

Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат можно записать так:

, (1.15)

Значения коэффициентов t_n, необходимых при расчетах приведены в табл. 1.1.

Общие сведения об обработке результатов измерений

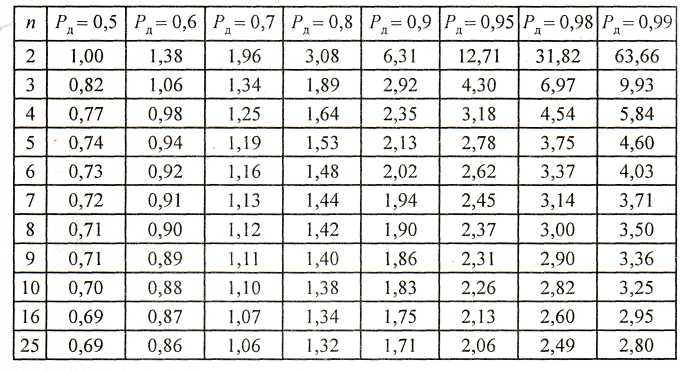Таблица 1.1 Коэффициенты Стьюдента t (P_д, n)