5 Выводы

Стандартный SPH-метод не точно описывает градиент давления в месте большого градиента плотности, поэтому в таких случаях не способен описать НКГ. Это происходит вследствие неточного расчета силы, действующей поперек градиенту плотности. Поперек градиенту плотности действует нефизическая сила, которая отталкивает частицы от начального разрыва, что создает щель и гасит начальное возмущение. Таким образом, развитие любой неустойчивости на градиенте плотности подавляется.

Неточный расчет силы происходит вследствие несогласованности стандартного SPH-метода. При аппроксимации частиц, используемой при выводе уравнения движения в стандартном SPH-методе, теряется согласованность нулевого порядка, если частицы распределены неравномерно. Для вывода уравнения импульса можно воспользоваться функцией Лагранжа, но в стандартном SPH-методе функция Лагранжа уже использует аппроксимацию частиц, поэтому в итоговом уравнении импульса по-прежнему будет присутствовать нефизическая сила, действующая поперек градиенту плотности.

Для того чтобы решить проблему согласованности стандартного SPH-метода, мы использовали новую формулировку I02, именуемую GSPH. Новое уравнение импульса было получено с помощью свертки ядра. Мы доказали, что уравнение импульса в методе GSPH имеет линейную согласованность до точности, при которой можно вычислить интеграл свертки ядра, что приводит к существенному снижению действия нефизической силы поперек градиенту плотности при равновесном давлении. То же уравнение импульса можно получить, используя новую функцию Лагранжа (I02). Оно очень похоже на функцию Лагранжа, используемую в стандартном SPH-методе, но оно более близко к функции Лагранжа для реальной жидкости.

Мы объяснили геометрическое значение уравнения движения в методе GSPH. Оно рассматривает основные и соседние частицы как растянутое тело и использует подробную информацию о растянутых тел. В стандартном SPH-методе основные частицы сглаживаются за счет вклада соседей, но эти соседи считаются точкой.

Для демонстрации работы GSPH были проведены расчеты тестовых задач двух типов. Один тест – это традиционный тест НКГ в двух слоях,

Рисунок 6. НКГ, развивающаяся в диагональном направлении. Это, по существу, тот же тест, что приведен на рисунке 3, но начальное распределение частиц повернуто на 45°. В отличие от сеточных методов Годунова, GSPH может описать многомерную задачу одномерным решением задачи Римана, поэтому не требуется декомпозиции оператора.

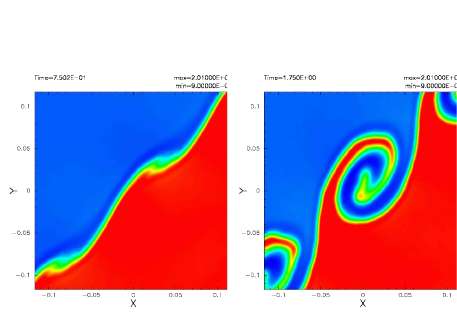
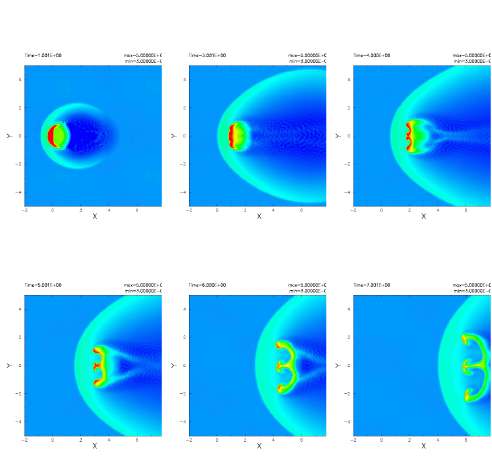
а другой – это тест с пузырем (каплей). В тесте с двумя слоями GSPH показал развитие НКГ даже при очень большом перепаде плотностей. Была проверена также НКГ, развивающаяся по диагонали, и получены удовлетворительные результаты. В тесте с пузырем по коду GSPH можно описать образование и развитие пальцевидных профилей на передней части сжатого пузыря вследствие неустойчивостей и комбинаций неустойчивостей. Результаты теста с пузырем по коду GSPH совпадают с результатами сеточных кодов.

В стандартном SPH-методе при неравномерном распределении частиц не согласуется не только уравнение импульса, но и уравнение сохранения энергии. Мы изучаем влияние несогласованности на уравнение сохранения энергии, и это тема нашей следующей работы.

Рисунок 7. Результаты теста с пузырем. Каждый снимок сделан при t = 1, 3, 4, 5, 6 и 7 τ_cc, начиная с верхнего левого угла, и показывает различные стадии развития пузыря внутри горячей движущейся окружающей среды. Мы взяли квадратный корень от столбцовой плотности для получения цветной карты плотности поверхности. На начальной стадии пузырь сжимается за счет лобового давления окружающей среды. В передней части сжатого пузыря можно увидеть головной скачок уплотнения. Окружающая среда, входя в головную ударную волну, замедляет движение, а затем инициируются неустойчивости Релея-Тейлора и Рихтмайера-Мешкова. Три пальцевидных профиля начинают образовываться в передней части пузыря (третий снимок), а затем эти пальцевидные профили усиливаются за счет неустойчивостей. На кончиках «пальцев» образуются грибовидные профили. Эти результаты хорошо совпадают с результатами сеточных кодов. Заметим, что это двумерное моделирование, в то время как тест пузыря в A07 был выполнен в трехмерном исполнении.

REFERENCES

Agertz O., Moore B., Stadel J., Potter D., Miniati F., Read J., Mayer L., Gawryszczak A., Kravtsov A., Nordlund Å., Pearce F., Quilis V., Rudd D., Springel V., Stone J., Tasker E., Teyssier R., Wadsley J., Walder R., 2007, MN-RAS, 380, 963

Balsara D. S., 1995, J. Comp. Phys., 121, 357

Barnes J., Hut P., 1986, Nature, 324, 446

Bryan G. L., Norman M. L., 1997, in Clarke D. A., West M. J., eds, Computational Astrophysics; 12th Kingston Meeting on Theoretical Astrophysics Vol. 123 of Astronomical Society of the Pacific Conference Series, Simulating X-Ray Clusters with Adaptive Mesh Refinement. pp 363-368

Cha S.-H., Whitworth A. P., 2003a, MNRAS, 340, 73

Cha S.-H., Whitworth A. P., 2003b, MNRAS, 340, 91

Courant R., Friedrichs K. O., 1948, Supersonic flow and shock waves. Interscience, New York

Despres B., 2003, Mathematics of Computation, 73, 1203

Dilts G. A., 1999, International Journal for Numerical Methods in Engineering, 44, 1115

Fryxell B., Olson K., Ricker P., Timmes F. X., Zingale M., Lamb D. Q., MacNeice P., Rosner R., Truran J. W., Tufo H., 2000, ApJS, 131, 273

Fulk D. A., 1994, PhD thesis, Air Force Institute of Technology

Gary J., 1966, SIAM J. Numer. Anal., 3, 467

Gingold R. A., Monaghan J. J., 1977, MNRAS, 181, 375

Inogamov N. A., 1999, Astrophysics and Space Physics Reviews, 10, 1

Inutsuka S.-I., 2002, J. Comp. Phys., 179, 238

Jones T. W., Ryu D., Tregillis I. L., 1996, ApJ, 473, 365

Klein R. I., McKee C. F., Corella P., 1994, ApJ, 420, 213

Kravtsov A. V., Klypin A. A., Khokhlov A. M., 1997, ApJS, 111, 73

LeVeque R. J., 2002, Finite Volume Mothods for Hyperbolic Problems. Cambridge University Press, Cambridge

Liu M. B., Liu G. R., 2006, Appl. Numer. Math., 56, 19

Liu M. B., Liu G. R., Lamb K. Y., 2003, J. Comp. Appl. Math., 155, 263

Lucy L. B., 1977, AJ, 82, 1013

Miniati F., Corella P., 2007, J. Comp. Phys., 227, 400

Monaghan J. J., 1982, SIAM J. Sci. and Stat. Comp., 3, 422

Monaghan J. J., 1987, SPH Meets the Shocks of Noh, Monash University Preprint

Monaghan J. J., 1989, J. Comp. Phys., 82, 1

Monaghan J. J., 1992, ARA&A, 30, 543

Monaghan J. J., 1997, J. Comp. Phys., 136, 298

Morris J. P., 1996, PASA, 13, 97

Murray S. D., White S. D. M., Blondin J. M., Lin D. N. C., 1993, ApJ, 407, 588

Price D. J., 2008, J. Comp. Phys., 227, 10040

Price D. J., Monaghan J. J., 2004, MNRAS, 348, 139

Ritchmyer R. D., Morton K. W., 1967, Difference Methods for Initial-Value Problems, 2^nd edn. No. 4 in Interscience Tracts in Pure and Applied Mathematics, John and Wiley & Sons, New York

Springel V., Yoshida N., White S. D. M., 2002, New Astronomy, 6, 79

Stone J. M., Norman M. L., 1992, ApJS, 80, 753

Swegle J. W., Hicks D. L., Attaway S. W., 1995, J. Comp. Phys., 116,123

van Leer B., 1997, J. Comp. Phys., 135, 229

Vietri M., Ferrara A., Miniati F., 1997, ApJ, 483, 262

Wadsley J. W., Stadel J., Quinn T., 2004, New Astronomy, 9, 137

Watkins S. J., Bhattal A. S., Francis N., Turner J. A., Whitworth A. P., 1996, A&AS, 119, 177

Yabe T., Hoshino H., Tsuchiya T., 1991, Phys. Rev. A, 44, 2756

1 НКГ можно инициировать и по схеме 1-го порядка, но она не очень хорошо развивается. Детали реализации GSPH 2-го порядка очень похожи на схему MUSCL (van Leer, 1997), и здесь не приводятся, поскольку описаны в I02