4 Тестирование

Было проведено два вида тестирования. Первый – это традиционное моделирование НКГ в двух слоях со сдвигом скоростей, а второй – тест с каплей. Все тесты проводились при помощи двухмерного кода GSPH второго порядка¹, в который заведено адиабатическое уравнение состояния. Отношение удельных теплоемкостей, γ, равно 5/3 во всех моделях.

4.1 НКГ в двух слоях (ρ_u : ρ_l = 1 : 2)

Имеется два слоя различной плотности при изначально равновесном давлении. Равновесное давление устанавливается равным 2.5, а отношение плотностей между верхним и нижним слоями полагается равным 1:2. Эти два слоя движутся в противоположных по отношению друг к другу направлениях с числами Маха в верхнем и нижнем слоях 0.22 и 0.3 соответственно. Расчетная область - [0, 1/3] x [- 1/6, 1/6]. Размера расчетной области меньше, чем у A07, с целью экономии времени вычисления. По осям х и y были заданы, соответственно, периодические и зеркальные граничные условия. Общее количество частиц внутри расчетной области составляет ~ 10⁵, а первоначальная конфигурация распределения частиц – решетка (A07).

Первоначальное возмущение скорости в направлении у определяется как

(24)

где A_o – амплитуда возмущения, которая устанавливается как 1/40 от первоначального сдвига скоростей. Здесь λ – это длина волны первоначального возмущения, которая устанавливается равной 1/6. Таким образом, в области вычисления ожидаются два вихря. Первоначальное возмущение задается только в тонком слое (|y| < 0.05) около первоначального контактного разрыва.

При таком первоначальном сдвиге скоростей и перепаде плотностей шкала времени для НКГ определяется выражением

(25)

Здесь ρ_u и ρ_l – плотности верхнего и нижнего слоев соответственно, а – разница скоростей между двумя слоями, τ_кг в условных единицах есть 0.43.

На рисунке 3 представлены снимки, сделанные в различные моменты развития, t = 0.5, 1.0, 1.5 и 2.0 τ_кг. При t = 0.5τ_кг начальный контактный разрыв колеблется вследствие первоначального возмущения и сдвига скоростей. В последующих снимках видны хорошо закрученные вихри, развивающиеся вокруг разрыва. На снимке, сделанном в момент времени t = 2.0τ_кг, видно искажение вихрей, и вокруг первоначального контактного разрыва ожидается образование смешанного слоя перемешивания. В конечном итоге слой перемешивания остановит развитие НКГ. В отличие от стандартного SPH-метода, GSPH намного меньше зависит от нефизической силы по градиенту плотности, поэтому с его помощью можно описать НКГ в слоях различной плотности. Заметим, что в данном моделировании нет никакой дополнительной явной диссипации, такой как искусственная вязкость (или искусственная теплопроводность).

На рисунке 4 показано распределение давления при t = 1.0 и 2.0 τ_кг, На нем видно, что помех значительно меньше, чем в расчетах по стандартному SPH-методу, в котором наблюдаются всплески давления поперек контактного разрыва (см. рис. 6 в Price (2008)). Заметим, что Price (2008) получил аналогичную карту распределения давления также и с использованием искусственной теплопроводности.

4.2 НКГ в двух слоях ((ρ_u : ρ_l = 1 : 10)

Моделирование НКГ, представленное в предыдущем разделе, было проведено еще, на сей раз с другим перепадом плотностей. Перепад плотностей намного больше того, который использовался в предыдущем моделировании, и составляет 1:10. Начальные числа Маха в верхнем и нижнем слоях равны 0.2 и 0.63 соответственно. Общее количество частиц, используемых в расчете, составляет ~ 10⁵. Первоначальное возмущение такое же, как и в предыдущем расчете.

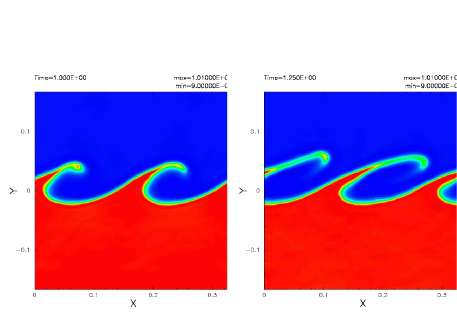
На рисунке 5 представлены результаты. Два снимка сделаны при t = 1.0 и 1.25 τ_кг соответственно. На более ранней стадии (до 1.0 τ_кг) ситуация очень сходна со случаем меньшего перепада плотностей, который рассматривался в предыдущем разделе. Однако на более поздней стадии завихрения не закручены, а растянуты.

Причина такого растяжения не понятна, но мы полагаем, что это может происходить вследствие худшего, по сравнению с предыдущим моделированием, разрешением верхнего слоя (Price 2008). GSPH (как и стандартный SPH-метод) является лагранжевым методом, поэтому численное разрешение зависит от численной плотности частиц. При аналогичном общем количестве частиц более высокий перепад плотностей между двумя слоями приводит в конечном итоге к худшему разрешению слоя с более низкой плотностью. Другой возможной причиной растяжения вихрей является начальное давление. В данном моделировании в качестве равновесного давления мы использовали значение 2.5, но если выбрать иное значение, то результат может измениться. Тем не менее, мы хотим особо отметить, что НКГ может иметь место в случае большой разницы плотностей.

4.3 НКГ в диагональном направлении

В отличие от сеточных методов Годунова, в GSPH все взаимодействия между частицами i и j ограничиваются до одномерной задачи на линии, соединяющей две взаимодействующие частицы, даже в трехмерных задачах. Таким образом, одномерное решение задачи Римана достаточно даже для многомерного кода SPH-Годунова.

В этом заключается преимущество GSPH по сравнению с сеточными методами Годунова, поскольку эффективного решения задачи Римана для случая многомерной задачи не существует. (Monaghan 1997). Метод декомпозиции оператора является ключевым в сеточных методах Годунова для описания многомерной задачи одномерной задачей Римана, но в GSPH никакой геометрической декомпозиции не требуется.

На рисунке 6 показано развитие НКГ в диагональном направлении. Перепад плотности составляет 1:2, и все начальные условия являются такими же, как в предыдущем моделировании, приведенном в разделе 4.1, за исключением начального распределения частиц. Начальное распределение частиц повернуто на 45°. Видны хорошо развитые вихри по диагонали рисунка.

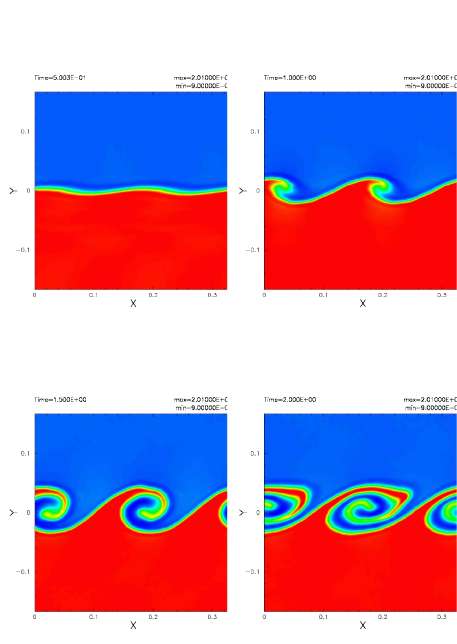
Рисунок 3. Моделирование НКГ в двух слоях различной плотности. Первоначальный перепад плотностей слоев составляет 1:2, а первоначальные числа Маха верхнего и нижнего слоев составляют 0.22 и 0.3 соответственно. Верхний слой движется вправо, а нижний слой движется влево. Первоначальный контактный разрыв между двумя слоями начинает извиваться вследствие первоначального возмущения, а затем вокруг разрыва развиваются хорошо закрученные вихри. Время каждого снимка нормализовано в единицах τ_кг и показано в верхнем левом углу каждого кадра.

Рисунок 4. Распределение давления в тесте, приведенном на рисунке 3, при t = 1.0 and 2.0 τ_кг – Данные карты распределения давления показывают, что помех значительно меньше, чем в стандартном SPH-методе, (см. рис. 6 в Price (2008)). Заметим, что Price (2008) получил аналогичные результаты с членом искусственной теплопроводности.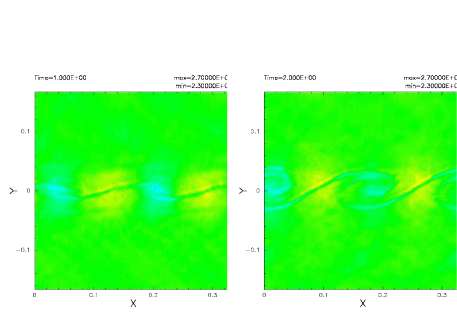

4.4 Тест с пузырем

Взаимодействие между плотным пузырем и сильной ударной волной – весьма интересный вопрос в контексте образования и развития звезд и галактик (Murray и др., 1993; Klein и др., 1994; Jones и др., 1996; Vietri и др., 1997). Если плотный пузырь столкнулся с ударной волной (например, звездный ветер или остаток вспышки сверхновой звезды), то он будет сжиматься и в конечном итоге разрушается. Разрушение плотного пузыря начинается за счет неустойчивостей Тейлора-Реле и Рихтмайера-Мешкова (Inogamov 1999), а затем усиливается за счет НКГ. Однако в стандартном SPH-методе неустойчивости или комбинация неустойчивостей практически не случаются по причине наличия нефизической силы впереди сжатого пузыря, поэтому пузырь в течение долгого времени сохраняется в сжатом состоянии в горячей окружающей среде (A07).

Мы провели тест с пузырем по коду GSPH. Расчетной областью теста с пузырем является [- 2, 30] x [- 6, 6]. Сначала плотный пузырь находится в начале координат и окружен горячей средой, движущейся в направлении х. Радиус пузыря равен 1, а отношение плотностей среды и пузыря χ определено равным 10. Начальное число Маха окружающей среды 5. Количество частиц, задействованных в пузыре и в окружающей среде, составляет 7688 и 93139 соответственно. Начальная конфигурация распределения частиц – стекло (A07). Скорость звука и плотность окружающей среды равны 1. При таких начальных условиях время разрушения облака (Klein и др., 1994), τ_cc определяется как

(26)

где r_b, и v_a – радиус пузыря и скорость окружающей среды соответственно. Jones и др., (1996) определили «время разрушения пули», но единственной разницей между τ_cc и временем разрушения пули является численный коэффициент (= 2), поэтому мы использовали τ_cc в качестве единицы времени в тесте с пузырем. В конечном итоге масштаб времени НКГ (A07) в тесте с пузырем определяется как

(27)

Рисунок 5. Моделирование НКГ со значительно более существенным перепадом плотностей. Нижний слой в 10 раз плотнее верхнего слоя. В области разрыва образуются вихри, которые затем вытягиваются и эволюционируют в течение долгого времени. Такое вытягивание может являться результатом низкого разрешения верхнего слоя.

τ_cc в данном тесте с пузырем составляет 0.63.

На рисунке 7 представлены результаты теста. На ранней стадии взаимодействия происходит сжатие. Передняя часть пузыря сжимается за счет лобового давления окружающей среды. Сзади пузырь испаряется. Вокруг сжатого пузыря образуется головная ударная волна, и в результате неустойчивостей Релея-Тейлора и Рихтмайера-Мешкова образуется три пальцевидных профиля. Эти пальцевидные профили усиливаются НКГ, что приводит к образованию грибовидного профиля на концах пальцевидных профилей. (например, Yabe и др., 1991). Результаты теста пузыря, выполненного по коду GSPH, аналогичны результатам, полученным при помощи сеточного кода (например, Klein и др., 1994).