2.9. Степень деформации и напряжённо-деформированные состояния (н.Д.С.) металла при вытяжке

Схема цилиндрической детали полученной из круглой заготовки показана на рисунке 2.24.

Рис. 2.24. Схема цилиндрической детали полученной из крупной заготовки:

1 – вытянутая деталь; 2 - исходная заготовка

Степень деформации: = 1- .

Коэффициент вытяжки: .

Чем меньше m, тем больше деформация при вытяжке.

Схема вытяжки с разбиением заготовки на зоны показана на рисунке 2.25.

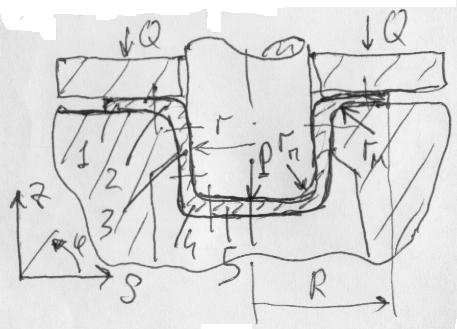
Рис. 2.25. Схема вытяжки с разбиением заготовки на зоны:

1 – фланец; 2 – поворот фланца на радиусе закругления матрицы ;

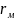3 - вертикальная стенка; 4 - поворот стенки на радиусе закругления пуансона 5 – дно; Q – усилие прижима; Р – усилие вытяжки

Схема н.д.с. на фланце.

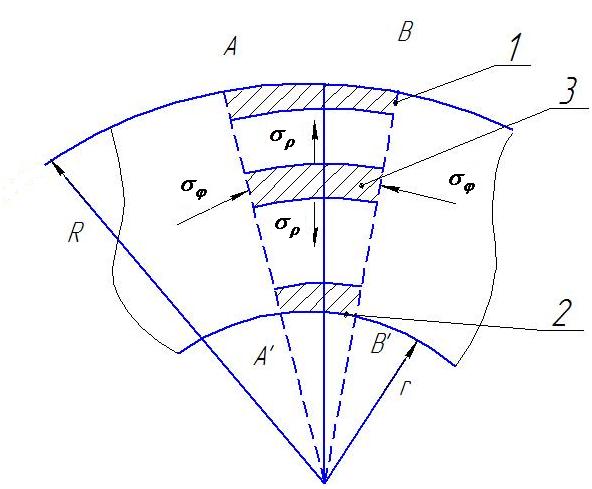
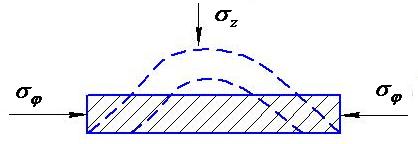
а) б)

Рис. 2.26. Схема деформирования фланца: а) вид сверху на малый элемент;

б) элемент заготовки на фланце под прижимом; 1 – положение малого элемента в начале деформации на фланце; 2 – конечное положение элемента; 3 – промежуточное положение элемента; АВ – длина элемента в начале деформации;

А’В’ – длина в конце

Сжимающие напряжения способствуют образованию складок. Напряжение (от действия прижима) не дают складкам образоваться.

Напряжения малы по сравнению с сопротивлением деформации (или напряжением текучести). Поэтому можно пренебречь.

При вытяжке диаметр фланца D = 2R уменьшается. Именно на фланце сосредоточен очаг пластической деформации. Условие пластичности:

.

Напряжения , поэтому приближенно можно принять, что схема н.с. плоская. Коэффициент .

Рис. 2.27. Схема н.д.с. на фланце

Схема н.д.с. на вертикальной стенке.

Вертикальный участок 3 в результате давления пуансона, передаваемого на данную часть заготовки, находится в условиях линейного растяжения. Растягивающее напряжение должно быть меньше Если это не будет выполнено, то произойдёт утонение стенки и отрыв дна. Вертикальные стенки деформируются упруго, т.е. деформации = 0.

Рис. 2.28. Схема напряжений на вертикальной стенке

Принято обозначать , хотя действует на стенке по вертикали. На фланце это напряжение было направлено по оси ρ. И именно оно перешло на вертикальную стенку.

Схема н.д.с. на донном участке.

Деформации равны нулю. Донный участок испытывает двухосное растяжение. Также как вертикальные стенки дно деформируется упруго: ; .

Рис. 2.29. Схема напряжений на донном участке

Кольцевой фланец вытягиваемой детали называется зоной пластической деформации, а вертикальную стенку и дно - зонами передачи усилий.

2.10. Оценка величины растягивающих напряжений на вертикальной стенке

С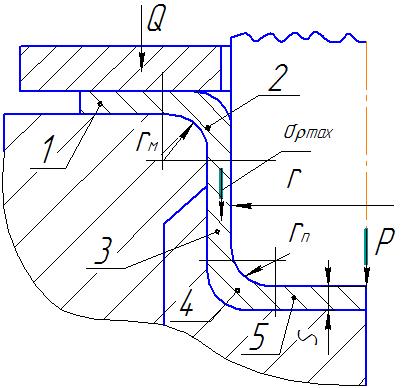 хема действия напряжения на вертикальной стенке показана на рис. 2.30.

Рис. 2.30. Схема действия напряжения на вертикальной стенке

– максимальное по очагу деформации радиальное растягивающее напряжение:

,

где напряжение пластической деформации на фланце (зона 1) в идеальных условиях (деформация металла без упрочнения, т.е. идеальная пластичность; трение отсутствует);

напряжение, вызванное трением между заготовкой, прижимом и матрицей на плоской её части (зона 1);

напряжение от изгиба заготовки при входе на закругленную кромку матрицы и спрямление при сходе с неё (зона 2);

напряжение, вызванное трением заготовки на кромке матрицы (зона 2).

Вывод формулы для производится в результате совместного решения дифференциального уравнения равновесия и условия пластичности, т.е. инженерным методом. Рассмотрим осесимметричную деформацию в цилиндрической системе координат ρ, z, ϕ.

Рис. 2.31. Цилиндрическая система координат

Дифференциальное уравнение равновесия:

.

Условие пластичности: .

В результате вывода можно получить формулу:

, внутренний радиус детали; радиус исходной заготовки ).

Напряжение трения , вызванное силой прижима Q, будет распределяться по узкой кольцевой части фланца. Эта часть граничит с наружным краем заготовки. Здесь толщина заготовки при деформации увеличивается. Ширина этой части примерно принята равной толщине металла s. Тогда можно получить формулу:

.

Здесь при выводе формулы силу трения разделили на площадь контакта.

Напряжение от изгиба заготовки на кромке матрицы и схода с неё определяется из равенства работ внешних сил. Силы и затрачиваются на изгиб материала и его спрямление. Работа внутренних сил определяется через момент пластического изгиба. Напряжения изгиба и распрямления элемента принимаются равными. Тогда можно получить формулу:

.

Влияние трения на закругленной кромке матрицы учитывает напряжение Это напряжение определяется с помощью цепного закона Эйлера о трении скольжения при натяжении ремня по шкиву.

Для учёта нужно сумму растягивающих напряжений умножить на величину (1 + 1,6μ). Здесь μ – коэффициент трения.

(1 + 1,6μ)

(1 + 1,6μ)

Для того, чтобы не было разрушения на вертикальной стенке необходимо выполнение условия , где предел прочности. Лучше даже . Тогда нет пластической деформации и утонения стенки;

.