Кафедра общественного здравоохранение и информатики

ИНФОРМАЦИОННО-ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

Предмет: Биостатистика

1 Сабақ Статистическая совокупность генеральная совокупность. Выборочная совокупность.

Статистическая совокупность представляют собой множествообъектов, однородных относительно некоторого качественного или качественного признака, характеризующего эти объекты.

Совокупность, состоящая из всех объектов, которые могут быть отнесены, называется генеральной совокупностью.

Число объектов генеральной совокупности называют её объёмом и назначают буквой «N».

Множество объектов, случайно отобранных из генеральной совокупности называется выборочной совокупностью или выборкой.

Число объектов выборочной совокупности называют её объёмом и обозначают буквой «n».

Ряд состоящей из количественного значения вариант с их частотой или относительной частотой называется статистическим дискретным рядом.

Изучаемый признак (х)

Частота признака (х) =m

∑ m= n Сумма «m» равно объёму выборки.

Отношение частоты (m) к объёму выборки (n) называют относительной частотой (P)

P= m/ n

Ряд содержащий частичные интервалы и их частоты или относительные частоты называют статистическим интервальным рядом распределения.

Относительная частота P= m/ n

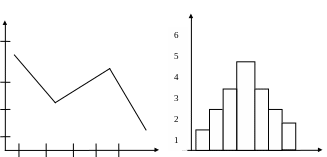
Полигон и гистограмма.

Для графического изображения статического распределения используются полигоны и гистограммы. Полигон обычно используются в случае небольшого количества вариант. В случае большого количества вариант и случае непрерывного распределения признака используют гистограмму.

По оси 0_х – откладывают значение вариант х, на оси 0_у –значение частот или относительных час10,10,1

1 2 3 4 5 5 10 15 20 25 30 40

П о л и г о н г и с т о г р а м м а

Характеристика генеральной совокупности с выборочным методом.

Вычисление средней выборочной:

=

m –частота, количественного признака

Х1	19	20	21	22	23
m1	2	1	6	8	2

= ∑m= n=19

Х = = = ; Х=21,3

Чтобы определить рассеянность значений количественного признака (х) генеральной совокупности вокруг своего среднего значения вводят характеристику генеральная дисперсия.

1. Генеральная дисперсия Д_r

Д_r =

2. Для характеристики количественного признака вокруг выборки, вокруг своего среднего значения выводят характеристику выборочная дисперсия Д_b

Д_b= Х_b=21,3

Д_b= = Д_b=0,55

Среднее квадратическое отклонение – которое характеризует разнообразие признака.

σ - среднее квадратическое отклонение

σ_r =√ Д_r (генеральные среднее квадратическое)

σ_b =√ Д_b (выборочние среднее квадратическое откланение.

Выборочные среднее квадратическое отклонение равно

σ_b =

Доверительный интервал ошибки статистического наблюдения.

Доверительная вероятность – вероятность с которой эта оценка покроет неизвестный параметр.

Доверительная вероятность – γ

Часто (γ) равно 0,9; 0,95; 0,99; 0,999

Продолжение задачи

γ ═

t –по таблице = 2,10

Доверительный интервал:

21,3- 0,36= 21,60

21,3+ 0,36= 20,94

З А Д А Ч И

1.Выборочная совокупность задана таблицей распределения

х1	1	2	3	4	5	6
m	10	20	15	10	12	5
р

Найти:

1. Выборочную среднюю

2. Выборочную дисперсию

3. Среднее квадратическое отклонение

4. относительную частоту

5. построить полигон

6. Стандартную ошибку

7. доверительный интервал

2.Рост мальчиков 8 лет

х1	115	116	117	118	119	120	121
m	1	2	6	10	15	20	30
р

Найти:

1. Выборочную среднюю

2. Выборочную дисперсию

3. Среднее квадратическое отклонение

4. относительную частоту

5. построить полигон

6. Стандартную ошибку

7. доверительный интервал

3.Вес новорождённых (кг)

х1 (см)	1,900	2,200	2,500	2,900	3,00	3,500	4,000	4,500
m	1	2	5	14	18	20	8	5
р

Найти:

1. Выборочную среднюю

2. Выборочную дисперсию

3. Среднее квадратическое отклонение

4. относительную частоту

5. построить полигон

6. Стандартную ошибку

7. доверительный интервал

Т Е С Т Ы

1. Генеральная и выборочная совокупности составляют:

1. Статистическую совокупность

2. Измерительную совокупность

3. Распределительную совокупность

4. Интервальную совокупность

5. Эмпирическую совокупность

2. Число объектов в совокупности называют:

1. Признак

2. Вариантой

3. Частотой

4. Объёмом

5. Дисперсией

3. Что можно определить указанной формулой?

1. Относительную частоту

2. Объём выборки

3. Среднюю выборку

4. Среднюю дисперсию

5. Квадратическое отклонение

4. При небольшом количестве вариант какое графическое изображение используют?

1. Секторную

2. Столбиковую

3. Полигон

4. Гистограмму

5. Внутристолбиковую

5. Дан дискретный вариационный ряд:

Х1	1	2	3	4
m	20	15	10	5

Чему равен объём выборки

1. 20

2. 25

3. 5

4. 10

5. 50

6. Если сумма произведенный варианты частоте равен 520, объём выборки n =27.

Чему равен среднее выборочное?

1. 2,3

2. 22,3

3. 19,2

4. 18,5

5. 21,3

7. Среднее выборочное дисперсия равно. σ = 0,57. Чему равен среднее квадратическое отклонение?

1. 0,61

2. 0,32

3. 0,33

4. 0,72

5. 0,12

8. Что характеризует генеральная дисперсия?

1. Разнообразие признака

2. Рассеянность признака

3. Частоту признака

4. Количество признака

5. Объём признака

9. Что можно определить с помощью данной формулы σ_b =√ Д_b ?

1. Среднеквадратическое отклонение

2. Генеральная дисперсия

3. Выборочная дисперсия

4. Выборочное среднее

5. Генеральное среднее

10. Вероятность с которой, эта оценка покроет неизвестный параметр называется?

1. Совокупностью

2. Средней величиной

3. Генеральной дисперсией

4. Частотой

5. Доверительной вероятностью