Глава 3. Динамические звенья и их характеристики

3.1. Виды элементарных динамических звеньев

Для любых систем, в которых протекают процессы управления (технические системы или живые организмы), характерна одна общая черта: отдельные элементы этих систем взаимосвязаны так, что передают друг другу некоторые сообщения о происходящих в них процессах посредством сигналов, т.е. информации. По этому признаку можно установить глубокое сходство и единство процессов управления.

Информация всегда связана с некоторым материальным носителем (физической величиной). В технических системах материальные носители информации называют носителями сигналов (например, электрическое напряжение и ток, давление, механическое перемещение и др.), которые можно изменять в соответствии с передаваемой информацией. Конструктивные элементы системы должны преобразовывать одни физические величины (и соответствующие им сигналы) в другие. Этот процесс отражается в кибернетическом понятии звена.

Звено – это входящий в систему автоматического управления элемент, в котором входной сигнал преобразуется в выходной по определенному закону или правилу. Схематически звенья изображаются в виде блоков, причем такое изображение не отражает особенностей их конструкции. Интерес представляет только связь между воздействием на вход звена и его реакцией на выходе. Такой подход позволяет создавать модели элементов различных технических или природных систем и имитировать их поведение, что значительно облегчает поиск эффективных методов управления.

Непременное условие, которое должно соблюдаться при членении системы на звенья, состоит в соблюдении правила однонаправленной передачи воздействий. Это означает, что выходная величина любого звена системы зависит от изменения его входной величины, однако обратное влияние выходной величины непосредственно через рассматриваемое звено на входную величину должно отсутствовать.

Среди всего разнообразия звеньев особого внимания заслуживают так называемые элементарные звенья, описываемые дифференциальными уравнениями первого и второго порядков, поскольку из таких звеньев чаще всего строятся математические модели систем управления.

Идеальное усилительное (безынерционное) звено. Уравнение данного звена имеет вид

, (3.1)

где - коэффициент усиления или передачи, а и - соответственно входной и выходной сигналы.

Определим передаточную функцию безынерционного звена. Для этого применим к уравнению (3.1) преобразование Лапласа

. (3.2)

Исходя из равенства (3.2) установим, что

. (3.3)

Получим выражения для переходных характеристик рассматриваемого звена. Подадим на его вход единичное ступенчатое воздействие , т.е. . Тогда уравнение (3.1) принимает вид

.

Дифференцируя переходную характеристику по времени согласно выражению (1.3.15) определим импульсную переходную характеристику звена

.

Выполнив в равенстве (3.3) замену получим выражение для КЧХ звена

. (3.4)

Исходя из выражений (2.56) – (2.58) и (3.4) определим АЧХ и ФЧХ данного звена

; .

Примерами безынерционных звеньев могут служить жесткие механические и гидравлические передачи, электронный усилитель сигналов на низких частотах, гироскоп и некоторые другие измерительные датчики.

Идеальное интегрирующее звено. Уравнение и передаточная функция звена имеют вид

; ,

где - коэффициент передачи.

Переходная и импульсная переходная характеристика определяются выражениями

; . (3.5)

Частотные характеристики рассматриваемого звена представимы в виде

; ; ..

Примером такого звена является двигатель с переменной частотой вращения вала, скорость перемещения поршня которого может считаться пропорциональной смещению штока золотника.

Идеальное дифференцирующее звено: Уравнение и передаточная функция звена имеют вид

; ,

где - коэффициент передачи.

Переходная и импульсная переходная характеристика задаются выражениями

; .

Частотные характеристики идеального дифференцирующего звена:

; ; . (3.6)

В реальных системах характеристики идеального дифференцирующего звена можно реализовать лишь с той или иной степенью приближения, т.к. порядок правой части его дифференциального уравнения больше чем левой. Поэтому, например, согласно (3.6) амплитуда выходного сигнала данного звена неограниченно увеличивается с ростом частоты, что требует бесконечной энергии.

Апериодическое (инерционное) звено: Уравнение и передаточная функция звена:

; , (3.7)

где - постоянная времени; - коэффициент передачи.

Получим формулу для переходной характеристики апериодического звена, воспользовавшись выражением (1.3.9), в котором полагаем .

В результате имеем

. (3.8)

График переходной функции апериодического звена представлен на рис. 3.1, где , а .

Рис. 3.1.

Обратим внимание, что в отличие от звеньев, описываемых дифференциальными уравнениями более высоких порядков, переходная характеристика апериодического звена, как видно из рис. 3.1, не имеет точки перегиба.

Продифференцировав по времени равенство (3.8) получим выражение для импульсной переходной функции звена

.

Вид импульсной переходной функции для апериодического звена показан на рис. 3.2, где , .

Рис. 3.2.

Частотные характеристики апериодического звена:

; ; .

Примерами апериодического звена являются электродвигатель (в первом приближении), если - управляющее напряжение, - угловая скорость вала, а также цепочка , в которой - входное напряжение, а - ток в цепи.

Инерционное интегрирующее звено. Уравнение и передаточная функция звена:

; ,

где - постоянная времени; - коэффициент передачи.

Переходные характеристики имеют вид

; . (3.9)

Сопоставив выражения (3.5) и (3.9) приходим к выводу, что за счет постоянной времени вместо идеального интегрирования получается интегрирование с инерционным запаздыванием.

Частотные характеристики звена:

; ;

.

Примером инерционного интегрирующего звена является электродвигатель, если выходной величиной считать угол поворота вала двигателя.

Инерционное дифференцирующее звено. Уравнение и передаточная функция звена:

; ,

где - постоянная времени; - коэффициент передачи.

Переходные характеристики данного звена имеют вид

; .

Частотные характеристики звена:

; ;

.

Здесь мы видим реальное ограничение амплитуды выходного сигнала звена при увеличении частоты.

Для того, чтобы свойства инерционного дифференцирующего звена приблизились к свойствам идеального, необходимо одновременно увеличивать коэффициент передачи и уменьшать постоянную времени так, чтобы их произведение оставалось постоянным . Отметим, что в размерность входит время.

Примерами такого типа звена являются обычная цепочка , трансформатор, механический демпфер с пружиной.

Интегродифференцирующее звено первого порядка: Уравнение и передаточная функция звена имеют вид

; (3.10)

,

где - коэффициент передачи; и - постоянные времени.

Переходная характеристика рассматриваемого звена описывается следующим выражением:

(3.11)

Как видно из выражения (3.11) переходная характеристика при возрастает со временем, а при - убывает. Соответствующие графики представлены на рис. 3.3.

Рис. 3.3. Переходные характеристики интегродифференцирующего звена:

1 - , , ; 2 - , , .

Если , то функция определяется выражением и при принимает постоянное значение равное , как показано на рис 3.4.

Рис. 3.4. Переходная характеристика интегродифференцирующего звена при .

Таким образом, переходные характеристики объектов, у которых входное воздействие подвергается дифференцированию по времени, претерпевают скачок при . Переходные характеристики объектов, у которых такое дифференцирование отсутствует, плавно возрастают со временем.

Дифференцируя выражение (3.11) по времени имеем

Частотные характеристики интегродифференцирующего звена:

; ;

.

Апериодическое звено второго порядка. Дифференциальное уравнение и передаточная функция звена:

; ,

причем предполагается, что

. (3.12)

При выполнении неравенства (3.12) квадратное уравнение

, (3.13)

называемое также характеристическим уравнением звена, имеет два вещественных отрицательных корня

. (3.14)

Передаточную функцию рассматриваемого звена, разложив ее знаменатель на сомножители, можно представить в виде

,

где

.

Переходные характеристики звена:

;

.

Частотные характеристики звена:

; ;

.

Примерами такого звена являются двигатель постоянного тока при учете инерционности цепи якоря, электромашинный усилитель, двойная цепочка .

Колебательное звено. Уравнение звена имеет вид

,

причем предполагается

,

так что корни характеристического уравнения (3.13) – комплексные.

Общепринята запись передаточной функции колебательного звена в виде

,

где , , причем , т.к. при звено становится апериодическим (второго порядка).

Переходные характеристики звена:

;

.

Предположим, что , и построим графики переходных характеристик и при различных значениях параметра .

На рис. 3.5 представлены переходные характеристики колебательного звена.

Рис. 3.5. Переходные характеристики колебательного звена:

1 – ; 2 – ; 3 – .

Согласно рис. 3.5 с уменьшением значений параметра возрастает амплитуда колебаний переходного процесса на выходе звена, а также уменьшается скорость затухания его колебаний.

На рис. 3.6 представлены импульсные переходные характеристики колебательного звена.

1

Рис. 3.6. Импульсные переходные характеристики колебательного звена:

1 – ; 2 – ; 3 – .

Из рис. 3.6 видно, что скорость затухания колебаний характеристики увеличивается с ростом значений параметра , но при этом также возрастают ее максимальные значения, что отличает эту характеристику от характеристики .

Частотные характеристики звена:

;

; (3.15)

.

В случае, если амплитуда уменьшается с увеличением , т.е. . При появляется «горб» на характеристике , который уходит в бесконечность при . Поэтому величина называется параметром затухания. Отсюда видна роль постоянных времени и в уравнении звена: постоянная «раскачивает» колебания, а - «демпфирует» их.

При колебания становятся незатухающими, а при колебания вырождаются в апериодический процесс. Частный случай колебательного звена при , когда функции и становятся незатухающими (периодическими), носит название консервативного звена.

Графики АЧХ колебательного звена приводятся на рис. 3.7.

Рис. 3.7. АЧХ колебательного звена: 1 – ; 2 – ; 3 – .

Колебательному характеру переходных характеристик и соответствует наличие в графике АЧХ резонансного пика при частоте резонанса . Отношение максимального (пикового) значения АЧХ к ее значению при нулевой частоте получило, поэтому название показателя колебательности:

. (3.16)

Продифференцировав выражение (3.15) по и приравняв производную к нулю, получим выражение для резонансной частоты системы

. (3.17)

Подстановка выражения (3.17) в формулы (3.15) и (3.16) приводит к следующей формуле для определения значения показателя колебательности:

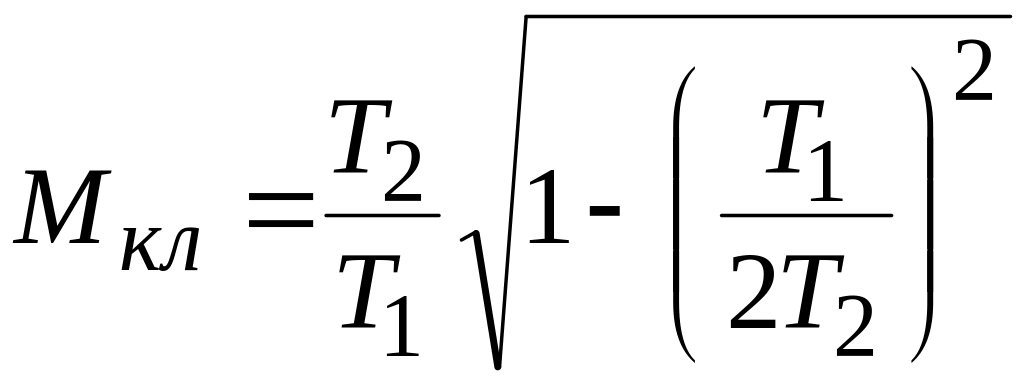. (3.18)

Об интенсивности затухания колебаний можно судить также и по величине относительного демпфирования (корневому показателю колебательности) , которая равна модулю отношения вещественной части корней характеристического уравнения (3.13) к их мнимой части, т.е.

.

С учетом равенства (3.14) величину относительного демпфирования можно выразить через коэффициенты характеристического уравнения звена (3.13)

,

а приняв во внимание (3.32), установить связь между и :

.

Объективно интенсивность затухания колебаний в колебательном звене определяется относительным уменьшением соседних амплитуд и переходной характеристики (рис. 3.8), оцениваемое с помощью показателя

. (3.19)

Рис. 3.8. Определение показателя по переходной характеристике звена.

Этот показатель получил название степени затухания колебаний. С учетом того, что (где - период собственных колебаний), формулу (3.19) можно представить следующим образом:

. (3.20)

Таким образом, степень затухания однозначно связана с величиной относительного демпфирования , а, следовательно, и с частотным показателем колебательности .