Тема 7
1. Укажите показатели безотказности СДМ.
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, параметр потока отказов;
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, средний ресурс;
- гамма-процентный ресурс, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, средний ресурс;
- гамма-процентный ресурс, гамма- процентный срок службы, средний срок службы, средний ресурс;
- гамма-процентный ресурс, гамма- процентный срок службы, средний срок службы, интенсивность отказов, средний ресурс.
2. Укажите показатели сохраняемости СДМ.
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, параметр потока отказов;
- вероятность восстановления, среднее время восстановления, интенсивность восстановления;
- вероятность восстановления, среднее время восстановления, интенсивность восстановления, интенсивность отказов, средний ресурс;
- гамма-процентный срок сохраняемости, средний срок сохраняемости;
- гамма-процентный срок сохраняемости, средний срок сохраняемости, вероятность восстановления, среднее время восстановления.
3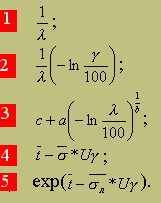
.
Укажите формулу
для определения гамма-процентного
ресурса при экспоненциальном законе
распределения.
- 1
- 2
- 3
- 4
- 5
<ris6_6.gif>
4. Как связаны между собой вероятность возникновения отказов Q(t) и вероятность безотказной работы P(t)?
- Q(t) + P(t) = 1;
- Q(t) * P(t) = 1;
- Q(t) / P(t) = 1;
- Q(t) - P(t) = 1;
- Q(t) + P(t) = 0.
5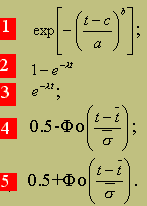
.
Укажите формулу
для определения вероятности безотказной
работы при экспоненциальном законе
распределения.
- 1
- 2
- 3
- 4
- 5 <ris6_7.gif>
6. Укажите показатели долговечности СДМ.
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, параметр потока отказов;
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, средний ресурс;
- гамма-процентный ресурс, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, средний ресурс;
- гамма-процентный ресурс, гамма- процентный срок службы, средний срок службы, средний ресурс;
- гамма-процентный ресурс, гамма- процентный срок службы, средний срок службы, интенсивность отказов, средний ресурс.
7. Укажите показатели, применяемые для оценки безотказности невосстанавливаемых элементов.
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, параметр потока отказов;
- вероятность безотказной работы, средняя наработка до отказа, интенсивность отказов;
- средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов;
- вероятность безотказной работы, средняя наработка на отказ, параметр потока отказов;
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ.
8. Укажите формулу для определения гамма-процентного ресурса при нормальном законе распределения.
- 1
- 2
- 3
- 4
- 5 <ris6_6.gif>
9. Укажите формулу для определения вероятности безотказной работы при нормальном законе распределения.
- 1
- 2
- 3
- 4
- 5
<ris6_7.gif>
10. Укажите формулу для определения интенсивности отказов.
- 1 - F(t);
- f(t)/P(t);
- P(t)/f(t);
- F(t)/P(t);
- P(t)/F(t).
11. Укажите показатели ремонтопригодности СДМ.
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, параметр потока отказов;
- вероятность восстановления, среднее время восстановления, интенсивность восстановления;
- вероятность восстановления, среднее время восстановления, интенсивность восстановления, интенсивность отказов, средний ресурс;
- гамма-процентный срок сохраняемости, средний срок сохраняемости;
- гамма-процентный срок сохраняемости, средний срок сохраняемости, вероятность восстановления, среднее время восстановления.
12. Укажите показатели применяемые для оценки безотказности восстанавлимаемых элементов.
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, параметр потока отказов;
- вероятность безотказной работы, средняя наработка до отказа, интенсивность отказов;
- средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов;
- вероятность безотказной работы, средняя наработка на отказ, параметр потока отказов;
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ;
13. Укажите формулу для определения гамма-процентного ресурса при законе распределения Вейбулла.
- 1
- 2
- 3
- 4
- 5 <ris6_6.gif>
14. Укажите формулу для определения вероятности безотказной работы при законе распределения Вейбулла.
- 1
- 2
- 3
- 4
- 5 <ris6_7.gif>
15. Укажите комплексные показатели надежности СДМ.
- вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, коэффициент готовности;
- коэффициент готовности, коэффициент технического использования;
- гамма-процентный ресурс, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов, средний ресурс;
- гамма-процентный ресурс, гамма- процентный срок службы, средний срок службы, средний ресурс;
- гамма-процентный ресурс, гамма- процентный срок службы, средний срок службы, коэффициент готовности, коэффициент технического использования.
16. При каком законе распределения интенсивность отказов будет величиной постоянной?
- нормальный;
- экспоненциальный;
- Вейбулла;
- логарифмически нормальный;
- любой из перечисленных законов.
17. Укажите формулу для определения гамма-процентного ресурса при логарифмически нормальном законе распределения.
- 1
- 2
- 3
- 4
- 5 <ris6_6.gif>
1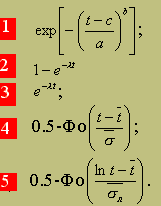
8.
Укажите формулу
для определения вероятности безотказной
работы при логарифмически нормальном
законе распределения.
- 1
- 2
- 3
- 4
- 5 <ris6_8.gif>
19. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, вычислить вероятность безотказной работы Р(t4) для t4 ч.
- 0,828;
- 0,686;
- 0,914;
- 0,086;
- 0,257.
20. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, вычислить вероятность безотказной работы Р(t3) для t3 ч.
- 0,828;
- 0,686;
- 0,914;
- 0,086;
- 0,257.
21. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, вычислить вероятность безотказной работы Р(t7) для t7 ч.
- 0,828;
- 0,686;
- 0,914;
- 0,086;
- 0,257.
22. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, вычислить вероятность отказа Q(t7) для t7 ч.
- 0,828;
- 0,686;
- 0,914;
- 0,086;
- 0,257.
23. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, вычислить вероятность отказа Q(t2) для t2 ч.
- 0,828;
- 0,686;
- 0,914;
- 0,086;
- 0,257.
24. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, вычислить вероятность отказа Q(t5) для t5 ч.
- 0,828;
- 0,543;
- 0,914;
- 0,086;
- 0,257.
25. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность безотказной работы Р(t2, t6) в интервале времени от t2 ч до t6 ч при условии, что элемент проработал безотказно t2 ч.
- (1- 0,914) / (1 – 0,172)
- (1- 0,743) / (1 – 0,086);
- (1- 0,743) / (1 – 0,314);
- (1- 0,314) / (1 – 0,086);
- (1- 0,543) / (1 – 0,172).
26. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность безотказной работы Р(t3, t9) в интервале времени от t3 ч до t9 ч при условии, что элемент проработал безотказно t3 ч.
- (1- 0,914) / (1 – 0,172)
- (1- 0,743) / (1 – 0,086);
- (1- 0,743) / (1 – 0,314);
- (1- 0,314) / (1 – 0,086);
- (1- 0,543) / (1 – 0,172).
27. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность безотказной работы Р(t4, t6) в интервале времени от t4 ч до t6 ч при условии, что элемент проработал безотказно t4 ч.
- (1- 0,914) / (1 – 0,172)
- (1- 0,743) / (1 – 0,086);
- (1- 0,743) / (1 – 0,314);
- (1- 0,314) / (1 – 0,086);
- (1- 0,543) / (1 – 0,172).
28. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность безотказной работы Р(t2, t4) в интервале времени от t2 ч до t4 ч при условии, что элемент проработал безотказно t2 ч.
- (1- 0,914) / (1 – 0,172)
- (1- 0,743) / (1 – 0,086);
- (1- 0,743) / (1 – 0,314);
- (1- 0,314) / (1 – 0,086);
- (1- 0,543) / (1 – 0,172).
29. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность безотказной работы Р(t3, t5) в интервале времени от t3 ч до t5 ч при условии, что элемент проработал безотказно t3 ч.
- (1- 0,914) / (1 – 0,172)
- (1- 0,743) / (1 – 0,086);
- (1- 0,743) / (1 – 0,314);
- (1- 0,314) / (1 – 0,086);
- (1- 0,543) / (1 – 0,172).
30. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность отказа Q(t3, t5) в интервале времени от t3 ч до t5 ч при условии, что элемент проработал безотказно t3 ч.
- 1 - [(1- 0,914) / (1 – 0,172)]
- 1 - [(1- 0,743) / (1 – 0,086)];
- 1 - [(1- 0,743) / (1 – 0,314)];
- 1 - [(1- 0,314) / (1 – 0,086)];
- 1 – [(1- 0,543) / (1 – 0,172)].
31. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
Приняв эмпирическую функцию в качестве истинной, определить вероятность отказа Q(t2, t4) в интервале времени от t2 ч до t4 ч при условии, что элемент проработал безотказно t2 ч.
- 1 - [(1- 0,914) / (1 – 0,172)]
- 1 - [(1- 0,743) / (1 – 0,086)];
- 1 - [(1- 0,743) / (1 – 0,314)];
- 1 - [(1- 0,314) / (1 – 0,086)];
- 1 – [(1- 0,543) / (1 – 0,172)].
32. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность отказа Q(t4, t6) в интервале времени от t4 ч до t6 ч при условии, что элемент проработал безотказно t4 ч.
- 1 - [(1- 0,914) / (1 – 0,172)]
- 1 - [(1- 0,743) / (1 – 0,086)];
- 1 - [(1- 0,743) / (1 – 0,314)];
- 1 - [(1- 0,314) / (1 – 0,086)];
- 1 – [(1- 0,543) / (1 – 0,172)].
33. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность отказа Q(t2, t6) в интервале времени от t2 ч до t6 ч при условии, что элемент проработал безотказно t2 ч.
- 1 - [(1- 0,914) / (1 – 0,172)]
- 1 - [(1- 0,743) / (1 – 0,086)];
- 1 - [(1- 0,743) / (1 – 0,314)];
- 1 - [(1- 0,314) / (1 – 0,086)];
- 1 – [(1- 0,543) / (1 – 0,172)].
34. По результатам испытаний N =35 элементов для моментов времени ti,ч построена эмпирическая функция распределения F(ti):
ti 1 2 3 4 5 6 7 8 9
F(ti) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
Приняв эмпирическую функцию в качестве истинной, определить вероятность отказа Q(t3, t9) в интервале времени от t2 ч до t6 ч при условии, что элемент проработал безотказно t2 ч.
- 1 - [(1- 0,914) / (1 – 0,172)]
- 1 - [(1- 0,743) / (1 – 0,086)];
- 1 - [(1- 0,743) / (1 – 0,314)];
- 1 - [(1- 0,314) / (1 – 0,086)];
- 1 – [(1- 0,543) / (1 – 0,172)].
35. Пусть при испытаниях N =35 элементов фиксировалось число произошедших отказов n(ti) в моменты времени ti,ч:
t1 = 1; t2 =2 t3= 3; t4= 4; t5= 5; t6=6; t7= 7; t8= 8; t9= 9.
Число отказов, n(ti):
n(t1)=0; n(t2)=3; n(t3)=3; n(t4)=5; n(t5)=8; n(t6)=7; n(t7)=6; n(t8)=2; n(t9)=1.
Определите значение статистической оценки интенсивности отказов ?(t4)в момент времени t4.
- 3/(35-3);
- 5/(35-6);
- 8/(35-11);
- 6/(35-26);
- 3/35.
36. Пусть при испытаниях N =35 элементов фиксировалось число произошедших отказов n(ti) в моменты времени ti,ч:
t1 = 1; t2 =2 t3= 3; t4= 4; t5= 5; t6=6; t7= 7; t8= 8; t9= 9.
Число отказов, n(ti):
n(t1)=0; n(t2)=3; n(t3)=3; n(t4)=5; n(t5)=8; n(t6)=7; n(t7)=6; n(t8)=2; n(t9)=1.
Определите значение статистической оценки интенсивности отказов ?(t3)в момент времени t3.
- 3/(35-3);
- 5/(35-6);
- 8/(35-11);
- 6/(35-26);
- 3/35.
37. Пусть при испытаниях N =35 элементов фиксировалось число произошедших отказов n(ti) в моменты времени ti,ч:
t1 = 1; t2 =2 t3= 3; t4= 4; t5= 5; t6=6; t7= 7; t8= 8; t9= 9.
Число отказов, n(ti):
n(t1)=0; n(t2)=3; n(t3)=3; n(t4)=5; n(t5)=8; n(t6)=7; n(t7)=6; n(t8)=2; n(t9)=1.
Определите значение статистической оценки интенсивности отказов ?(t5)в момент времени t5.
- 3/(35-3);
- 5/(35-6);
- 8/(35-11);
- 6/(35-26);
- 3/35.
38. Пусть при испытаниях N =35 элементов фиксировалось число произошедших отказов n(ti) в моменты времени ti,ч:
t1 = 1; t2 =2 t3= 3; t4= 4; t5= 5; t6=6; t7= 7; t8= 8; t9= 9.
Число отказов, n(ti):
n(t1)=0; n(t2)=3; n(t3)=3; n(t4)=5; n(t5)=8; n(t6)=7; n(t7)=6; n(t8)=2; n(t9)=1.
Определите значение статистической оценки интенсивности отказов ?(t7)в момент времени t7.
- 3/(35-3);
- 5/(35-6);
- 8/(35-11);
- 6/(35-26);
- 3/35.
39. Пусть при испытаниях N =35 элементов фиксировалось число произошедших отказов n(ti) в моменты времени ti,ч:
t1 = 1; t2 =2 t3= 3; t4= 4; t5= 5; t6=6; t7= 7; t8= 8; t9= 9.
Число отказов, n(ti):
n(t1)=0; n(t2)=3; n(t3)=3; n(t4)=5; n(t5)=8; n(t6)=7; n(t7)=6; n(t8)=2; n(t9)=1.
Определите значение статистической оценки интенсивности отказов ?(t2)в момент времени t2.
- 3/(35-3);
- 5/(35-6);
- 8/(35-11);
- 6/(35-26);
- 3/35
40. В течение некоторого периода проводилось наблюдение за работой одной машины. За весь период наблюдений было зарегистрировано 20 отказов. До начала наблюдений машина проработала 200 часов, к концу наблюдений 1000 часов. Определить среднюю наработку на отказ.
- 60;
- 50;
- 10;
- 40;
- 30
41. В течение некоторого периода проводилось наблюдение за работой одной машины. За весь период наблюдений было зарегистрировано 20 отказов. До начала наблюдений машина проработала 200 часов, к концу наблюдений 1000 часов. Определить осредненный параметр потока отказов.
- 0,030;
- 0,020;
- 0,01;
- 0,025;
- 0,04
42. Машина имеет среднюю наработку на отказ 50 часов и среднее время восстановления 1 час. Определить коэффициент готовности.
- (50+1)/(50-1);
- (50-1)/50;
- 50/(50-1);
- 50/(50+1);
- (50+1)/50
43. Время восстановления элемента является случайной величиной, принимающей значение t1 = 0,1 ч с вероятностью p1 = 0,6, значение t2 = 0,2 ч с вероятностью р2 = 0,3 и значение t3 = 1,5 ч с вероятностью р3 = 0,1. Определить среднее время восстановления элемента
- 0,027
- 0,1
- 0,2
- 0,27
- 1,5
44. Пусть закон распределения времени работы элемента до отказа является нормальным, параметры которого а =100 ч и ?= 30 ч. Требуется вычислить среднее время наработки до отказа?
- 3000
- 3
- 0,3
- 100
- 30
45.Пусть элемент имеет экспоненциальные законы распределения времени работы до отказа и времени восстановления с параметрами соответственно λ = 0,04 1/ч и µ = 2 1/ч. Требуется вычислить среднее время наработки до отказа?
- 0,5
- 2/(2 + 0,04),
- 0,04/(2 + 0,04)
- 25
- 2
46.Пусть элемент имеет экспоненциальные законы распределения времени работы до отказа и времени восстановления с параметрами соответственно λ = 0,04 1/ч и µ = 2 1/ч. Требуется вычислить среднее время восстановления?
- 0,5
- 2/(2 + 0,04),
- 0,04/(2 + 0,04)
- 25
- 2
47.Пусть элемент имеет экспоненциальные законы распределения времени работы до отказа и времени восстановления с параметрами соответственно λ = 0,04 1/ч и µ = 2 1/ч. Требуется вычислить коэффициент готовности?
- 0,5
- 2/(2 + 0,04),
- 0,04/(2 + 0,04)
- 25
- 2
48.Пусть элемент имеет экспоненциальные законы распределения времени работы до отказа и времени восстановления с параметрами соответственно λ = 0,04 1/ч и µ = 2 1/ч. Требуется вычислить интенсивность отказов?
- 0,5
- 1
- 0,04
- 25
- 2
49.Пусть элемент имеет экспоненциальные законы распределения времени работы до отказа и времени восстановления с параметрами соответственно λ = 0,04 1/ч и µ = 2 1/ч. Требуется вычислить интенсивность восстановления?
- 0,5
- 1
- 0,04
- 25
- 2
Тема 8
1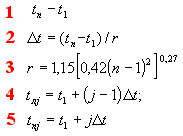
.
По какой формуле
определяют размах выборки случайных
величин?
- 1
- 2
- 3
- 4
- 5 <t7_r1.gif>
2. По какой формуле определяют ширину интервалов группирования случайных величин?
- 1
- 2
- 3
- 4
- 5 <t7_r1.gif>
3. По какой формуле определяют число интервалов группирования случайных величин?
- 1
- 2
- 3
- 4
- 5 <t7_r1.gif>
4. По какой формуле определяют левую границу J-го интервала группирования случайных величин?
- 1
- 2
- 3
- 4
- 5 <t7_r1.gif>
5. По какой формуле определяют правую границу J-го интервала группирования случайных величин?
- 1
- 2
- 3
- 4
- 5 <t7_r1.gif>
6
.
По какой формуле
определяют частость (вероятность)
попадания случайных величин на J-ый
интервал?
- 1
- 2
- 3
- 4
- 5 <t7_r2.gif>
7. По какой формуле определяют значение эмпирической плотности вероятностей распределения случайных величин на J-ом интервале?
- 1
- 2
- 3
- 4
- 5 <t7_r2.gif>
8. В результате наблюдения за работой машины получена выборка случайных значений наработок машины до первого отказа: 7.5, 92.3, 51.4, 30.7, 102.3, 34.9, 22.5, 42.3, 54.7, 45.8, 45.0, 114.5, 36.2, 16.2, 41.4, 121.2, 12.7, 36.2, 21.9, 53.1, 187.5, 18.5, 163.0, 64.4. Определите объем выборки n?
- 24;
- 12;
- 30;
- 7.5
- 180
9. В результате наблюдения за работой машины получена выборка случайных значений наработок машины до первого отказа: 7.5, 92.3, 51.4, 30.7, 102.3, 34.9, 22.5, 42.3, 54.7, 45.8, 45.0, 114.5, 36.2, 16.2, 41.4, 121.2, 12.7, 36.2, 21.9, 53.1, 187.5, 18.5, 163.0, 64.4. Определите размах выборки n?
- 24;
- 12;
- 30;
- 7.5
- 180
10. В результате наблюдения за работой машины получена выборка случайных значений наработок машины до первого отказа: 7.5, 92.3, 51.4, 30.7, 102.3, 34.9, 22.5, 42.3, 54.7, 45.8, 45.0, 114.5, 36.2, 16.2, 41.4, 121.2, 12.7, 36.2, 21.9, 53.1, 187.5, 18.5, 163.0, 64.4. Определите ширину интервалов группирования, если число интервалов r = 6?
- 24;
- 12;
- 30;
- 7.5
- 180
11. В результате наблюдения за работой машины получена выборка случайных значений наработок машины до первого отказа: 7.5, 92.3, 51.4, 30.7, 102.3, 34.9, 22.5, 42.3, 54.7, 45.8, 45.0, 114.5, 36.2, 16.2, 41.4, 121.2, 12.7, 36.2, 21.9, 53.1, 187.5, 18.5, 163.0, 64.4. Определите левую - tл и правую - tп границы первого интервала, если число интервалов r = 6?
- tл = 7.5; tп = 47.5;
- tл = 7.5; tп = 57.5;
- tл = 7.5; tп = 27.5;
- tл = 7.5; tп = 37.5;
- tл = 7.5; tп = 17.5
12. В результате наблюдения за работой машины получена выборка случайных значений наработок машины до первого отказа:7.5, 92.3, 51.4, 30.7, 102.3, 34.9, 22.5, 42.3, 54.7, 45.8, 45.0, 114.5, 36.2, 16.2, 41.4, 121.2, 12.7, 36.2, 21.9, 53.1, 187.5, 18.5, 163.0, 64.4. Определите частоту (количество случайных значений до первого отказа) попадания случайных величин в первый интервал, если границы интервала tл = 7.5; tп = 37.5?
- 24;
- 12;
- 10;
- 15
- 18
13. В результате наблюдения за работой машины получена выборка случайных значений наработок машины до первого отказа:7.5, 92.3, 51.4, 30.7, 102.3, 34.9, 22.5, 42.3, 54.7, 45.8, 45.0, 114.5, 36.2, 16.2, 41.4, 121.2, 12.7, 36.2, 21.9, 53.1, 187.5, 18.5, 163.0, 64.4. Определите частость (вероятность) попадания случайных величин в первый интервал, если границы интервала tл = 7.5; tп = 37.5?
- 24/24;
- 12/24;
- 10/24;
- 10/30
- 12/30
14. В результате наблюдения за работой машины получена выборка случайных значений наработок машины до первого отказа:7.5, 92.3, 51.4, 30.7, 102.3, 34.9, 22.5, 42.3, 54.7, 45.8, 45.0, 114.5, 36.2, 16.2, 41.4, 121.2, 12.7, 36.2, 21.9, 53.1, 187.5, 18.5, 163.0, 64.4. Определите значение эмпирической плотности распределения вероятностей случайных величин на первом интервале, если границы интервала tл = 7.5; tп = 37.5?
- 24/(24*30);
- 12/(24*30);
- 10/(24*30);
- 10/(30*30)
- 12/(30*30)
15. Чем является гистограмма?
- статистическим аналогом теоретической плотности распределения (эмпирической плотностью распределения;
- статистическим аналогом функции распределения;
- теоретической плотностью распределения;
- теоретической функцией распределения;
- числовой характеристикой случайной величины.
16. Чему равна площадь гистограммы?
- 1
- 2
- 3
- 4
- 0,5
17. Что представляет собой площадь гистограммы?
- вероятность;
- плотность вероятностей;
- случайную величину;
- вероятность и плотность вероятностей;
- вероятность и случайную величину.
1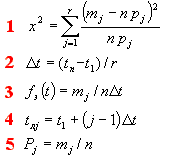
8.
По какой формуле
определяют критерий согласия Пирсона?
- 1
- 2
- 3
- 4
- 5 <t7_r3.gif>
19. При какой частоте mj соседние интервалы объединяются для расчета критерия согласия Пирсона (в условиях выполняемых лабораторных работ)?
- mj < 5
- mj > 5
- mj = 5
- mj > 10
-
mj > 15
20. По какой формуле вычисляют число степеней свободы для определения табличного значения критерий согласия Пирсона?
- 1
- 2
- 3
- 4
- 5 <t7_r4.gif>
21. Определите число степеней свободы для определения табличного значения критерий согласия Пирсона, если число интервалов с учетом их объединения r0 =8, а предполагаемый закон распределения - экспоненциальный?
- 6
- 4
- 7
- 5
- 8
22. Определите число степеней свободы для определения табличного значения критерий согласия Пирсона, если число интервалов с учетом их объединения r0 =8, а предполагаемый закон распределения - нормальный?
- 6
- 4
- 7
- 5
- 8
23. Определите число степеней свободы для определения табличного значения критерий согласия Пирсона, если число интервалов с учетом их объединения r0 =8, а предполагаемый закон распределения - Вейбулла?
- 6
- 4
- 7
- 5
- 8
24. Определите число степеней свободы для определения табличного значения критерий согласия Пирсона, если число интервалов с учетом их объединения r0 =8, а предполагаемый закон распределения - логарифмически нормальный?
- 6
- 4
- 7
- 5
- 8
25. В каком случае гипотеза о согласии опытного и теоретического распределения принимается?
- если рассчитанное значение критерия Пирсона меньше табличного значения критерия Пирсона при данной доверительной вероятности;
- если рассчитанное значение критерия Пирсона больше табличного значения критерия Пирсона при данной доверительной вероятности;
- если коэффициент вариации равен 0,3;
- если коэффициент вариации равен 1;
- если коэффициент вариации больше 1 χ2
26. При подборе теоретического распределения получены следующие значения рассчитанного и табличного критерия Пирсона:
экспоненциальное - χ2 =3; (χ*)2= 10,6;
нормальное - χ2 =8,1; = 7,8;
логарифмически нормальное - χ2 =8,8; (χ*)2= 7,8;
Вейбулла - χ2 =10,1; (χ*)2= 9,2.
Какое распределение будет принято?
- экспоненциальное
- нормальное
- логарифмически нормальное
- Вейбулла
- никакое
27. При подборе теоретического распределения получены следующие значения рассчитанного и табличного критерия Пирсона:
экспоненциальное - χ2 =3; (χ*)2= 10,6;
нормальное - χ2 =8,1; = 7,8;
логарифмически нормальное - χ2 =8,8; (χ*)2= 7,8;
Вейбулла - χ2 =10,1; (χ*)2= 9,2.
Какое распределение будет принято?
- экспоненциальное
- нормальное
- логарифмически нормальное
- Вейбулла
- никакое
Тема 9
1. Какой документ, устанавливает комплекс взаимосвязанных организационно-технических требований и мероприятий, подлежащих проведению на определенных стадиях жизненного цикла объекта и направленных на обеспечение заданных требований к надежности и (или) на повышение надежности?
- техническое задание;
- технический проект;
- программа обеспечения надежности;
- рабочий проект;
- техническое предложение
2. Укажите последний этап, входящий в программу обеспечения надежности?
- подтверждение показателей надежности серийно выпускаемых ТС;
- обоснование требований к надежности элементов подсистем первого уровня;
- обеспечение требований к надежности элементов ТС при разработке рабочего проекта;
- обоснование требований к надежности ТС и ее подсистемам первого уровня
- обеспечение требований к надежности ТС при ресурсных испытаниях ее элементов
3. Как идет обоснование требований к надежности ТС?
- от ТС к ее элементам;
- от элементов к ТС;
- не имеет значения;
- зависит от решения проектировщика;
- зависит от типа ТС
4. Как идет обеспечение требований к надежности ТС?
- от ТС к ее элементам;
- от элементов к ТС;
- не имеет значения;
- зависит от решения проектировщика;
- зависит от типа ТС
5. На каком этапе проектирования выполняется обоснование требований к надежности ТС и ее подсистемам первого уровня?
- при разработке технического задания, технического предложения или эскизного проекта;
- при разработке технического проекта;
- при разработке рабочего проекта;
- в период подготовки ТС к приемочным испытаниям;
- при разработке технического проекта или рабочего проекта
6. На каком этапе проектирования выполняется обоснование требований к надежности элементов подсистем первого уровня?
- при разработке технического задания или эскизного проекта;
- при разработке технического проекта;
- при разработке рабочего проекта;
- в период подготовки ТС к приемочным испытаниям;
- при подготовке технического предложения
7. На каком этапе проектирования выполняется обеспечение требований к надежности элементов ТС?
- при разработке технического задания или эскизного проекта;
- при разработке технического проекта;
- при разработке рабочего проекта и при ресурсных испытаниях в период подготовки ТС к приемочным испытаниям;
- при разработке технического и рабочего проектов;
- при подготовке технического предложения
8. Укажите факторы, влияющие на выбор номенклатуры показателей надежности машины?
- ремонтируемая или неремонтируемая; временной режим использования; принцип ограничения длительности эксплуатации, стоимость машины;
- ремонтируемая или неремонтируемая; временной режим использования; принцип ограничения длительности эксплуатации; факторы последствий отказов;
- техническая характеристика; временной режим использования; принцип ограничения длительности эксплуатации; факторы последствий отказов;
- техническая характеристика; временной режим использования; принцип ограничения длительности эксплуатации; стоимость машины;
- ремонтируемая или неремонтируемая; временной режим использования; принцип ограничения длительности эксплуатации; техническая характеристика.
9. Укажите факторы последствий отказов для СДМ третьей группы (экскаваторы, бульдозеры, скреперы и т.д.)?
- факт достижения предельного состояния;
- факт наличия отказа;
- нет правильного ответа;
- наличие отказа и вынужденный простой;
- факт вынужденного простоя;
1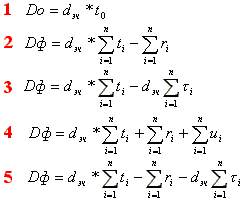
0.
По какой формуле
определяют доход от использования
машины, если она не имеет отказов?
- 1
- 2
- 3
- 4
- 5 <t10_r1.gif>
11. По какой формуле определяют доход от использования машины, если доминирующим фактором последствий отказа является сам факт отказа?
- 1
- 2
- 3
- 4
- 5 <t10_r1.gif>
12. По какой формуле определяют доход от использования машины, если доминирующим фактором последствий отказа является вынужденный простой в ремонте?
- 1
- 2
- 3
- 4
- 5 <t10_r1.gif>
13. По какой формуле определяют доход от использования машины, если доминирующим фактором последствий отказа является факт отказа и вынужденный простой в ремонте?
- 1
- 2
- 3
- 4
- 5 <t10_r1.gif>
1
4.
Какие показатели надежности ТС позволяет
определить первый член уравнения
фактического дохода от ее эксплуатации?
- ресурс и наработку на отказ;
- среднюю суммарную стоимость ремонтов;
- среднее время восстановления;
- ресурс и среднее время восстановления;
- наработку на отказ и среднее время восстановления. <t10_r2.gif>
1
5.
Какие показатели надежности ТС позволяет
определить второй член уравнения
фактического дохода от ее эксплуатации?
- ресурс и наработку на отказ;
- среднюю суммарную стоимость ремонтов;
- среднее время восстановления;
- ресурс и среднее время восстановления;
- наработку на отказ и среднее время восстановления.
<t10_r3.gif>
16. Какие показатели надежности ТС позволяет определить второй член уравнения фактического дохода от ее эксплуатации?
- ресурс и наработку на отказ;
- среднюю суммарную стоимость ремонтов;
- среднее время восстановления;
- ресурс и среднее время восстановления;
- наработку на отказ и среднее время восстановления.
Тема 10
1. Укажите критерии отказов двигателя.
- повреждение блока цилиндров, устранимое без полной разборки двигателя; предельный износ шеек коленчатого вала;
- снижение мощности ниже допустимой; повреждение блока цилиндров, устранимое без полной разборки; давление впрыскивания форсунки за пределами допустимого;
- снижение мощности ниже допустимой; повреждение блока цилиндров, устранимое без полной разборки двигателя; предельный износ шеек коленчатого вала;
- предельный износ шеек коленчатого вала; расход картерных газов превышает допустимое значение;
- расход картерных газов превышает допустимое значение; повреждение блока цилиндров, устранимое без полной разборки двигателя.
2. Укажите критерии предельного состояния двигателя.
- повреждение блока цилиндров, устранимое без полной разборки двигателя; давление впрыскивания форсунки за пределами допустимого;
- снижение мощности ниже допустимой; повреждение блока цилиндров, устранимое без полной разборки двигателя;
- снижение мощности ниже допустимой; давление впрыскивания форсунки за пределами допустимого; предельный износ шеек коленчатого вала;
- предельный износ шеек коленчатого вала; расход картерных газов превышает допустимое значение;
- предельный износ шеек коленчатого вала; повреждение блока цилиндров, устранимое без полной разборки двигателя.
3. По каким признакам устанавливают критерии отказов ТС?
- по одному отличительному признаку или по совокупности признаков неработоспособного состояния;
- по таким отличительным признакам, на основании которых следует считать невозможным дальнейшее использование ТС;
- по одному отличительному признаку или по совокупности признаков работоспособного состояния;
- по одному отличительному признаку или по совокупности признаков неисправного состояния;
- по одному отличительному признаку или по совокупности признаков исправного состояния;
4. По каким признакам устанавливают критерии предельного состояния ТС?
- по одному отличительному признаку или по совокупности признаков неработоспособного состояния;
- по таким отличительным признакам, на основании которых следует считать невозможным дальнейшее использование ТС;
- по одному отличительному признаку или по совокупности признаков работоспособного состояния;
- по одному отличительному признаку или по совокупности признаков неисправного состояния;
- по одному отличительному признаку или по совокупности признаков исправного состояния;
5. Укажите причины при которых дальнейшая эксплуатация ТС невозможна или нецелесообразна?
- неустранимое нарушения требований безопасности, недопустимое снижение эффективности эксплуатации, необходимость проведения капитального ремонта;
- устранимое нарушения требований безопасности, недопустимое снижение эффективности эксплуатации, необходимость проведения капитального ремонта;
- неустранимое нарушения требований безопасности, устранимый выход функциональных параметров за допускаемые пределы;
- неустранимое нарушения требований безопасности, допустимое снижение эффективности эксплуатации, необходимость проведения капитального ремонта;
- неустранимое нарушения требований безопасности, недопустимое снижение эффективности эксплуатации, нет необходимости проведения капитального ремонта;
6. Укажите признаки предельного состояния ТС?
- достижение ТС ресурса до КР; отклонение функционального параметра за пределы норм, не приводящее к недопустимому снижению эффективности эксплуатации;
- достижение ТС назначенного ресурса до КР; отклонение функционального параметра за пределы норм, приводящее к недопустимому снижению эффективности эксплуатации;
- отклонение функционального параметра за пределы норм, не приводящее к недопустимому снижению эффективности;
- отказ элемента ТС, приводящий к отказу всей ТС;
- достижение ТС назначенного ресурса до капитального ремонта; отказ элемента ТС, приводящий к отказу всей ТС
7. Укажите признаки отказов ТС?
- достижение ТС назначенного ресурса до КР; отклонение функционального параметра за пределы норм, приводящее к недопустимому снижению эффективности эксплуатации;
- достижение ТС назначенного ресурса до КР; отклонение функционального параметра за пределы норм,не приводящее к недопустимому снижению эффективности;
- отклонение функционального параметра за пределы норм,не приводящее к недопустимому снижению эффективности;отказ элемента,приводящий к отказу всей ТС;
- отклонение функционального параметра за пределы норм,приводящее к недопустимому снижению эффективности;отказ элемента,приводящий к отказу всей ТС;
- достижение ТС назначенного ресурса до капитального ремонта; отказ элемента ТС, приводящий к отказу всей ТС