
Міністерство освіти і науки,
Херсонський політехнічний коледж
Одеського національного політехнічного університету
(базовий ВНЗ І–ІІ р. а. Херсонської області)
Розглянуто
На засіданні циклової
Комісії математики 2013
«Затверджую»
Заст. Директора
з навчальної роботи
__________А.М. Дудніков
__________ 2013
методичні вказівки та завдання
з теми «прямі та площини у просторі»
Херсон 2013
«Погоджено»
Зав. метод кабінетом
2013р.
Методичні вказівки та завдання з мети «Прямі та площини у просторі» [Текст] / Херсон. політехн. коледж Одес. нац. політехн. ун‑т; уклад.: С. В. Рослякова, О. В. Кузякіна. – Херсон : ХПТК ОНПУ, 2013. – 34 с.
Навчальне видання
методичні вказівки та завдання з теми «Прямі та площини у просторі»
Укладачі: |
Рослякова Світлана Володимирівна, спеціаліст вищої категорії, викладач-методист Кузякіна Ольга Володимирівна, спеціаліст другої категорії, викладач
|
Коректор |
Г.Ф. Сафонова, спеціаліст вищої категорії, викладач |
Зміст
Передмова………………………………………………………. 4
Теоретичні відомості з курсу планіметрії …………..…6
Розв’язування типових задач……………………….....13
Задачі по даній темі …………………………….……...16
Рисунки до задач ……………………………................31
Відповіді до задач……………………………………...34
Список рекомендованої літератури …………………..35
Передмова
Задачник-практикум з геометрії призначений для студентів першого курсу. Мета збірника – допомогти студенту в засвоєнні практичної частини теми «Прямі та площини в просторі» та оволодіти методами розв’язування задач.
В збірнику міститься мінімальне число задач які потрібен розв’язувати студент по закінченню вивчення теми. Приведено зразки запису розв’язків задач та малюнки до задач, що допомагають приступити до розв’язку.
Перш ніж приступити до розв’язку задач студент повинен вивчити відповідний теоретичний матеріал.
Приступаючи до розв’язку задач, слід намагатися самотужки виконати малюнок, а потім порівняти з тим що міститься в збірнику.
Розпочинаючи розв’язування стереометричних задач, слід враховувати деякі особливості, пов’язані з тим, що в стереометричних задачах розглядаються просторові тіла, а не плоскі фігури. Зокрема, при розв’язуванні стереометричних задач на обчислення найчастіше спочатку доводиться обґрунтовувати якусь властивість заданої конфігурації або тіла і тільки після того, як цю властивість установлено, може бути виконано обчислювальну частину задачі.
Рисунок стереометричної задачі, це плоске зображення просторових об’єктів. Точки та просторові прямі зображуються на малюнку точками та прямими, а площини, сфери та інші поверхні доводиться уявляти, маючи лише зображення їх окремих елементів. Інколи для розв’язку задачі можна виносити на окремий малюнок якийсь переріз тіла.
По суті розв’язок стереометричної задачі зводиться до розв’язання ряду планіметричних задач. Відомо, що одна й та же задача часто допускає різні способи розв’язку, тому віднесення задачі до того чи іншого методу чисто умовне.
Слід при розв’язанні задач звернути увагу на порядок оформлення. Для цього в збірнику приведено зразки розв’язків. Всі задачі що внесені до збірника допомагають студентам набути навичок практичного застосування теоретичних знань.
Теоретичні відомості з курсу планіметрії
1.
Прямокутний
трикутник(a,
b-
катети;
c
– гіпотенуза;
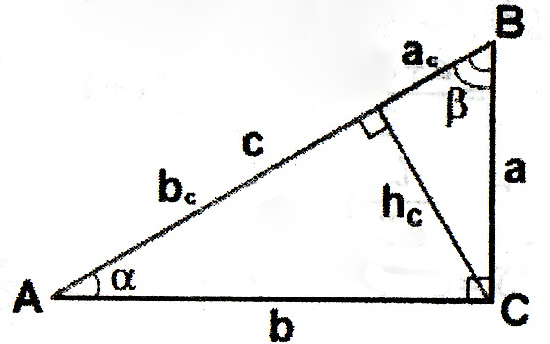
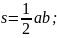
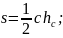

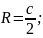
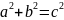 — теорема
Піфагора.
— теорема
Піфагора.

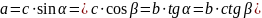
2. Рівнобічний трикутник (a- довжинасторони; r- радіус вписаного кола; S- площа; R- радіус описаного кола):
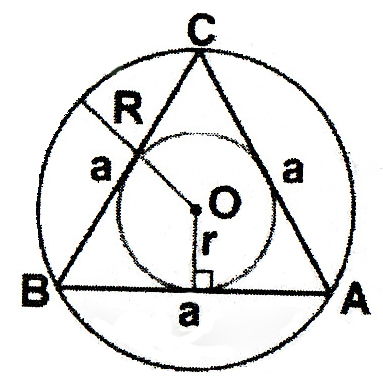
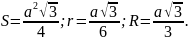
3.
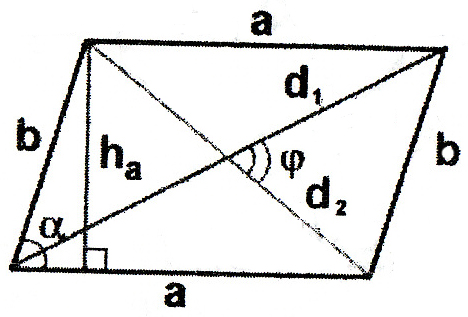
Паралелограм
(a
і
b
– суміжні
сторони;
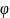 – кут між
ними;
– кут між
ними;
 –
висота,
яка проведена до сторони a):
–
висота,
яка проведена до сторони a):
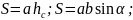
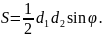
Ромб:
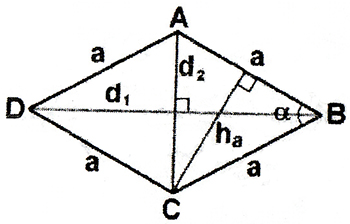
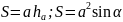 ;
;
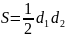
Прямокутник:
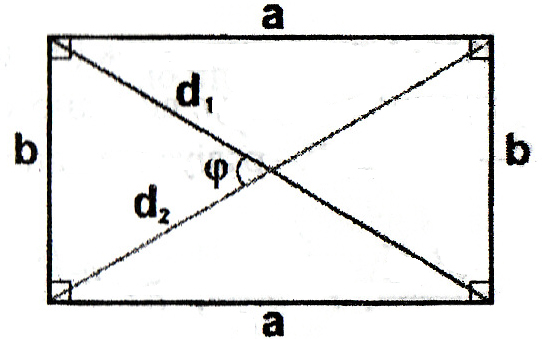
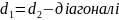 ;
;
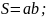
К
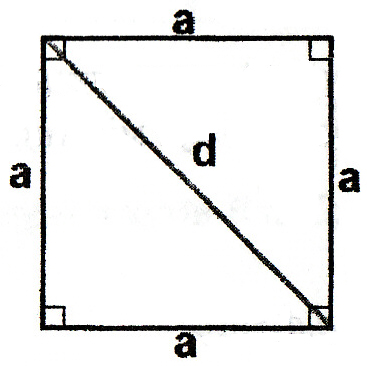 вадрат
(d-
діагональ):
вадрат
(d-
діагональ):
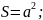

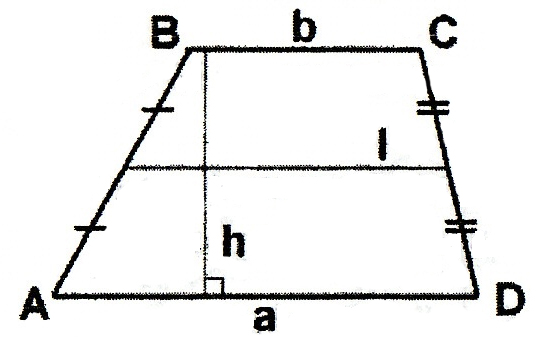
Трапеція (a і b – основи; h- відстань між ними; l – середня лінія):
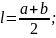
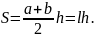
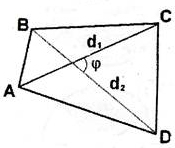
Довільний чотирикутник (
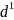 і
і
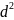 – діагоналі;
-
кут між ними; S-
площа):
– діагоналі;
-
кут між ними; S-
площа):
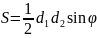
Описаний многокутник (p – півпериметр; r- радіус вписаного кола):
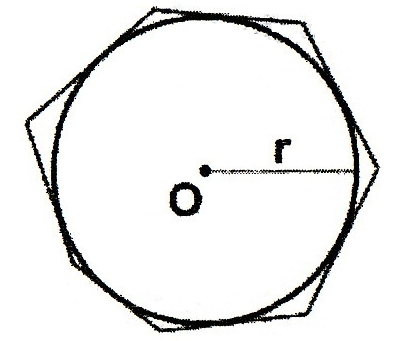
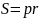
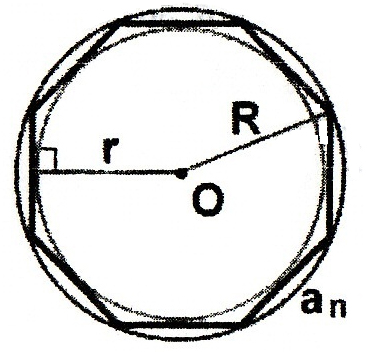
Правильний многокутник (
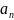 -
сторона правильного n-кутника;
R-
радіус
описаного кола;
r-
радіус
вписаного кола):
-
сторона правильного n-кутника;
R-
радіус
описаного кола;
r-
радіус
вписаного кола):
Довільний трикутник (довжини сторін, які лежать проти вершин А, В і С, дорівнюють а, b, с відповідно;
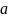 ,
,
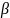 ,
,
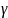 - величини кутів А,
В
і С;
р-
півпериметр; R
-
радіус описаного кола; r
- радіус вписаного кола; S
- площа; ha
- висота,
яка проведена з вершини А):
- величини кутів А,
В
і С;
р-
півпериметр; R
-
радіус описаного кола; r
- радіус вписаного кола; S
- площа; ha
- висота,
яка проведена з вершини А):
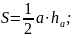
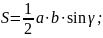
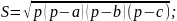
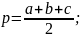
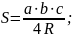
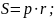
 – теорема
косинусів;
– теорема
косинусів;
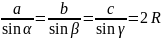 – теорема
синусів;
– теорема
синусів;
 – висота
до сторони c;
– висота
до сторони c;
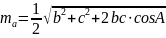 – медіана
до сторони a;
– медіана
до сторони a;
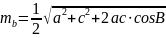 – медіана
до сторони
b;
– медіана
до сторони
b;
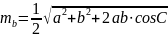 –
медіана
до сторони
с;
–
медіана
до сторони
с;
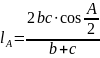 – бісектриса
кута A;
– бісектриса
кута A;
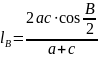 -
бісектриса
кута B;
-
бісектриса
кута B;
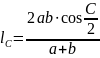 -
бісектриса
кута C.
-
бісектриса
кута C.
