6. Точки разрыва функции.

Пример 6.1. Найти точки разрыва функции 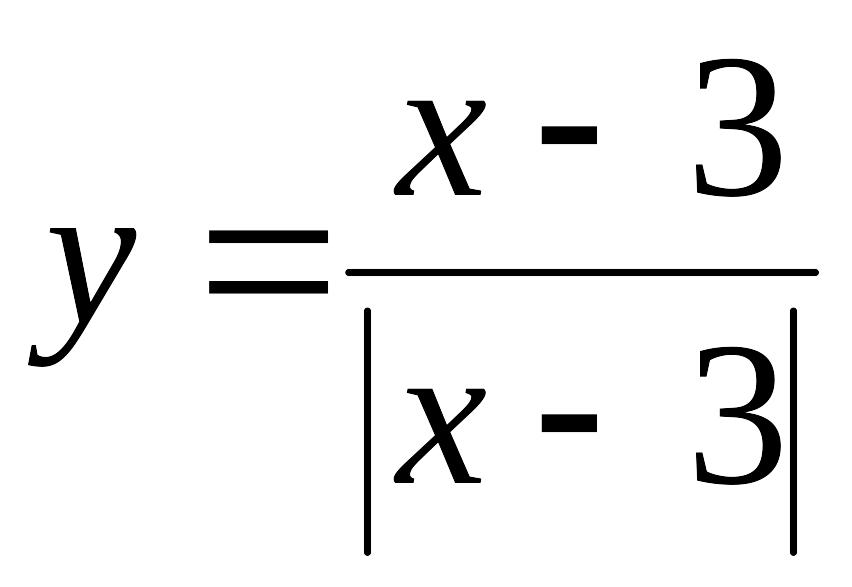и определить их характер.

Функция непрерывна при всех значениях , а в точке функция не определена. Значит – точка разрыва. Вычислим односторонние пределы функции в этой точке.

; .

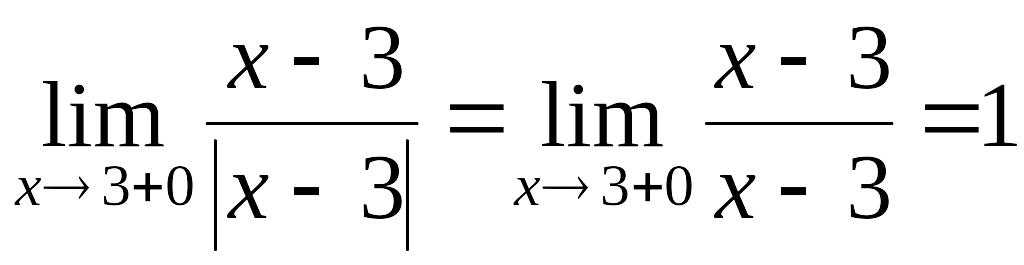Так как односторонние пределы конечны и 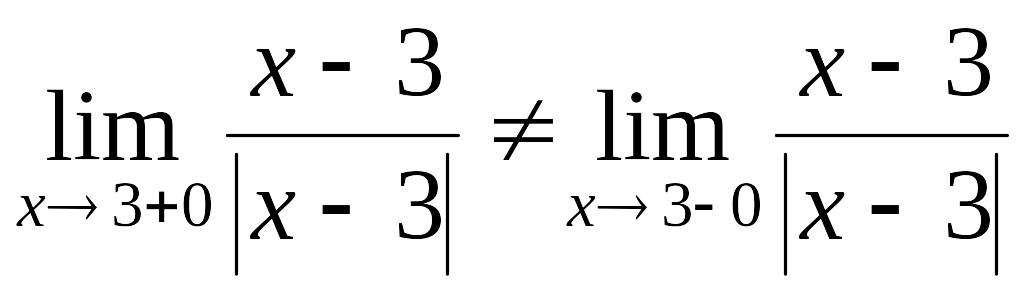, то – точка разрыва 1-го рода.

Пример 6.2. Найти точки разрыва функции и определить их характер.

Функция непрерывна при всех значениях , а в точке функция не определена. Значит – точка разрыва. Вычислим односторонние пределы в этой точке. Имеем , так как при числитель дроби стремится к 4, а знаменатель является отрицательной б.м. функцией. Далее, , так как при числитель дроби стремится к 4, а знаменатель является положительной б.м. функцией. Таким образом, односторонние пределы бесконечные, поэтому – точка разрыва 2-го рода.

Пример 6.3. Найти точки разрыва функции и определить их характер.

Функция непрерывна при всех действительных значениях х, кроме , значит, – точка разрыва. Определим её характер, для этого вычислим односторонние пределы

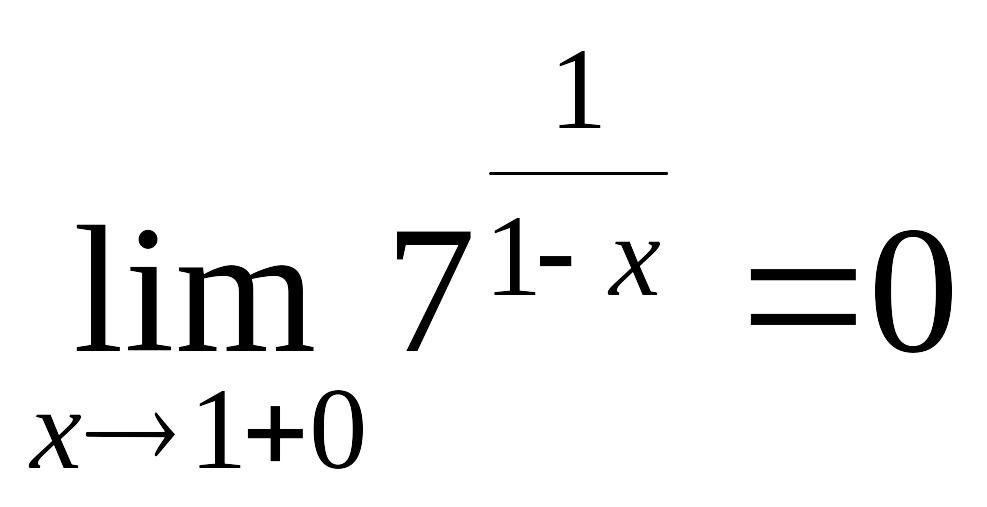, так как при ;

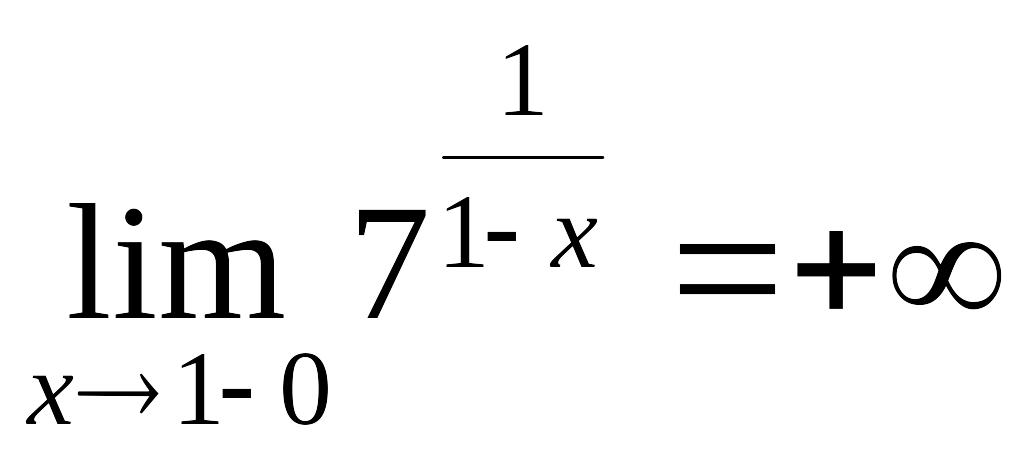, так как при .

В силу того, что один из односторонних пределов равен ∞, – точка разрыва 2-го рода.

Пример 6.4. Найти точки разрыва функции и определить их характер.

Рациональная функция непрерывна во всех точках за исключением тех, в которых знаменатель обращается в нуль, а именно, в точках .

Рассмотрим точку . Найд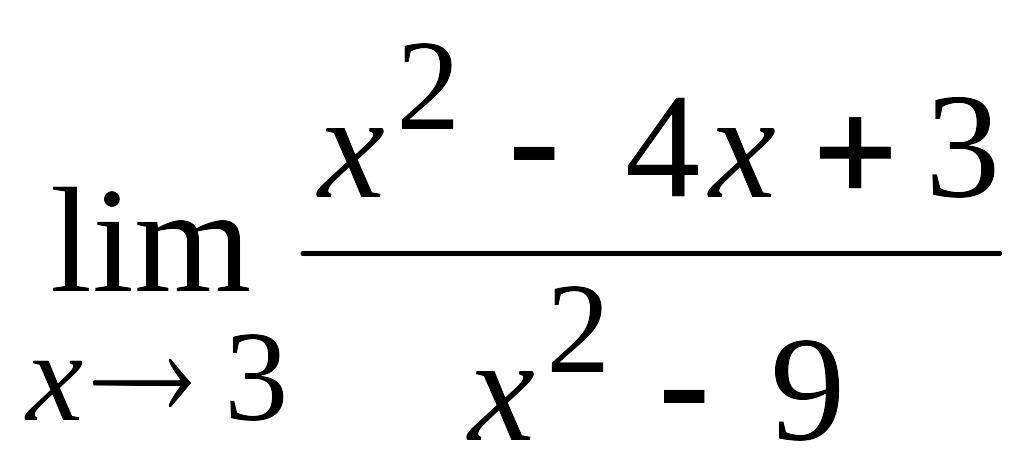ём . Имеем

.

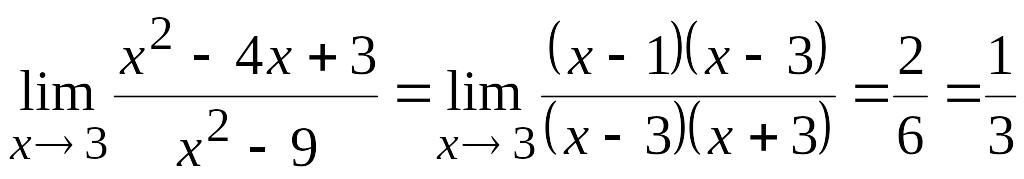Так как существует конечный предел в точке , означающий, что существуют оба односторонних предела, и они равны, но функция в этой точке не определена, то – точка устранимого разрыва.

Рассмотрим точку . Вычислим 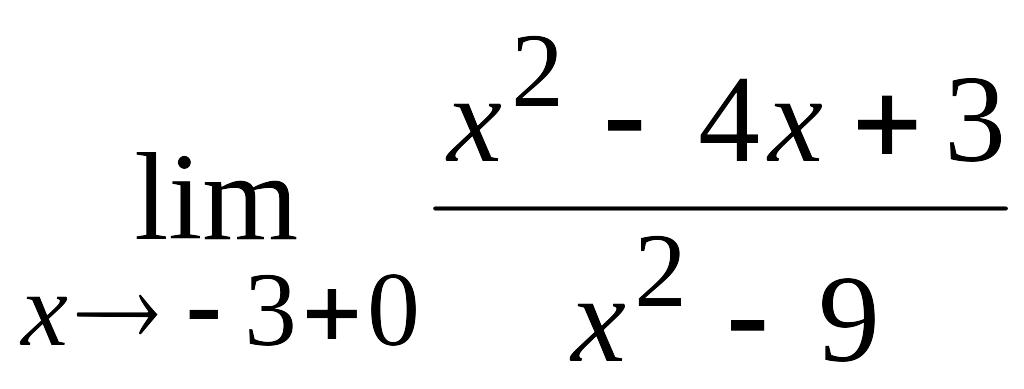. Так как при числитель дроби стремится к 24, а знаменатель является отрицательной бесконечно малой функцией, то ,

Далее, 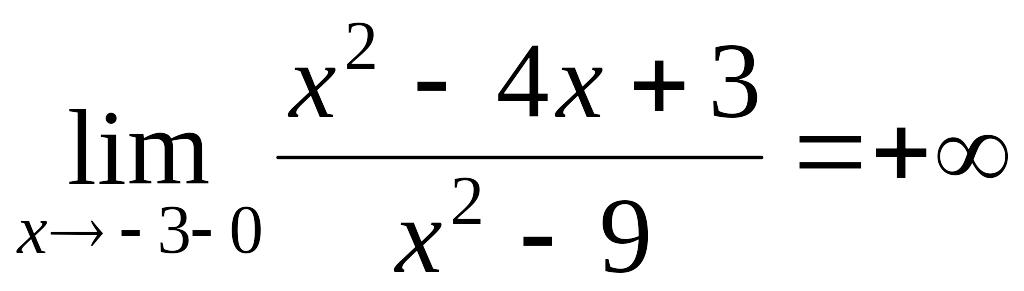, так как при числитель дроби стремится к 24, а знаменатель является положительной бесконечно малой функцией. Следовательно, односторонние пределы в точке бесконечны, и является точкой разрыва 2-го рода.

Пример 6.5. Найти точки разрыва функции 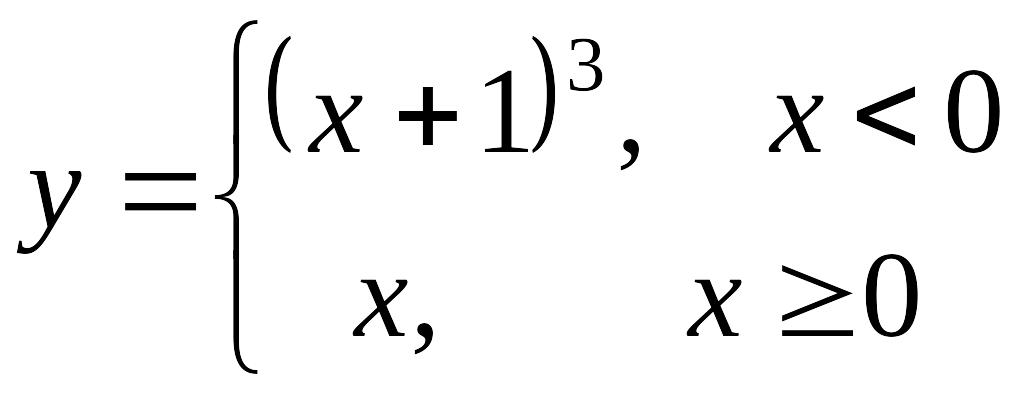и определить их характер.

При функция является непрерывной, как элементарная. При функция – тоже непрерывная функция, как элементарная.

Исследуем поведение функции в точке , для чего вычислим односторонние пределы в этой точке.

; .

Так как односторонние пределы конечны и , то – точка разрыва 1-го рода. Построим график заданной функции.

Пример 6.6. Исследовать функцию на непрерывность и построить её график

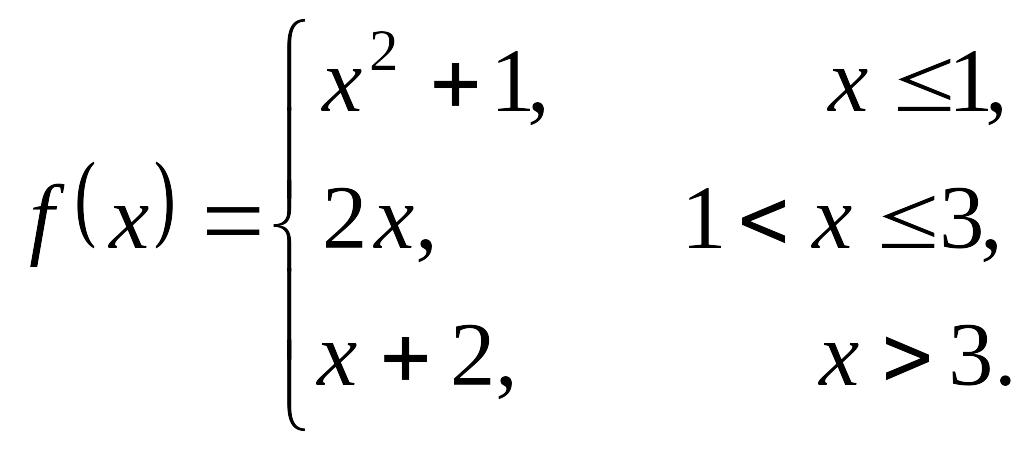
Заданная функция является непрерывной во всех точках, за исключением, быть может, тех точек, в которых меняется аналитическое выражение, то есть, при и . Рассмотрим односторонние пределы в точке .

;

Вычислим значение функции в точке :

.

Так как , то является точкой непрерывности функции.

Рассмотрим односторонние пределы в точке .

; .

Так как в точке существуют конечные односторонние пределы, не равные друг другу, то – точка разрыва 1-го рода.

Построим график функции