
- •1. Вычисление пределов на бесконечности.
- •2. Вычисление пределов от рациональной функции в конечной точке.
- •3. Вычисление пределов, содержащих иррациональность.
- •4. Первый замечательный предел.
- •5. Второй замечательный предел.
- •6. Точки разрыва функции.
- •Производная функции.
- •10. Промежутки монотонности функции.
- •11. Экстремумы функции.
- •Так как то горизонтальных асимптот нет.
- •14. Исследование функции и построение ее графика.
- •Решение. По формуле (1) имеем
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего
профессионального образования
«Южно-Российский государственный университет экономики и сервиса»
(ФГБОУ ВПО «ЮРГУЭС»)
УТВЕРЖДАЮ
Заведующий кафедрой
«Математика»
И.М.Мальцев
«03» сентября 2012 г.
На правах рукописи
КУРС ЛЕКЦИЙ
«МАТЕМАТИКА (модуль 2)»
для студентов 1-го курса
Учебно-методическое пособие к самостоятельному изучению
отдельных разделов дисциплины «Математика»
Электронный образовательный ресурс
(Для студентов всех форм обучения)
Авторы (составители):
к.т.н., доцент О.А. Алейникова
Рассмотрен и рекомендован
для использования в учебном процессе на 2012/2013 – 2017/2018 уч. г. на заседании Кафедры «Математика». Протокол № 1 от 03 09 2012 г.
Шахты 2012
Определения и понятия, которые известны из школьного курса.
1. Множество – совокупность некоторых объектов, объединённых по какому-нибудь признаку. Его объекты – элементы. Множество, не содержащее ни одного элемента, - пустое (обозначается Ø). Числовые множества:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
А - подмножество В.
,
А - подмножество В.
![]() - сложение.
- сложение.
![]() - умножение.
- умножение.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
I – множество иррациональных
чисел, десятичных непериодических
дробей.
,
I – множество иррациональных
чисел, десятичных непериодических
дробей.
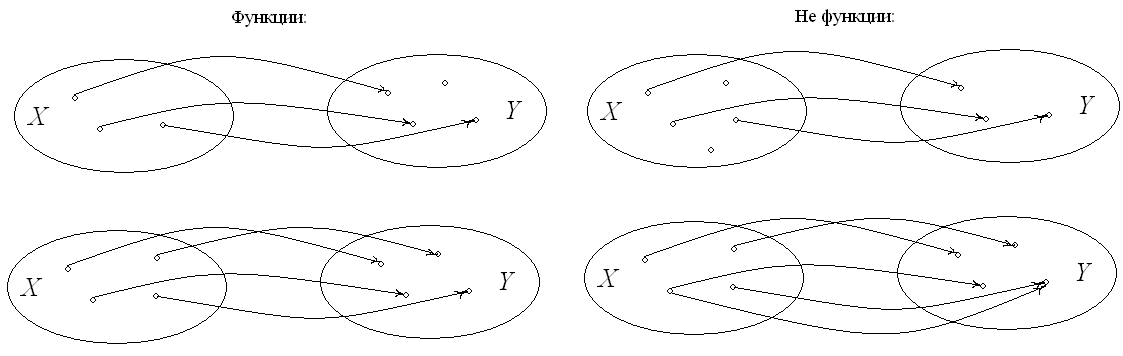
2. Соответствие
(правило) f, которое каждому
элементу
![]() сопоставляет один и только один элемент
сопоставляет один и только один элемент
![]() ,
называется функцией, действующий
из Х в У.
,
называется функцией, действующий
из Х в У.
![]() .
Или
.
Или
![]() .
Х – область определения
.
Х – область определения
![]() .
У – область значений
.
У – область значений
![]() .
Если
.
Если
![]() и
и
![]() ,
это числовая функция. х – аргумент.
у – функция. Задать функцию - задать
правило. Три способа: аналитический,
графический и табличный.
,
это числовая функция. х – аргумент.
у – функция. Задать функцию - задать
правило. Три способа: аналитический,
графический и табличный.
3. Если
![]() - чётная. Если
- чётная. Если
![]() - нечётная.
- нечётная.
4. Если для любых
![]() из того, что
из того, что
![]()
![]()
а)
![]() ,
то
- возрастающая на
,
то
- возрастающая на
![]() ;
;
б)
![]() ,
то
- не убывающая на
;
,
то
- не убывающая на
;
в)
![]() ,
то
- убывающая на
;
,
то
- убывающая на
;
г)
![]() ,
то
- не возрастающая на
;
,
то
- не возрастающая на
;
Такие функции называются монотонными на . В случаях а) и в) – строго монотонными.
5.
называется ограниченной на
,
если существует число М >0, что для всех
![]() выполняется
выполняется
![]() .
Т.е. график лежит между прямыми
.
Т.е. график лежит между прямыми
![]() и
и
![]() .
.
6.
называется периодической на
,
если существует число Т >0, что для всех
![]() и
и
![]() .
Т – период. Основной период – наименьший.
.
Т – период. Основной период – наименьший.
7. Если функция
взаимнооднозначная, т.е. если каждому
![]() соответствует единственный
,
то определена
соответствует единственный
,
то определена
![]() с областью определения Е и множеством
значений -
.
Такая функция называется обратной
к
.
с областью определения Е и множеством
значений -
.
Такая функция называется обратной
к
.
![]() .
.
и
- взаимно обратные. Графики взаимно
обратных функций симметричны относительно
прямой
![]() .
.
Примеры.
8. Пусть
![]() определена на
,
а
определена на
,
а
![]() ,
,
![]() ,
причём, каждому
соответствующее значение
,
причём, каждому
соответствующее значение
![]() .
Тогда на
.
Тогда на
![]() определена функция
определена функция
![]() ,
которая называется сложной функцией
от
,
которая называется сложной функцией
от
![]() (
суперпозицией или функцией от функции).
(
суперпозицией или функцией от функции).
![]() - промежуточный аргумент. Сложная функция
может иметь несколько промежуточных
аргументов.
- промежуточный аргумент. Сложная функция
может иметь несколько промежуточных
аргументов.
9.
![]() - точка максимума (минимума)
функции
,
если найдётся для неё
- точка максимума (минимума)
функции
,
если найдётся для неё
![]() - окрестность: для любого
:
- окрестность: для любого
:
![]()
![]() (
(![]() ).
Это точки экстремума. Это не всегда
наибольшее и наименьшее значения
функции.
).
Это точки экстремума. Это не всегда
наибольшее и наименьшее значения
функции.
Основные элементарные функции.
1. Показательная:
![]() .
.
2. Степенная:
![]() (
,
(
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
3. Логарифмическая:
![]() .
.
4. Тригонометрические:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
5 Обратные
тригонометрические:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных, с помощью конечного числа арифметических действий и операций «функции от функции», называется элементарной функцией.
Теоремы о непрерывных функциях.
1. Всякая элементарная функция непрерывна в своей естественной области определения.
1). Многочлен
![]() непрерывен
на
непрерывен
на
![]() .
.
2). Рациональная
функция
 непрерывна во всех точках
кроме нулей
непрерывна во всех точках
кроме нулей
![]() .
.
3). Функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() непрерывны
на
.
непрерывны
на
.
4). Функция
![]() непрерывна при
непрерывна при
![]() .
.
5). Функция
![]() непрерывна при
непрерывна при
![]() .
.
6). Функции
![]() ,
,
![]() непрерывны на
непрерывны на
![]() .
.
7). Функции
![]() ,
,
![]() непрерывны при
непрерывны при
![]() .
.
Пример. Рассмотрим
функцию
![]() .
Она непрерывна в точке
.
Она непрерывна в точке
![]() ,
поэтому
,
поэтому
![]()
![]()
![]() .
.
2. (Вейерштрасса) Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Следствие: Если функция непрерывна на отрезке, то она ограничена на нём.
3. (Больцано-Коши)
Если функция непрерывна на отрезке и
принимает на его концах неравные значения
![]() и
и![]() ,
то на нём она принимает и все промежуточные
значения между А и В.
,
то на нём она принимает и все промежуточные
значения между А и В.
Следствие: Если функция непрерывна на отрезке и принимает на его концах значения разных знаков, то внутри отрезка найдётся хотя бы одна точка, в которой данная функция обращается в нуль.
Определение.
![]() – окрестностью (в дальнейшем просто
окрестностью) точки
– окрестностью (в дальнейшем просто
окрестностью) точки
![]() называется интервал
называется интервал
![]() ,
,
![]() .
.
Проколотая
окрестность точки
![]() – множество
– множество
![]() \
\![]() .
.
Окрестность символа
![]() :
:
![]() .
.
Окрестность символа
![]() :
:
![]() .
.
Окрестность символа
![]() :
:
![]() .
.
Определение.
Точка
![]() (или бесконечный символ) называется
точкой сгущения множества
(или бесконечный символ) называется
точкой сгущения множества
![]() ,
если любая окрестность точки
содержит точки множества
,
отличные от
.
,
если любая окрестность точки
содержит точки множества
,
отличные от
.
Пусть функция
![]() и
–
точка сгущения множества
.
и
–
точка сгущения множества
.
Определение.
Число (или бесконечный символ) А
называется пределом функции
![]() при
при
![]() ,
если для любой окрестности
,
если для любой окрестности
![]() точки А найдётся проколотая
окрестность
точки А найдётся проколотая
окрестность
![]() точки
такая,
что
точки
такая,
что
![]() для любого
для любого
![]() .
.
Обозначение:
![]() .
.
Если в определении
предела функции в конечной точке а
потребовать дополнительное условие
![]() ,
то получим определение предела справа
(слева).
,
то получим определение предела справа
(слева).
Обозначения:![]() ,
,
![]() – предел справа,
– предел справа,
![]() ,
,
![]() – предел слева.
– предел слева.
Графически
![]() можно изобразить, например, следующим
образом:
можно изобразить, например, следующим
образом:

Одним из примеров
числовой функции может служить числовая
последовательность
![]() (
(![]() ).
).
Определение предела последовательности можно дать следующим образом:
Число (или
бесконечный символ) А называется
пределом числовой последовательности
,
если для любой окрестности
найдётся такой номер
![]() ,
что
,
что
![]() для всех
для всех
![]() .
.
Пример. Рассмотрим
последовательность
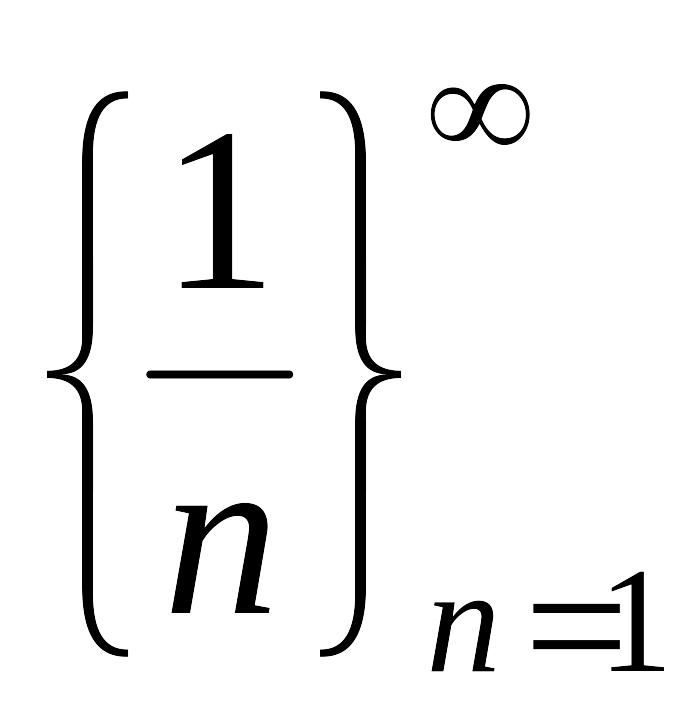 и покажем, что
и покажем, что
![]() .
Возьмём произвольную окрестность
.
Возьмём произвольную окрестность
![]() точки 0 и номер
точки 0 и номер
![]() .
Тогда при всех
.
Тогда при всех
![]() будет справедливо неравенство
будет справедливо неравенство
![]() ,
т.е.
,
т.е.
![]() при всех
.
Таким образом,
.
при всех
.
Таким образом,
.
Определение.
Функция
![]() называется бесконечно малой (б.м.) при
,
если
называется бесконечно малой (б.м.) при
,
если
![]() .
.
Определение.
Функция
называется бесконечно большой (б.б.) при
,
если функция
 является б.м. при
.
является б.м. при
.
Для бесконечно
большой функции
![]() .
.
Пример. Функция
![]()
![]() при
при
![]() является б. б., т.к. функция
является б. б., т.к. функция
![]() – б.м. при
.
– б.м. при
.
Отметим некоторые основные свойства пределов функции.
1. Если существует предел функции в точке а, то он единственен.
2. Для того чтобы в точке а существовал предел функции , необходимо и достаточно, чтобы в этой точке у функции существовали равные односторонние пределы справа и слева.
3. Если существуют
конечные пределы
,
![]() ,
то
,
то
а)
![]() ;
;
б)
![]() ,
,
![]()
![]() ;
;
в)
![]() ;
;
г)
 ,
,
![]() .
.
4. Для того, чтобы
функция
имела конечный предел равный А при
,
необходимо и достаточно, чтобы в некоторой
проколотой окрестности точки а
имело место представление
![]() ,
где
,
где
![]() – б.м. при
.
– б.м. при
.
5. Если
![]() –
б.м. функция при
,
– ограниченная функция в некоторой
проколотой окрестности точки а, то
–
б.м. функция при
,
– ограниченная функция в некоторой
проколотой окрестности точки а, то
![]() – б.м. при
.
– б.м. при
.
6. Если в некоторой
проколотой окрестности точки а
выполнено неравенство
![]() и существуют пределы функций
,
и существуют пределы функций
,
![]() при
,
то
при
,
то
![]() .
.
Пример. Пусть
![]() –
многочлен степени
–
многочлен степени
![]() .
Найдем
.
Найдем
![]() .
Имеем
.
Имеем
![]()
![]()
Так как
![]() и
и
![]() ,
,
то
![]() .
Следовательно, любой многочлен степени
не ниже 1 является бесконечно большой
функцией на бесконечности. Отсюда, в
частности, следует, что
.
Следовательно, любой многочлен степени
не ниже 1 является бесконечно большой
функцией на бесконечности. Отсюда, в
частности, следует, что
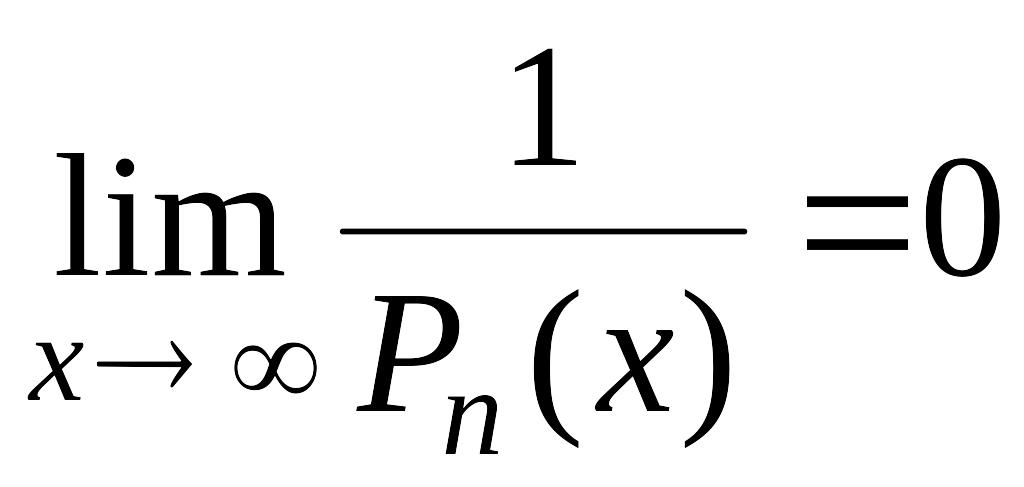 .
.
Определение.
Функция
называется непрерывной в точке
![]() ,
если
,
если
![]() .
.
Таким образом, чтобы найти предел непрерывной функции в точке , нужно вычислить значение функции в этой точке.
Если
![]()
![]() ,
то функция
называется непрерывной справа (слева)
в точке
.
,
то функция
называется непрерывной справа (слева)
в точке
.
Отметим некоторые свойства непрерывных функций.
1) Для того чтобы функция была непрерывной в точке , необходимо и достаточно, чтобы она была непрерывна справа и слева в этой точке.
2) Если функции
и
непрерывны в точке
,
то функции
+
,
,
/
(![]() )
непрерывны в точке
.
)
непрерывны в точке
.
3) Если функция
непрерывна в точке
,
а функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
то сложная функция
,
то сложная функция
![]() непрерывна в точке
.
непрерывна в точке
.
Определение. Функция называется непрерывной на множестве , если она непрерывна в каждой точке этого множества.
Основные элементарные функции непрерывны в своей естественной области определения:
1). Многочлен
![]() непрерывен на
непрерывен на
![]() .
.
2). Рациональная
функция
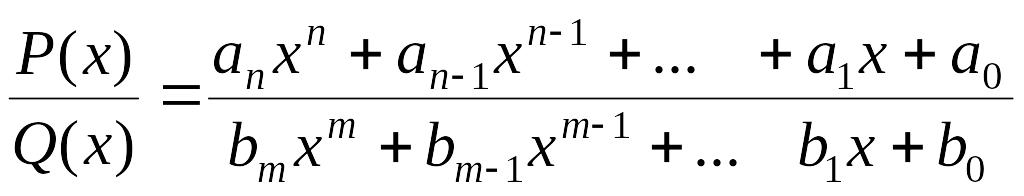 непрерывна во всех точках
кроме нулей
непрерывна во всех точках
кроме нулей
![]() .
.
3). Функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() непрерывны на
.
непрерывны на
.
4). Функция
![]() непрерывна при
непрерывна при
![]() .
.
5). Функция
![]() непрерывна при
непрерывна при
![]() .
.
6). Функции
![]() ,
,
![]() непрерывны на отрезке
непрерывны на отрезке
![]() .
.
7). Функции
![]() ,
непрерывны при
,
непрерывны при
![]() .
.
Пример.
Рассмотрим функцию
![]() .
Она непрерывна в точке
.
Она непрерывна в точке
![]() ,
поэтому
,
поэтому
![]()
![]() .
.
Определение. Пусть функция определена в некоторой окрестности точки , кроме, быть может, самой этой точки. Точка называется точкой разрыва функции , если функция не определена в точке или если она определена в этой точке, но не является в ней непрерывной.
Определение.
Точка
называется точкой устранимого разрыва
функции
,
если в этой точке существует конечный
предел
![]() ,
но в самой точке функция либо не
определена, либо значение функции в
точке
не совпадает со значением предела.
,
но в самой точке функция либо не
определена, либо значение функции в
точке
не совпадает со значением предела.
Определение.
Точка
называется точкой разрыва первого рода
функции
,
если в этой точке существуют конечные,
не равные между собой односторонние
пределы функции
.
Разность
![]() называется скачком функции в точке
.
называется скачком функции в точке
.
Точка разрыва, не являющаяся точкой устранимого разрыва и точкой разрыва первого рода, называется точкой разрыва второго рода.
Рассмотрим некоторые пределы, которые наиболее часто используются в дальнейшем.
Определение.
Предел
![]() называется первым замечательным
пределом.
называется первым замечательным
пределом.
С помощью этого предела нетрудно получить некоторые следствия:
![]() ;
;
![]() ;
;
![]() .
.
Определение.
Предел
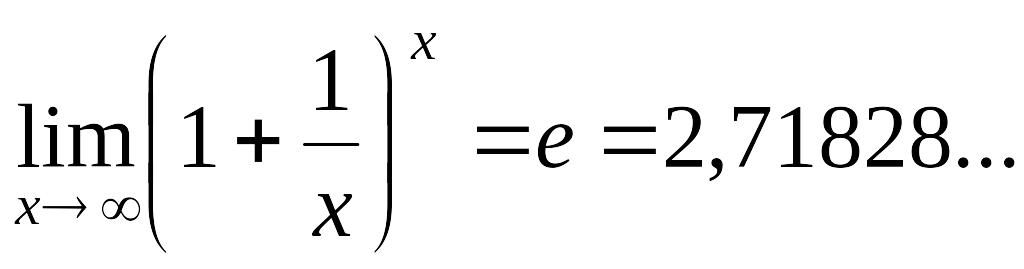 называется вторым замечательным
пределом.
называется вторым замечательным
пределом.
Используя этот предел, можно получить следующие результаты:
![]() ;
;
![]() ,
в частности,
,
в частности,
![]() ;
;
 ,
в частности,
,
в частности,
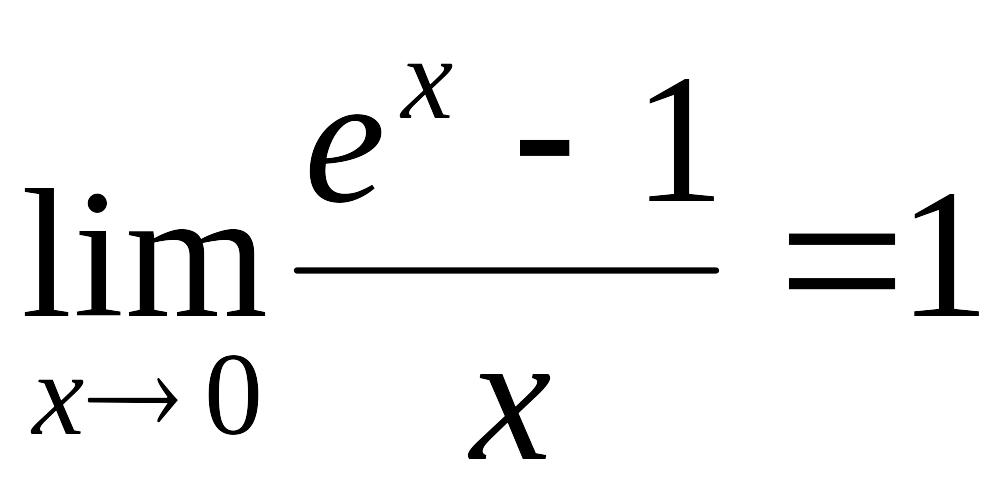 .
.
При вычислении пределов часто используется эквивалентность б.м. функций.
Определение.
Бесконечно малые функции
и
![]() при
называются эквивалентными, если
при
называются эквивалентными, если
 .
.
Обозначение ~ при .
Используя первый
и второй замечательные пределы и их
следствия, можно составить таблицу
эквивалентных бесконечно малых функций
при
![]() .
.
![]() ~
х
~
х
![]() х ~ х
х ~ х
~ х
![]() х ~ х
х ~ х
![]() ~ х
~ х
![]() ~ х
~ х
Пусть
![]() и
эквивалентные б.м. функции при
и существует предел
и
эквивалентные б.м. функции при
и существует предел
![]() .
Тогда существует
.
Тогда существует
![]() =
.
=
.
Иными словами, при вычислении пределов можно заменять бесконечно малый множитель на эквивалентную ему функцию.
ПРАКТИЧЕСКАЯ ЧАСТЬ
1. Вычисление пределов на бесконечности.
Пример 1.1 Найти
![]() .
.
![]() ,
так как
,
так как
![]() –
многочлен
–
многочлен
третьей степени
является б.б. функцией при
![]() .
.
Пример 1.2.
Вычислить
![]() .
.
Имеем
![]() ,
так как
,
так как
![]() –
б.б. функция при
.
–
б.б. функция при
.
Пример 1.3.
Вычислить
 .
.
 .
.
Пример 1.4.
Вычислить
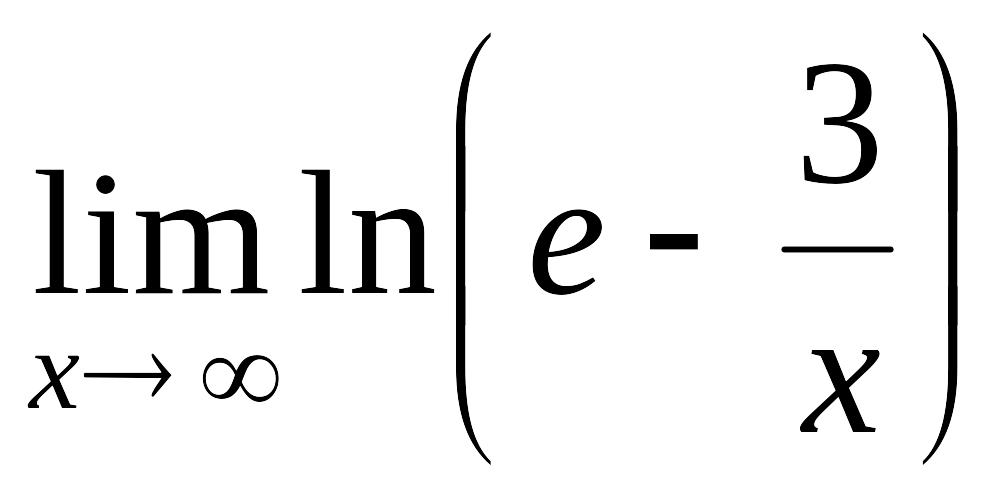 .
.
Так как
![]() –
непрерывная функция при
–
непрерывная функция при
![]() ,
то
,
то
 .
.
Пример 1.5.
Вычислить
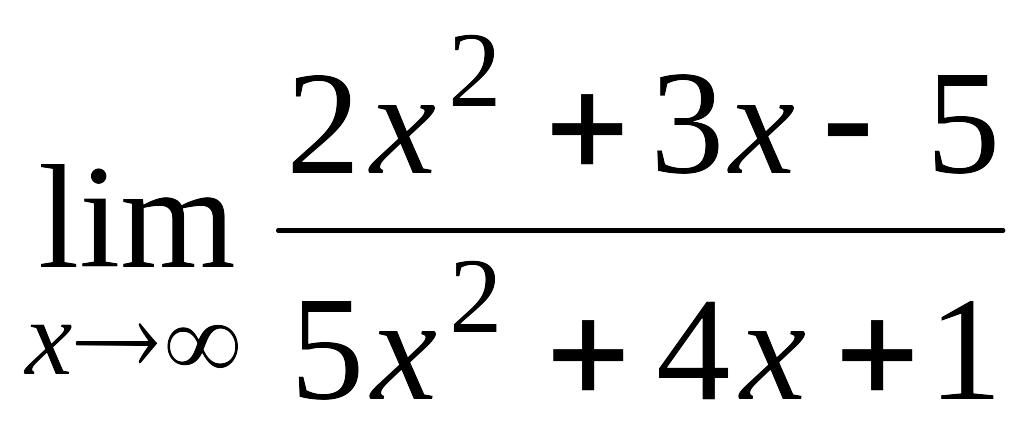 .
.
Числитель и
знаменатель дроби представляют собой
б. б. функции при
.
В этом случае говорят, что имеет место
неопределенность
![]() .
.

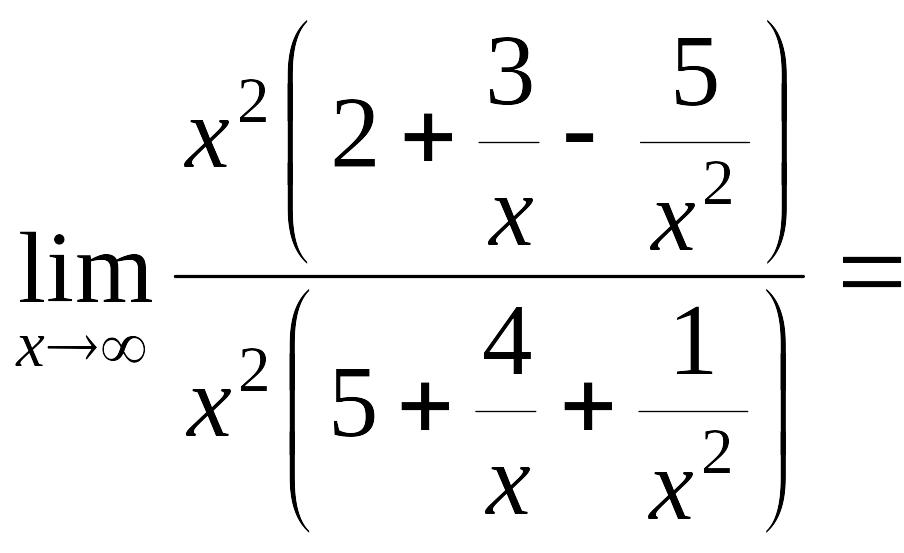
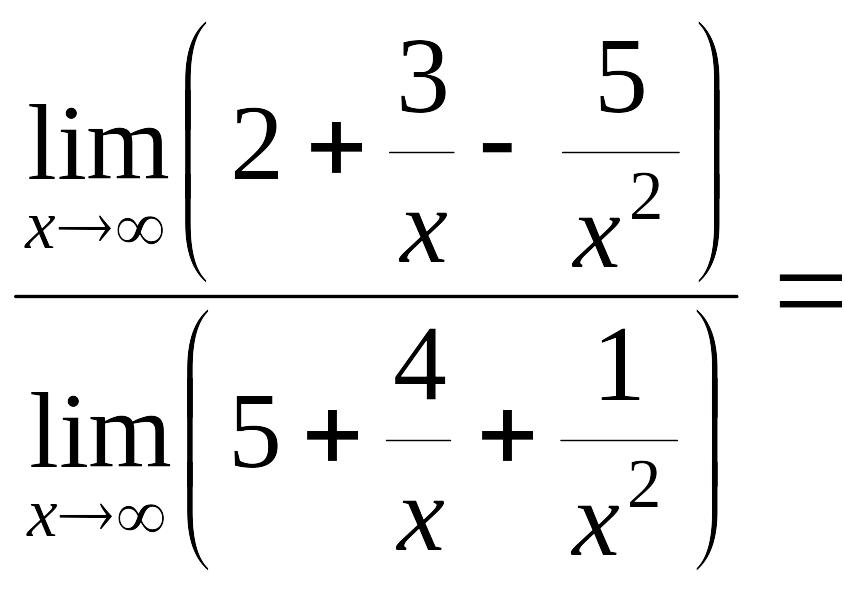
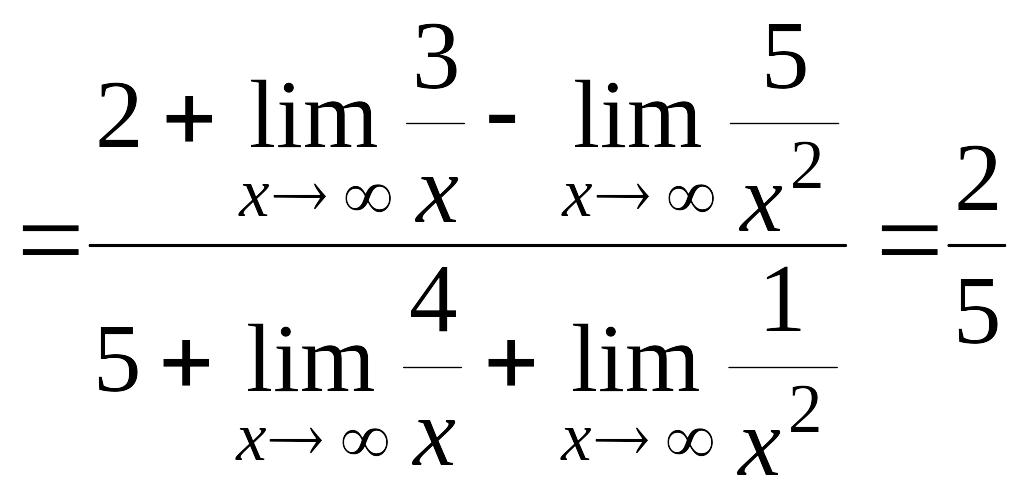 .
.
В дальнейшем не будем так подробно описывать применение свойств пределов.
Пример 1.6.
Вычислить
 .
.
Имеем

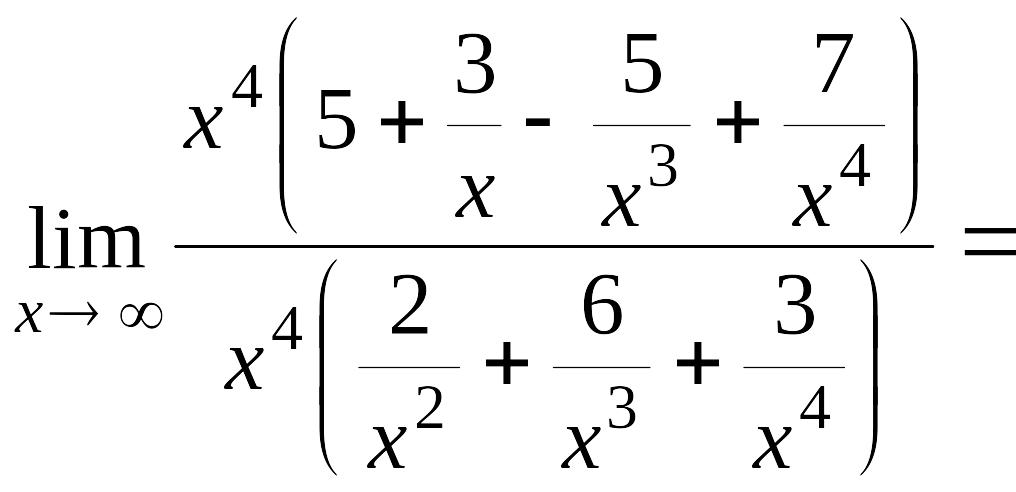
 ,
так как числитель дроби при
стремится к 5, а знаменатель является
б.м. функцией.
,
так как числитель дроби при
стремится к 5, а знаменатель является
б.м. функцией.
Пример 1.7.
Вычислить
![]() .
.
Разделим числитель
и знаменатель дроби на
![]() .
Получим
.
Получим
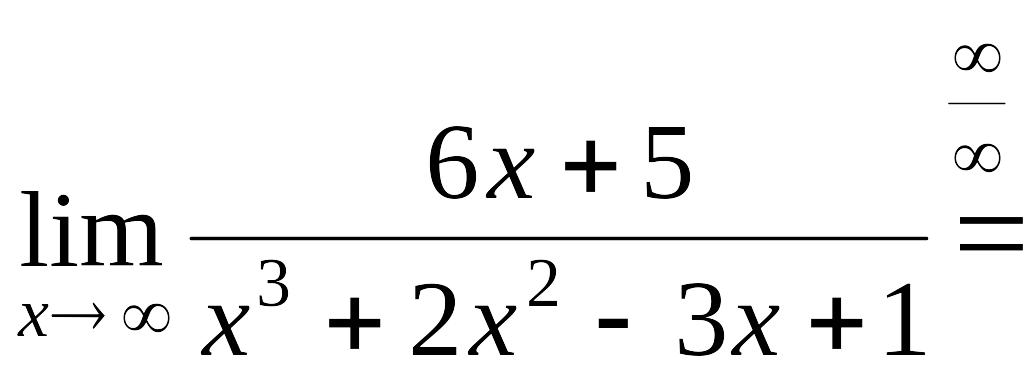
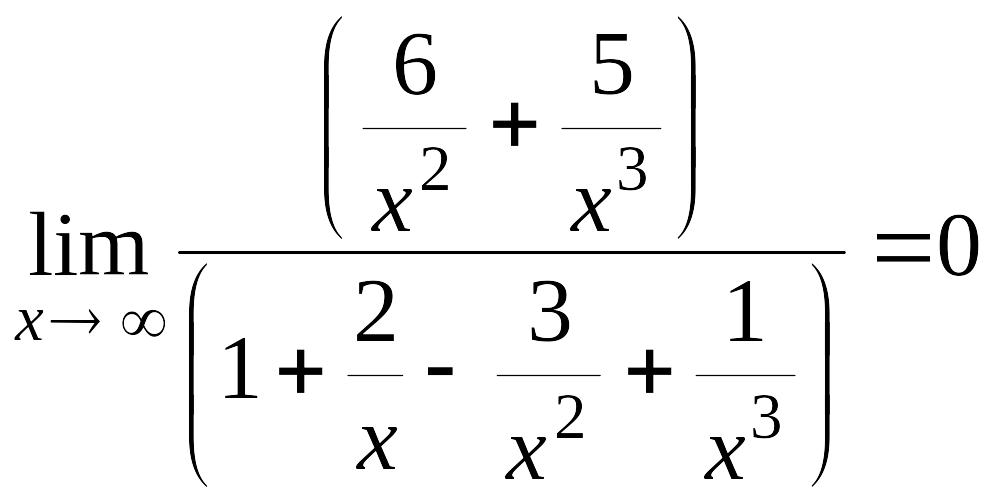 ,
так как числитель дроби при
стремится к 0, а знаменатель – к 1.
,
так как числитель дроби при
стремится к 0, а знаменатель – к 1.
Проанализируем
решение последних трёх примеров. Все
они представляют собой предел отношения
многочленов при
.
В первом случае имело место равенство
степеней многочленов числителя и
знаменателя. Предел в этом случае равен
отношению коэффициентов при старших
степенях
![]() .
Во втором примере в числителе – многочлен
4-ой степени, а в знаменателе – 2-ой
степени. Предел отношения многочленов
равен
.
Наконец, в 3-м примере в числителе стоит
многочлен 1-ой степени, в знаменателе –
3-ей. Предел равен 0.
.
Во втором примере в числителе – многочлен
4-ой степени, а в знаменателе – 2-ой
степени. Предел отношения многочленов
равен
.
Наконец, в 3-м примере в числителе стоит
многочлен 1-ой степени, в знаменателе –
3-ей. Предел равен 0.
В общем случае имеет место правило: если
![]() ,
,
![]() ,
,
то
 .
.
В дальнейшем можно пользоваться этим правилом при вычислении подобных примеров.
Пример 1.8.
![]() ,
так как
,
так как
![]() .
.
Пример 1.9.
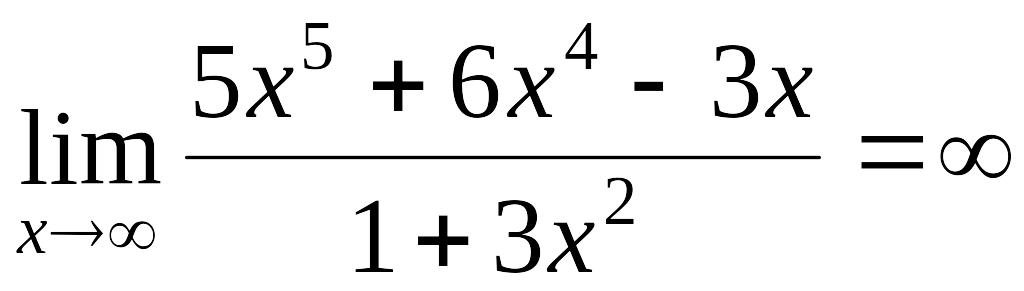 ,
так как
,
так как
![]() .
.
Пример 1.10.
 ,
так как
,
так как
![]() .
.
Пример 1.11.

 ,
так как
,
так как
![]() .
.
Пример 1.12.

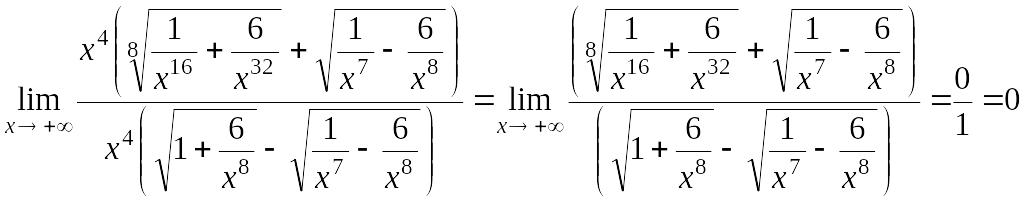 .
.
2. Вычисление пределов от рациональной функции в конечной точке.
Пример 2.1.
Вычислить
![]() .
.
Так как знаменатель
рациональной функции не обращается в
0 при
![]() ,
то эта функция непрерывна в точке
.
Значит
,
то эта функция непрерывна в точке
.
Значит
![]()
Пример 2.2.
Вычислить
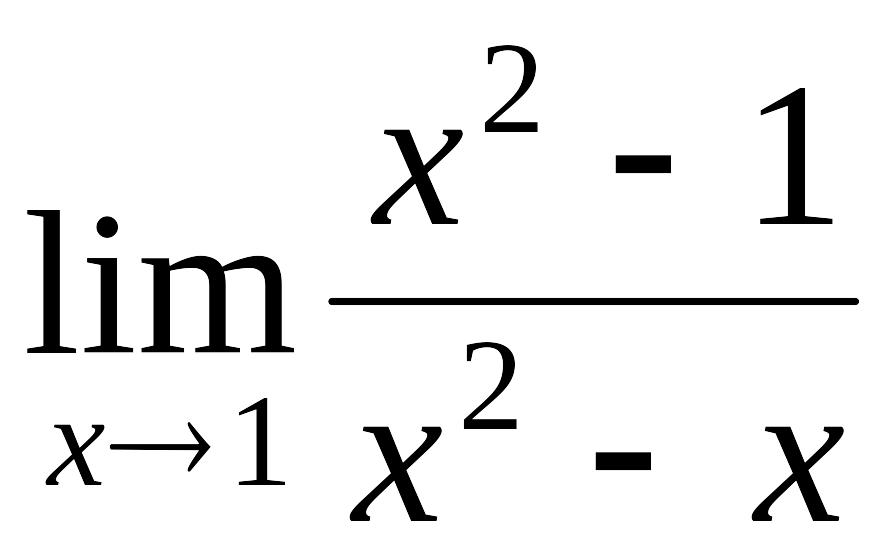 .
.
Числитель и
знаменатель дроби равны нулю при
.
В этом случае говорят, что имеет место
неопределённость вида
![]() .
В числителе разложим многочлен
.
В числителе разложим многочлен
![]() на множители по формуле
на множители по формуле
![]() ,
в знаменателе вынесем за скобку общий
множитель
.
Получим
,
в знаменателе вынесем за скобку общий
множитель
.
Получим
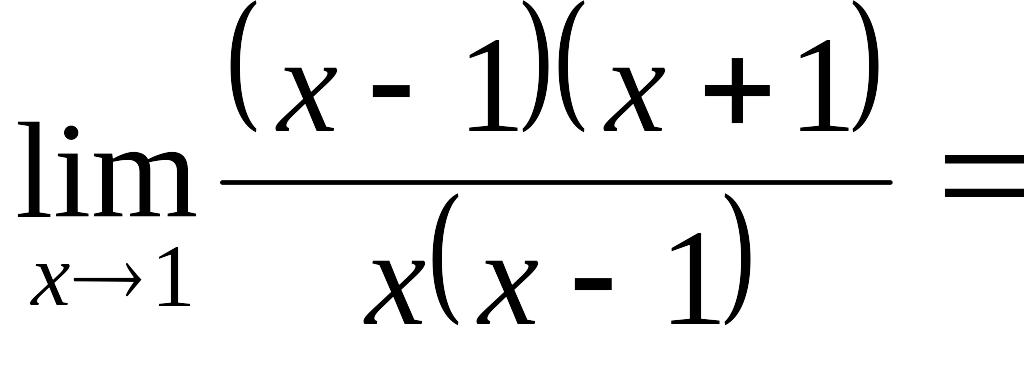
![]()
![]() .
.
Пример 2.3.
Вычислить
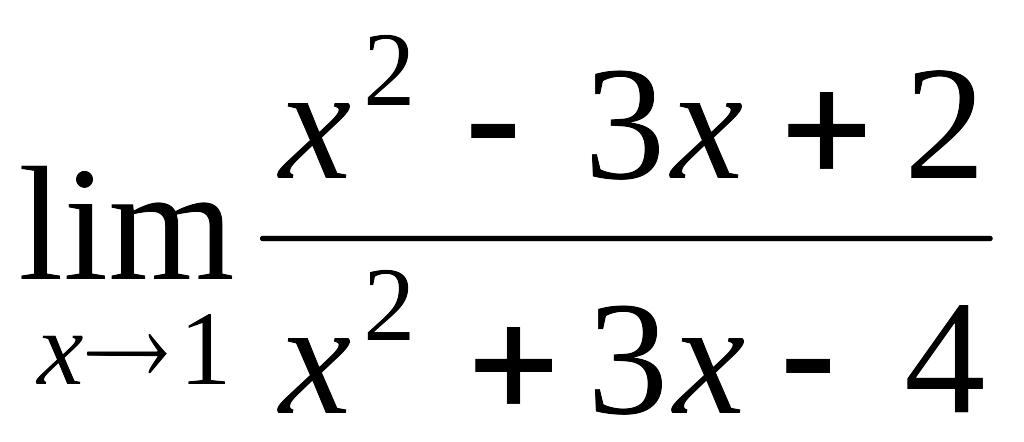 .
.
При подстановке
![]() в выражение
в выражение
 получаем неопределённость вида
получаем неопределённость вида
![]() .
Разложим многочлены
.
Разложим многочлены
![]() и
и
![]() на множители. Напомним, как в общем
случае можно найти корни квадратного
трёхчлена
на множители. Напомним, как в общем
случае можно найти корни квадратного
трёхчлена
![]() .
Вычислим дискриминант
.
Вычислим дискриминант![]() .
Если
.
Если
![]() ,
то корни находим по формулам:
,
то корни находим по формулам:
 .
Тогда
.
Тогда
![]() .
.
В нашем случае для трёхчлена
![]() ,
,
![]() ,
,
![]() .
.
Поэтому
![]() .
.
Таким же образом найдём корни квадратного трёхчлена .
![]() ,
,
![]() ,
,
![]() .
.
Тогда разложение
на множители имеет вид
![]() .
.
Итак,
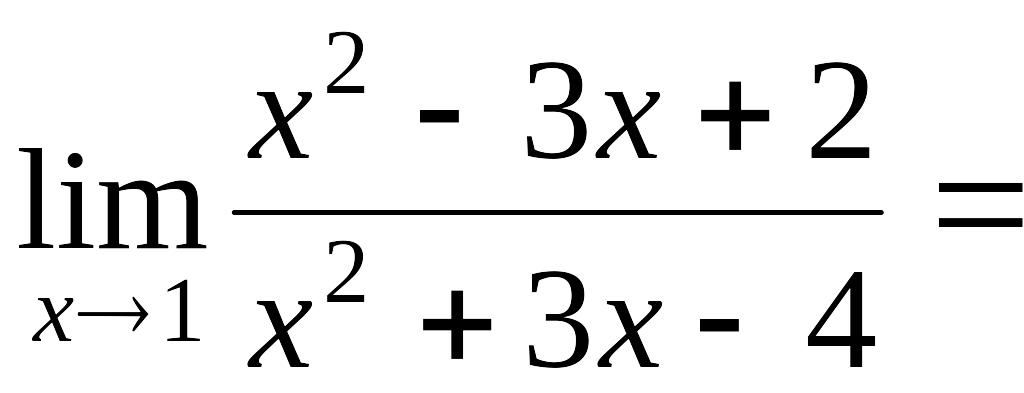
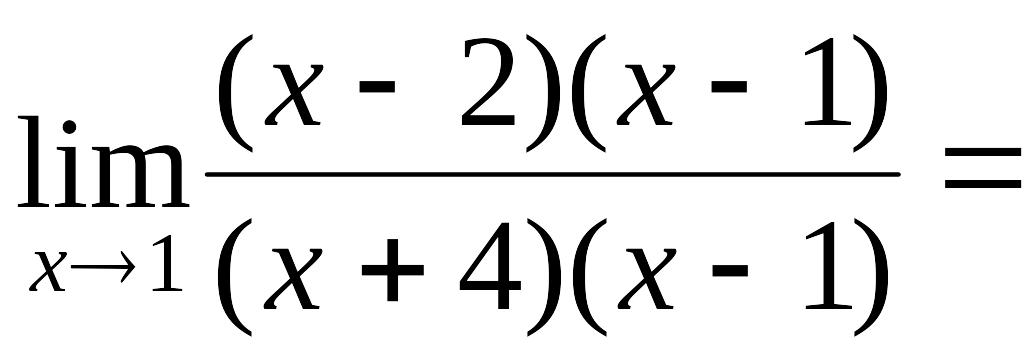
![]() .
.
Следующие два примера решаются подобным образом.
Пример 2.4.

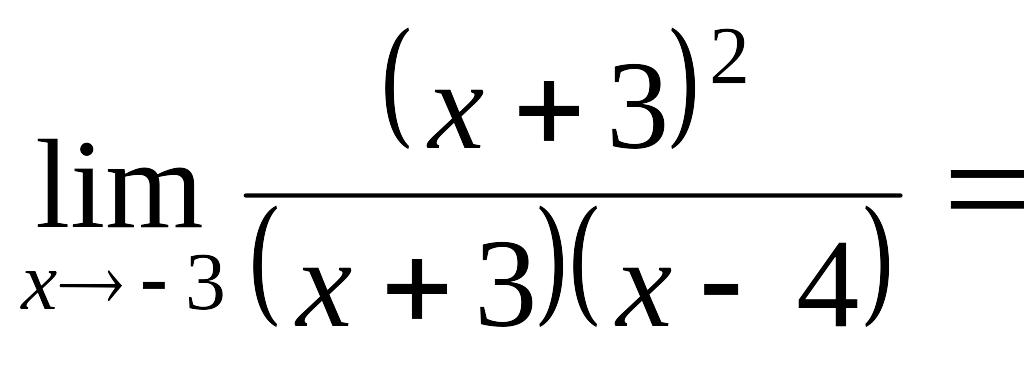
![]() .
.
Пример 2.5.
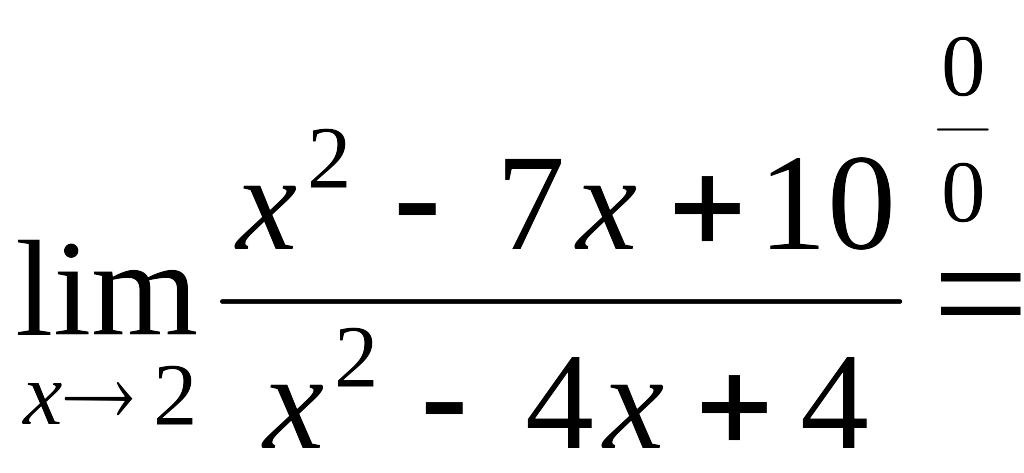
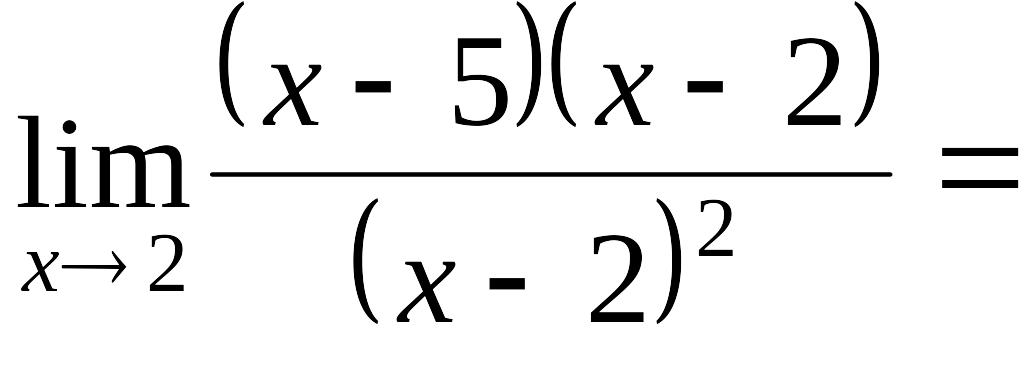
![]() .
.
Пример 2.6.
Вычислить
 .
.
Многочлен
![]() разложим на множители по формуле
разложим на множители по формуле
![]() .
.
Для многочлена
![]() найдём корни
найдём корни
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
=
 .
.
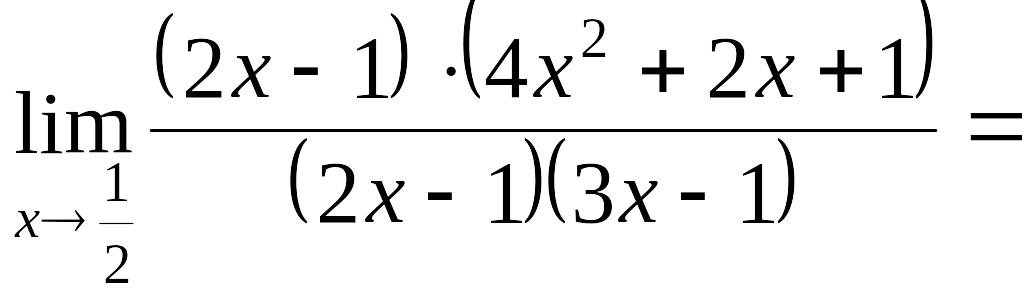
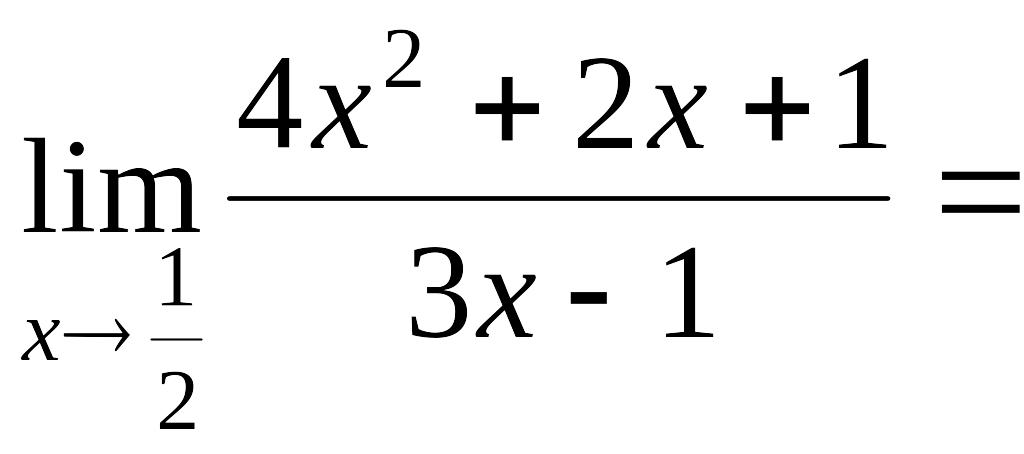
 .
.
Пример 2.7.
Вычислить
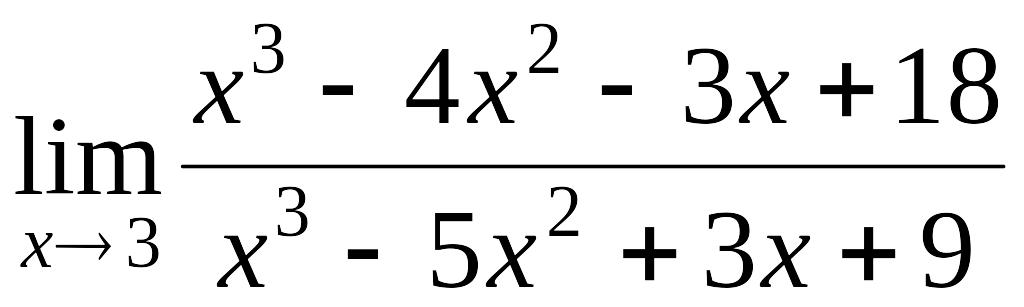 .
.
Имеет место
неопределённость вида
.
Так как
![]() является корнем многочленов
является корнем многочленов
![]() и
и
![]() ,
то каждый из них делится без остатка на
,
то каждый из них делится без остатка на
![]() .
.
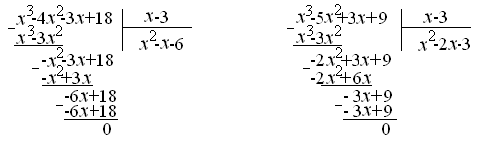
Получим

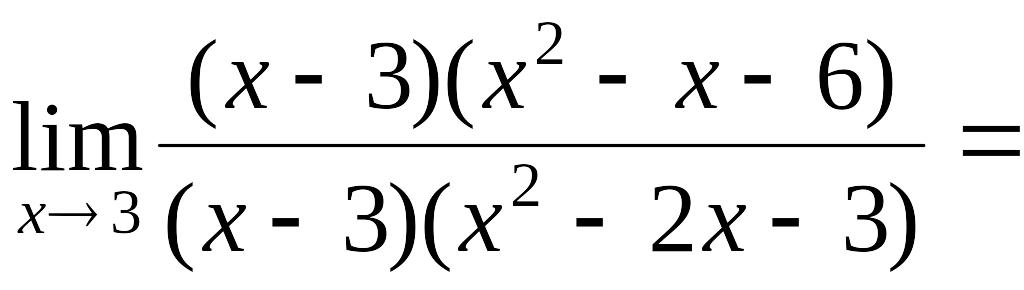
 ;
;
Так как неопределённость не исчезла, разложим на множители многочлены числителя и знаменателя.
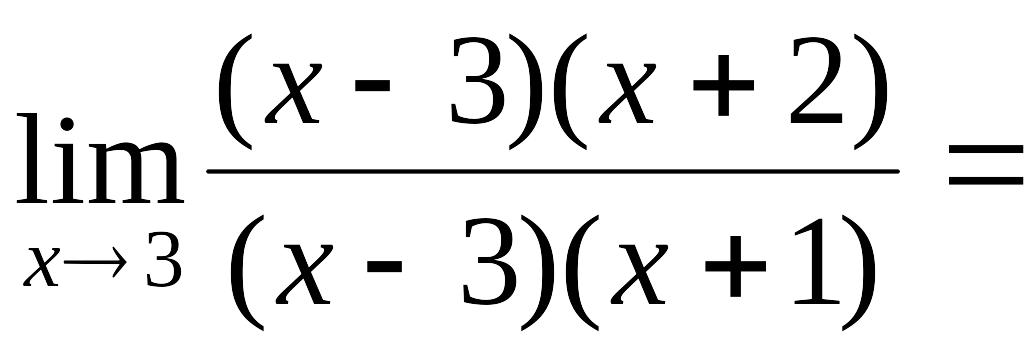
![]() .
.
