Лабораторная работа № 1
Определение плотности твердого тела
1. Цель работы
Развитие навыков работы с измерительными приборами (штангенциркулем, микрометром и техническими весами); формирование умений и навыков обработки результатов экспериментов в лабораторном практикуме.
1. Измерение длины и диаметра.
2. Взвешивание образца.
3. Определение плотности образца.
4. Расчет погрешности.
2. Теория вопроса
Штангенциркуль (рис. 1) измеряет длины не более 30 см с точностью 0,1 мм (0,05 мм):
Рис. 1.
Целые миллиметры отсчитывают по делениям линейки 1 штангенциркуля, а десятые доли миллиметра – по перемещающемуся нониусу 2, когда между ножками штангенциркуля зажат измеряемый предмет 3.
Нониусом называется дополнение к обычному масштабу (неподвижной линейки), позволяющее повысить плотность измерения с данным масштабом в 10-20 раз. Линейным нониусом называется маленькая линейка с делениями, которая может скользить вдоль большой линейки, называемой масштабом (рис. 1).
Деления
на нониусе наносятся обычно так, что
одно деление нониуса составляет
делений масштаба,
где
– число делений нониуса.
Именно
поэтому можно, пользуясь нониусом,
производить отсчеты с точностью до
части наименьшего деления масштаба.
В любом положении нониуса относительно масштаба одно из делений нониуса совпадает с каким-либо делением масштаба. Отсчет по нониусу основан на способности глаза фиксировать эти совпадения делений нониуса и масштаба. Если, а – цена деления штангенциркуля, b – цена деления масштабной линейки, m – число делений на нониусе, то связь между указательными делениями линейки и нониуса следующая:
am = (m - 1) b. (1)
Получаемая из формулы (1) разность
b - a = b / m (2)
называется точностью нониуса.
Искомая длина тела 3 определяется по формуле
L = kb + nb/m. (3)
Если положить, что b = 1 мм, m = 10 делений, то искомая длина
L = (k + n/10) мм, (4)
где k – целое число стальной миллиметровой линейки 1 (см. рис. 1) в мм, укладывающейся в измеряемой длине; n – число, показывает тот номер деления нониуса, который совпадает с некоторым делением линейки 1. Например, k = 14 мм, n = 5.
L = (14 + 5/10)= 14. 5 мм. (5)
Микрометр (рис. 2) позволяет измерять длину (диаметр) не более 25 мм с точностью 0,01 мм. Он состоит из 2-х основных частей: скобы 1 и микрометрического винта 4. Винт скреплен с барабаном 5, имеющим деления по окружности. Поворот барабана на одно деление приводит к смещению винта на 0,01 мм.
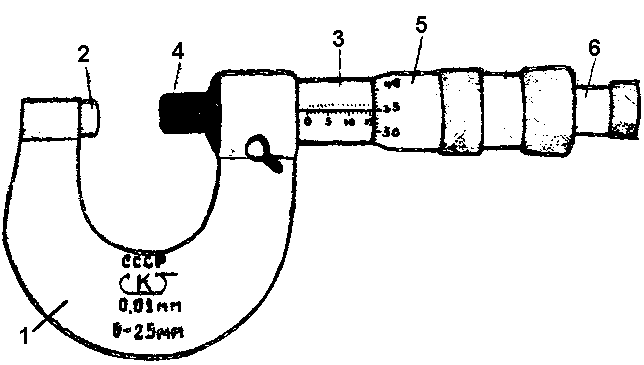
Рис.2
На стержне винта 4 укреплен барабан 6 с нанесенной на нем шкалой, имеющей 50 или 25 делений. При зажатом винте нуль барабана стоит против нуля линейной шкалы 3.
Целые миллиметры отсчитывают по неподвижной шкале на стебле 3, а сотые доли миллиметра – по делениям шкалы на барабане 5.
Для измерения микрометром предмет помещают между упором 2 и микрометрическим винтом 4, который осторожно подводят до соприкосновения при помощи “трещотки” 6, обеспечивающей постоянство нажима.
Главным источником ошибок является неравномерность нажатия винта на измеряемый предмет. Для устранения этого недостатка современные микрометры снабжаются специальным приспособлением, не допускающим слишком сильного нажатия. Момент нажатия фиксируется слабым щелчком. После этого «трещотка» 6 прокручивается с характерным треском, при этом барабан нельзя трогать.
Числовое значение D(L) измеряемого предмета (в данной работе измеряют диаметр цилиндра и толщину пластинки) находят по формуле
D = kb + n b/m, (6)
где k – число наименьших делений шкалы, b – цена наименьшего деления шкалы, m – число всех делений на шкале барабана, n – номер того деления барабана, которое в момент отсчета совпадает с осью шкалы стебля 4.
В данной работе применяется микрометр, у которого b=0,5 мм, m=50, и формула (6) примет вид
D = (0,5 k + n/100), мм (7)
На рис. 2 отсчет по микрометру показывает:
D = (0,5 30 + 35/100) = 15,35 мм.
Плотность однородного тела равна отношению массы этого тела к его объему:
= m / V. (8)
В данной работе массу измеряют с помощью технических весов, а объем тела правильной геометрической формы вычисляют по линейным размерам, полученным с помощью штангенциркуля и микрометра.