1.6. Относительный покой жидкости
Относительным покоем жидкости называется случай её движения, при котором вся масса жидкости движется как твердое тело, отдельные её части не смещаются одна относительно другой.
Рассмотрим два случая.
Случай первый. Сосуд с жидкостью движется прямолинейно и равноускоренно (рис. 1.13).
Пусть
сосуд движется с ускорением a.
Сила инерции
направлена в сторону, обратную ускорению,
сила тяжести
направлена вниз. Найдем направление и
величину равнодействующей массовой
силы:
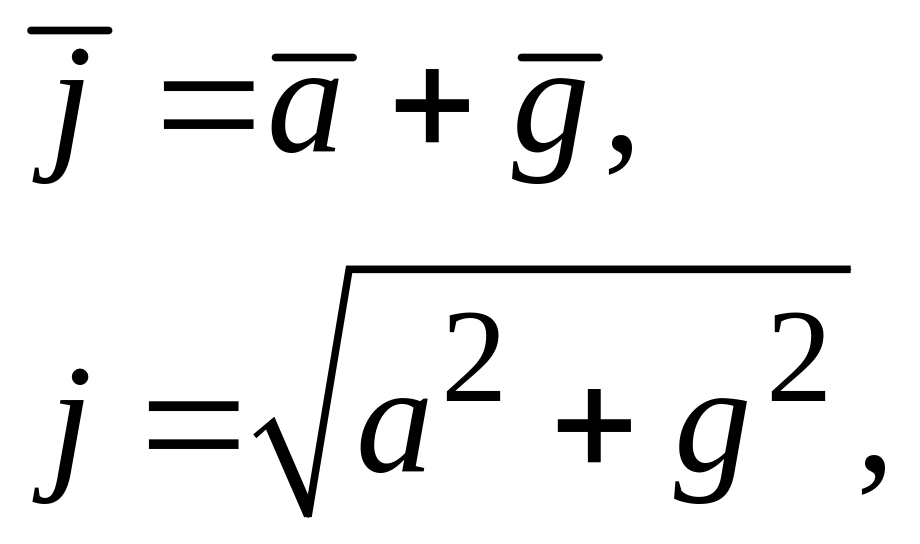(1.30)
где
и
– векторы единичных сил инерции и
тяжести. Для всех частиц рассматриваемого
объема жидкости равнодействующие
массовые силы параллельны друг другу,
а поверхности уровня перпендикулярны
к этим силам, в том числе и свободная
поверхность.
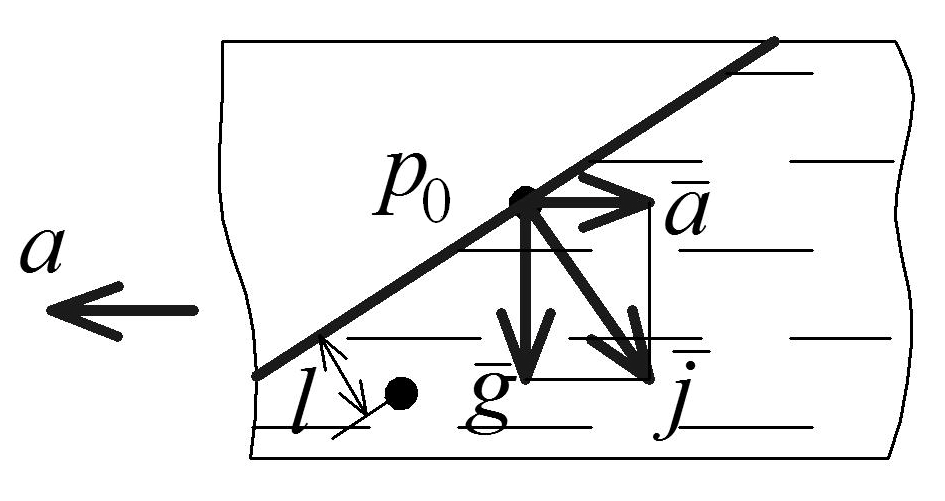
Рис. 1.13. Схема относительного покоя жидкости
Давление в любой точке определяется по формуле:
(1.31)
где
– давление на свободной поверхности,
j
– единичная массовая сила,
– плотность жидкости, l
– расстояние по нормали от точки до
свободной поверхности. Если
,
то
,
и уравнение (1.31) превратится
в основное
уравнение гидростатики.
Случай
второй. Сосуд
равномерно вращается вокруг вертикальной
оси с угловой скоростью
(рис. 1.14).
В данном случае массовыми силами являются сила тяжести и центробежная сила.
Воспользуемся основным дифференциальным уравнением гидростатики (1.3):
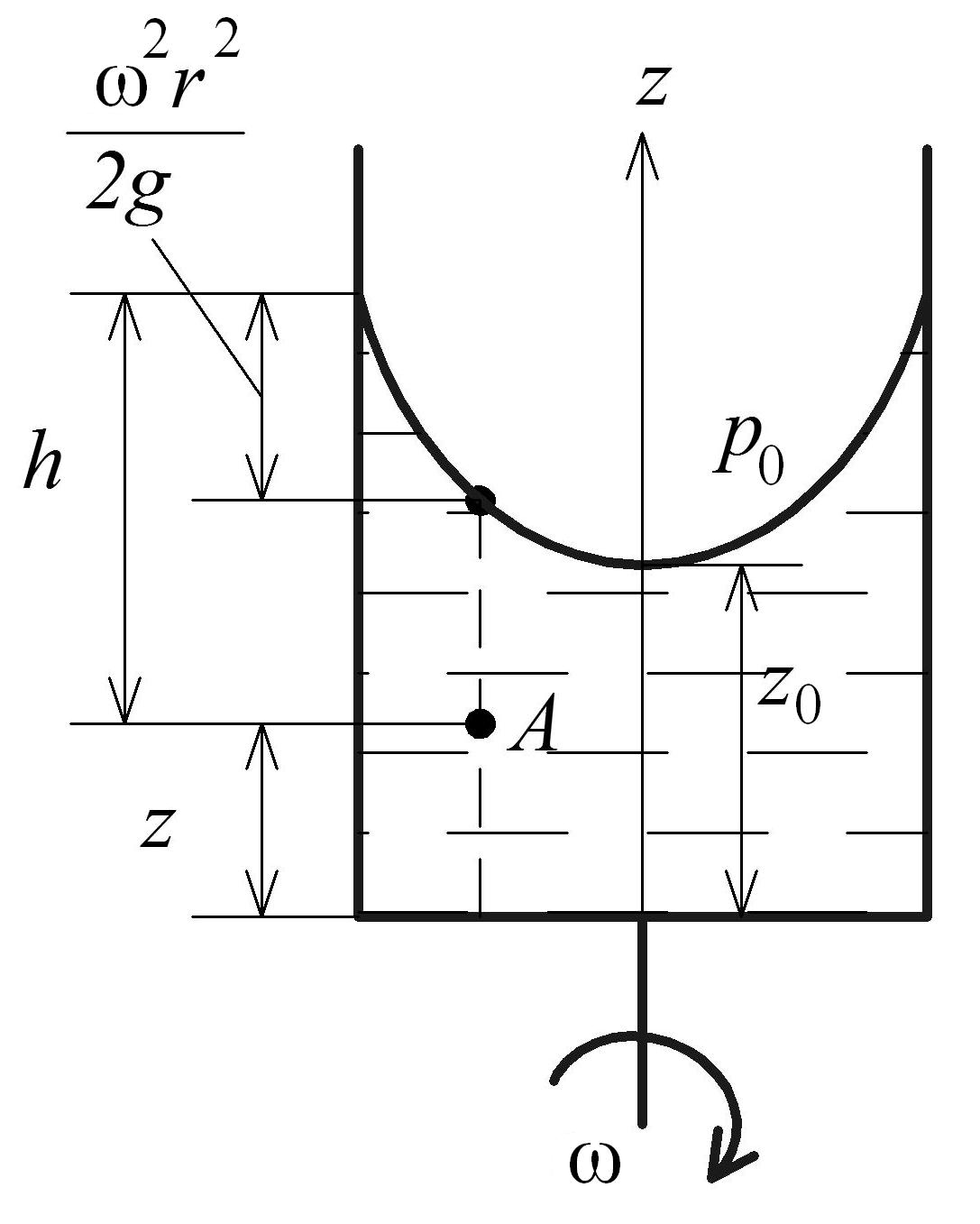
Рис. 1.14. Равновесие жидкости во вращающемся сосуде
Для решения задачи перейдем к цилиндрической системе координат r, , z. Нетрудно доказать, что:
(1.32)
где
– единичная центробежная (отнесенная
к единице массы) сила. Тогда вместо (1.3)
получим:
(1.33)
Запишем
граничное условие: при
Проинтегрировав (1.33) и воспользовавшись граничным условием, получим:
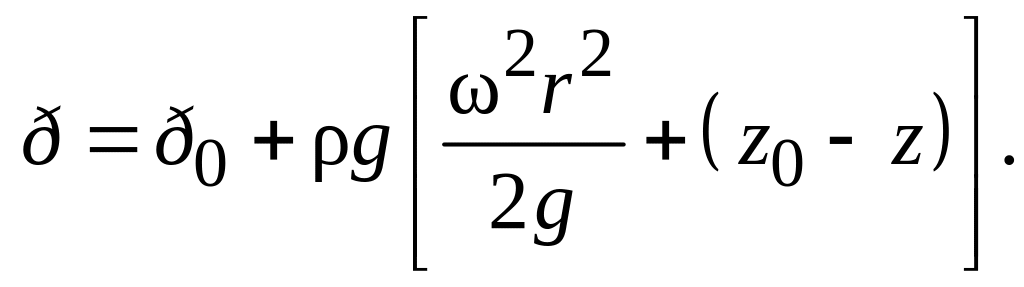(1.34)
Уравнение (1.34) представляет собой закон распределения давления внутри жидкости в зависимости от координат r и z.
Выражение
в скобках
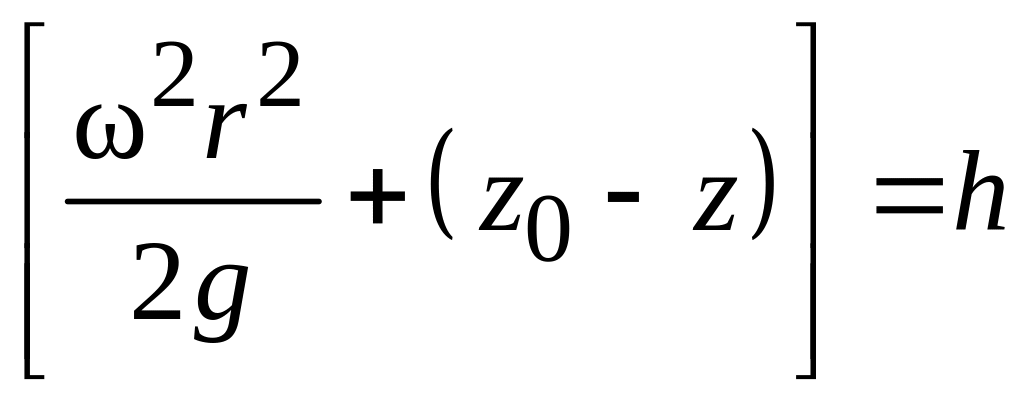представляет собой глубину погружения
рассматриваемой точки А
под свободной поверхностью. Подставляя
значение h
в уравнение (1.34),
получим:
(1.35)
Уравнение
(1.35) совпадает с уравнением (1.7), записанным
для покоящейся жидкости. Однако форма
свободной поверхности, от которой
отсчитывается глубина погружения для
уравнения (1.35), иная. Как известно, на
свободной поверхности
.
Тогда из уравнения (1.34) получим формулу
свободной поверхности в виде:
.
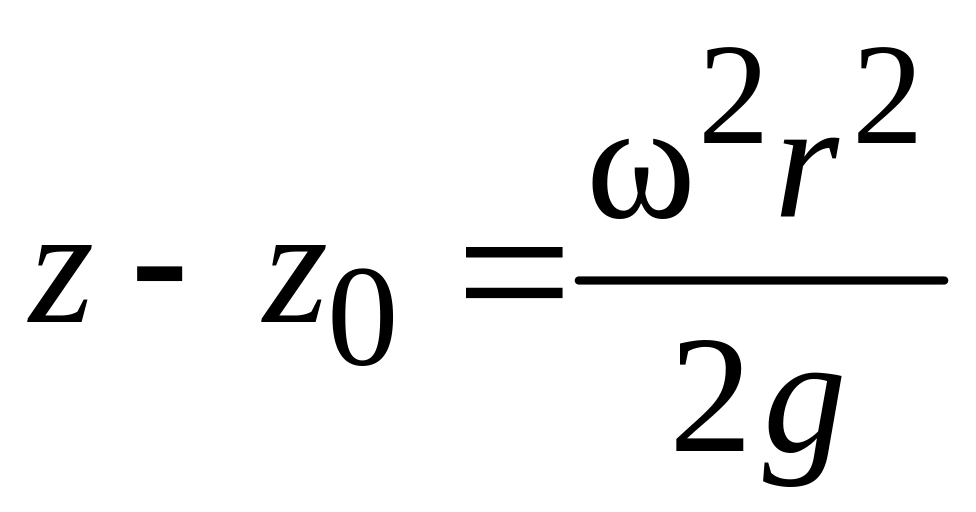(1.36)
В уравнении (1.36) z является текущей координатой свободной поверхности.
Уравнение (1.36) описывает кривую в виде параболы, а свободная поверхность, полученная на основе этой кривой, является параболоидом вращения.
На
практике чаще всего встречаются случаи,
когда
.
Тогда поверхности уровня жидкости без
большой ошибки можно считать круглыми
цилиндрами с общей осью – осью вращения
сосуда. Тогда
для давления получим
выражение:
(1.37)
где
– внутренний радиус ротора,
– радиус свободной поверхности жидкости.