4.4. Фильтрование

Фильтрованием называется процесс разделения НС при помощи пористых перегородок, задерживающих дисперсную фазу, но пропускающих дисперсионную среду (рис. 4.15).

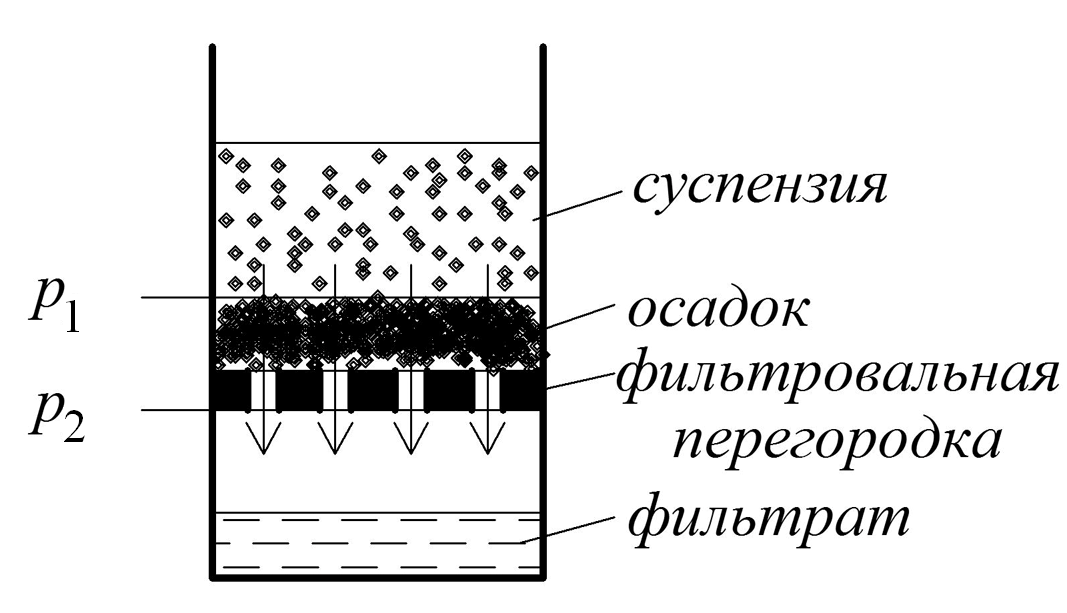
Рис. 4.15. Схема фильтра для разделения суспензий

Фильтрование применяют в промышленности для тонкого разделения ЖНС и ГНС. С его помощью можно получить значительно более полную, чем в процессах осаждения, очистку жидкости или газа от вредных примесей.

В процессе фильтрования твердые частицы либо задерживаются на поверхности фильтровальной перегородки, образуя осадок, либо проникают в её глубину, задерживаясь в порах. В соответствии с этим различают фильтрование с образованием осадка и фильтрование с закупориванием пор.

Движущей силой процесса фильтрования является разность давлений до и после фильтра. Перепад давления может быть создан полем гравитационных, центробежных сил и полем поверхностных сил давления.

Фильтровальные перегородки. Фильтровальные перегородки оказывают определяющее влияние на качество фильтрования.

Различают гибкие фильтровальные перегородки: хлопчатобумажные, шерстяные, синтетические и стеклянные ткани; сетки; нетканые материалы; негибкие: жесткие – керамика, металлокерамика, пористая пластмасса и т.п., и нежесткие – песчаные, гравийные фильтры и т.п.

В промышленности для фильтрования суспензий применяют, в основном, гибкие перегородки. При этом реализуется процесс фильтрования с образованием осадка. Фильтрование с закупориванием пор встречается при осветлении жидкостей.

Осадки. Осадки, получаемые на фильтровальной перегородке при разделении суспензий, подразделяются на несжимаемые и сжимаемые. Если порозность осадка  при увеличении разности давлений p не меняется, то осадок называется несжимаемым, и, наоборот, если с увеличением p уменьшается , то осадок сжимаемый.

Несжимаемые осадки: частицы песка, кристаллы карбоната кальция и бикарбоната кальция. Сжимаемые осадки: гидраты окисей металлов, например, алюминия, железа, меди и т.п.

Уменьшение порозности осадка  приводит к уменьшению эквивалентного диаметра канала и к резкому увеличению гидравлического сопротивления слоя осадка. Поэтому фильтрование в случае образования сжимаемых осадков проводят обычно под вакуумом.

4.4.1. Основное уравнение фильтрования

Пусть движущая сила процесса фильтрования p создана столбом жидкости или поверхностными силами давления (рис. 4.16).

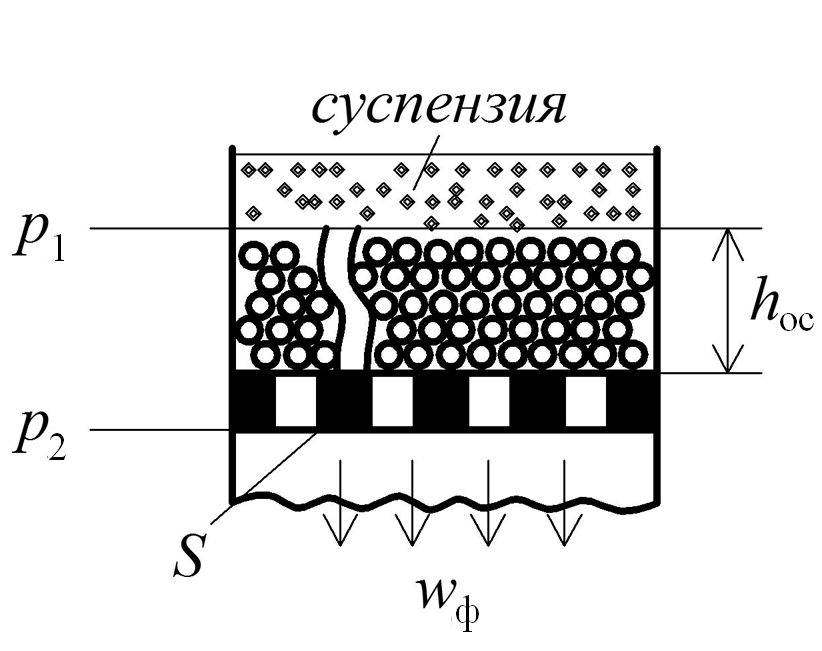
Рис. 4.16. Схема фильтровальной перегородки и осадка

Определим значение скорости фильтрования . Скорость фильтрования – это фиктивная скорость, отнесенная ко всей площади фильтрующей перегородки S. Высота слоя осадка, следовательно, и его гидравлическое сопротивление меняются с течением времени. Поэтому по времени меняется и . Переменную скорость фильтрования определим в дифференциальной форме:

, (4.13)

где V – объем фильтрата, S – площадь фильтрующей перегородки, t – продолжительность фильтрования.

Определим эту же скорость фильтрования из гидравлического сопротивления осадка. Для расчета гидравлического сопротивления неподвижного зернистого слоя была получена следующая формула:

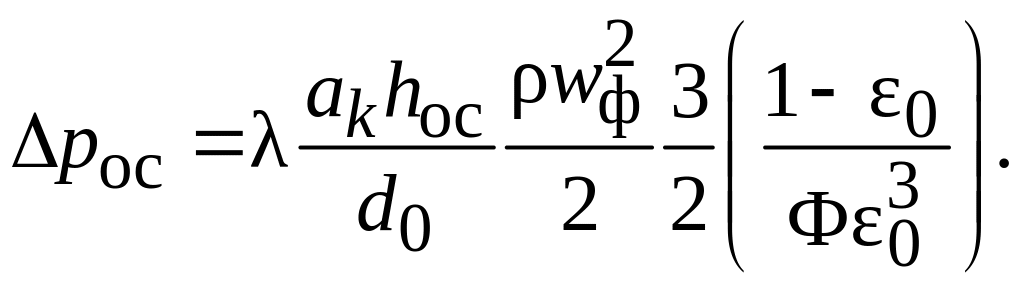(4.14)

Коэффициент сопротивления определяется:

,

где

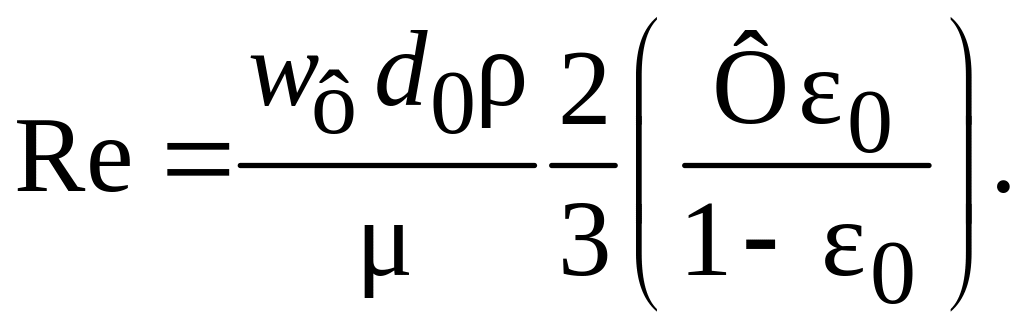
Обычно ввиду небольшого размера пор в слое осадка, а также малой скорости движения жидкой фазы в порах можно считать, что фильтрование в пределах осадка проистекает в ламинарном режиме. При малых значениях Re вторым членом зависимости для  можно пренебречь. С учетом этого уравнение (4.14) можно записать в виде:

,

(4.15)

где – сопротивление слоя осадка,  – вязкость фильтрата.

Аналогичная формула может быть записана и для фильтрующей перегородки:

(4.16)

Для получения полного гидравлического сопротивления фильтра, который равняется , необходимо сложить гидравлические сопротивления осадка и фильтрующей перегородки:

(4.17)

Для случая, если , из (4.17) найдем :

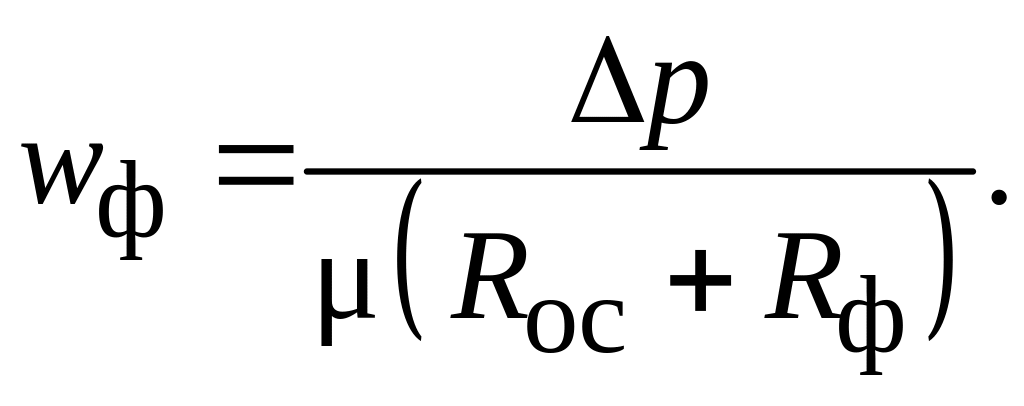(4.18)

Приравнивая (4.13) и (4.18), получим:

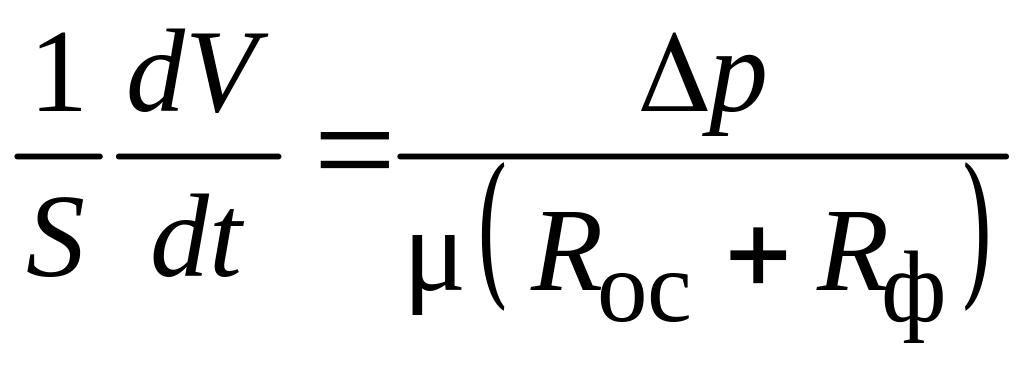. (4.19)

Сопротивление фильтровальной перегородки может быть принято постоянной величиной. Считаем, что при процессе с образованием осадка в порах фильтровальной перегородки изменений не происходят. В процессе фильтрования величина меняется непрерывно, от нуля вначале и до максимального значения в конце процесса. Установим связь с объемом фильтрата . Учитывая пропорциональность объемов осадка и фильтрата можно записать:

(4.20)

где – коэффициент пропорциональности, – высота слоя осадка.

Представим сопротивление осадка в виде:

(4.21)

где – удельное объемное сопротивление слоя осадка. Подставляя значение из (4.20) в (4.21), получим:

(4.22)

Перепишем уравнение (4.19) с учетом (4.22):

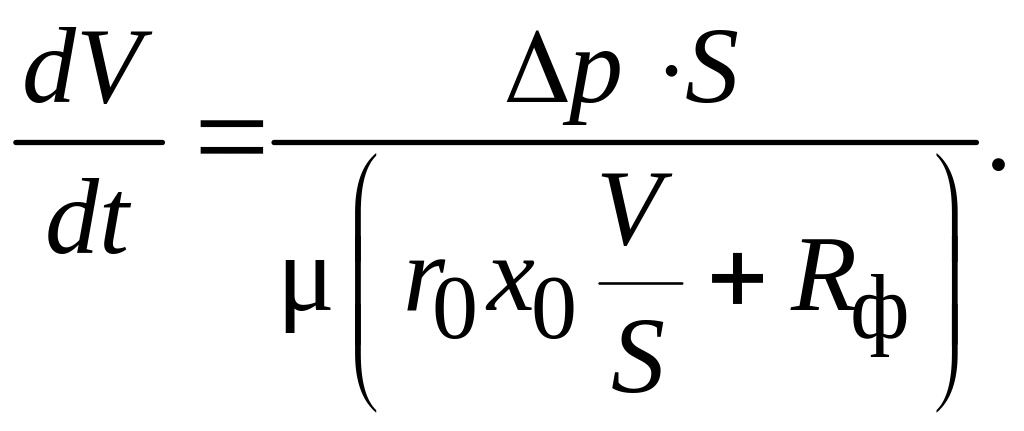(4.23)

Это и есть основное уравнение фильтрования. Из уравнения (4.23) видно, что производительность фильтра зависит прямо пропорционально от перепада давления p. Производительность фильтра увеличивается с уменьшением вязкости фильтрата и уменьшается с ростом толщины осадка и сопротивления фильтровальной перегородки.

Рассмотрим два технологических процесса фильтрования: и .

Пусть . Этот случай реализуется, когда фильтрование идет за счет сжатого воздуха или вакуумирования.

В уравнении (4.23) разделим переменную и проинтегрируем левую часть уравнения в пределах от 0 до V, а правую – от 0 до t.

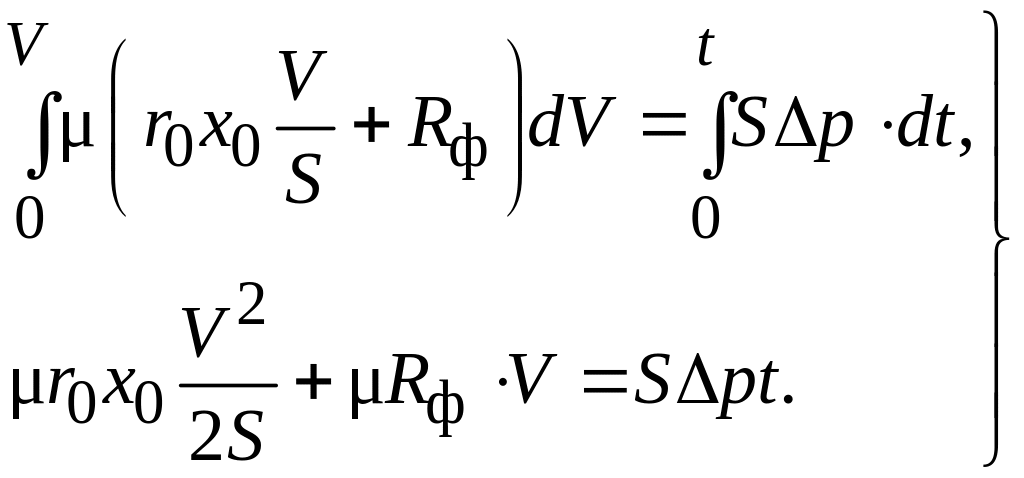(4.24)

Преобразуем второе уравнение (4.24), приведя его в удобный для использования вид:

(4.25)

Уравнение (4.25) может быть использовано для практических целей, если известны , и . Эти величины называются константами процесса фильтрования. Их можно определить экспериментально.

На практике часто встречаются случаи, когда . Тогда вторым членом левой части уравнения (4.25) можно пренебречь:

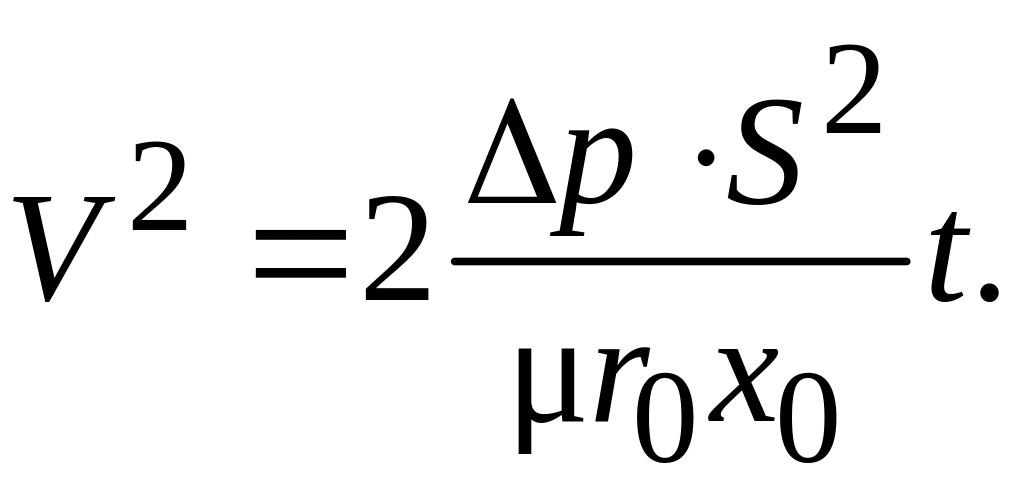(4.26)

Уравнения (4.25) и (4.26) применимы как к сжимаемым, так и к несжимаемым осадкам, поскольку при значения и в процессе фильтрования остаются постоянными.

Пусть w_ф = const. Такой рабочий режим осуществляется путем нагнетания суспензии поршневым насосом. Сопротивление, встречаемое потоком фильтрата, растет с ростом толщины осадка . Поэтому постоянство может быть обеспечено лишь при непрерывном росте разности давлений p. При постоянной скорости фильтрования отношение может быть заменено отношением . Тогда получим:

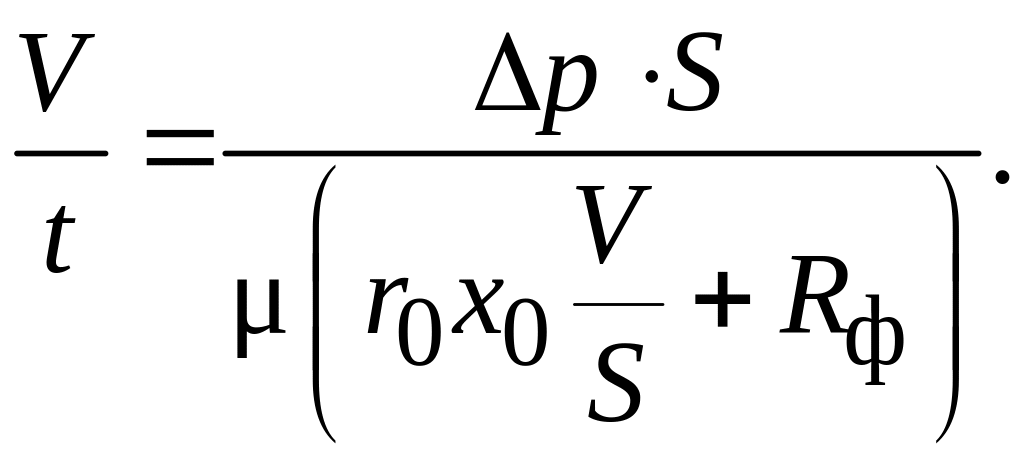(4.27)

Уравнение (4.27) может быть приведено к виду:

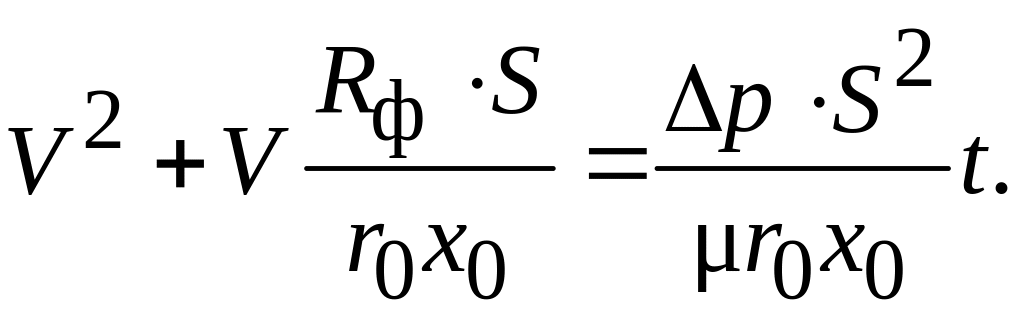(4.28)

Для случая, когда из (4.28) получим:

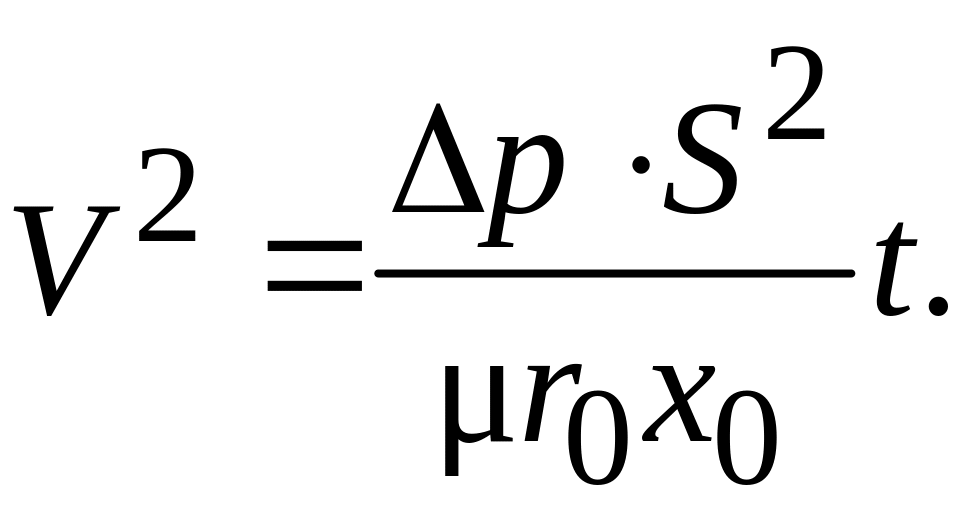(4.29)

Из уравнения (4.28) с учетом найдем необходимый перепад давления для проведения процесса фильтрования:

(4.30)

Уравнения (4.28)–(4.30) применимы к несжимаемым осадкам. При использовании их для сжимаемых осадков необходимо учесть зависимость удельного сопротивления осадка от p.