3.1.3. Псевдоожиженный слой

При достижении скорости потока слой перестает быть неподвижным, его порозность и высота начинают увеличиваться, слой приобретает текучесть и переходит во взвешенное состояние. В таком слое твердые частицы интенсивно перемешиваются в различных направлениях. Двухфазная система приобретает свойства капельной жидкости (течет, имеет поверхность раздела). Такой слой зернистого материала называется псевдоожиженным слоем, а соответствующее состояние – режимом псевдоожижения.

Скорость называется скоростью начала псевдоожижения. С дальнейшим ростом скорости слой продолжает расширяться, и интенсивность движения частиц увеличивается, одновременно увеличивается и порозность, приближаясь к верхней границе – единице. При слой настолько разрыхляется, что частицы движутся практически независимо друг от друга и сила сопротивления отдельной частицы P становится равной её весу за вычетом архимедовой подъемной силы. Скорость называется скоростью витания. Дальнейшее увеличение скорости приведет к уносу частиц из аппарата.

Итак, пределы существования режима псевдоожижения: (рис. 3.3).

Для режима псевдоожижения гидравлическое сопротивление слоя остается практически постоянным. В начале псевдоожижения для того, чтобы оторвать частицы друг от друга, требуется некоторое избыточное давление (точка А). На практике псевдоожиженный слой создается при некотором значении рабочей скорости , находящейся в пределах Отношение называется числом псевдоожижения. Часто принимают k = 2.

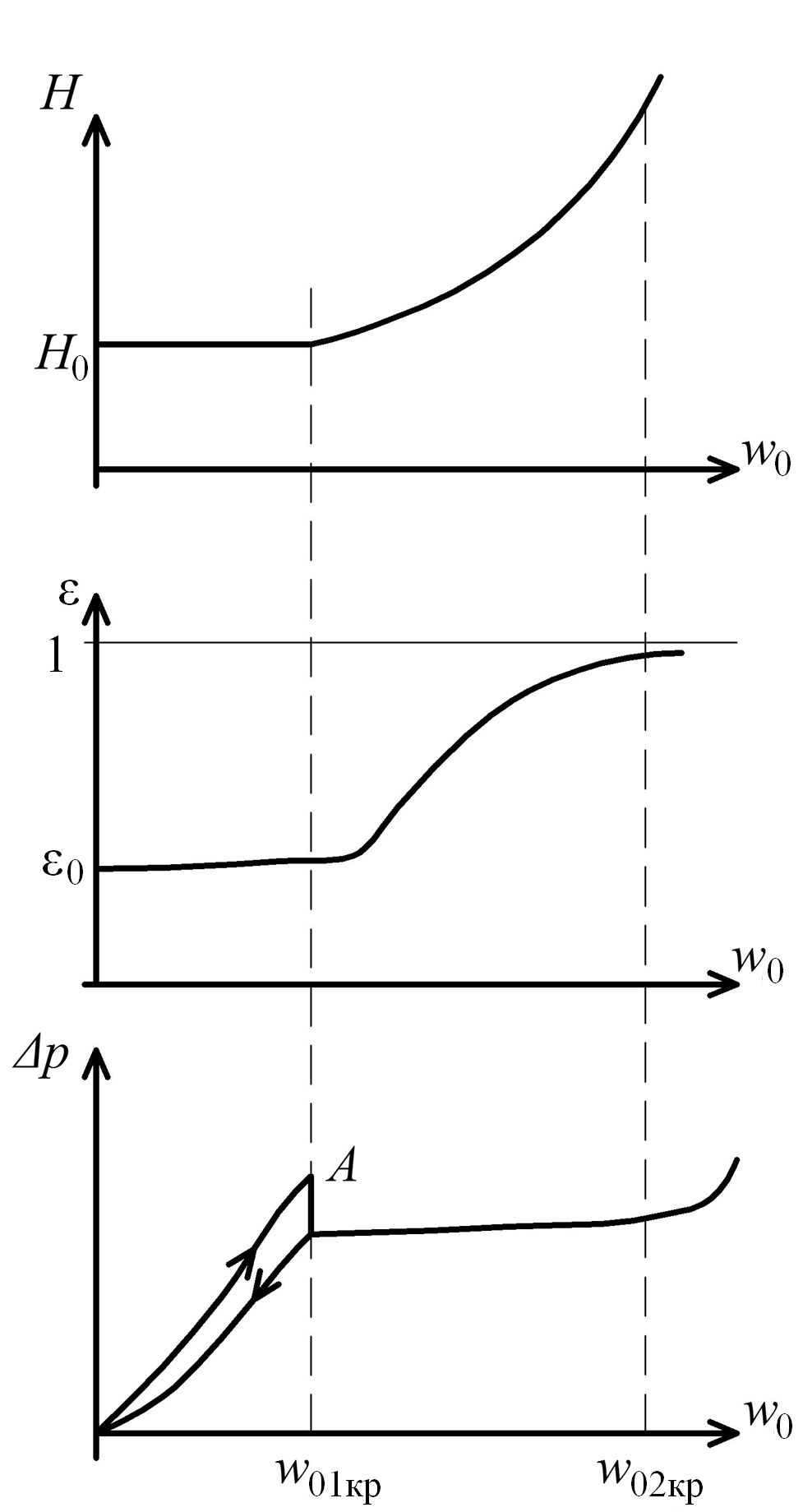
Рис. 3.3. Изменение параметров зернистого слоя от фиктивной скорости

Определим скорость начала псевдоожижения расчетным путем. Уравнение (3.5) можно представить в виде:

(3.17)

С другой стороны, это же давление может быть определено из уравнения (3.14) при :

(3.18)

Приравнивая (3.17) и (3.18), находим:

(3.19)

Приближенное решение уравнения (3.19), где , для модифицированного числа Рейнольдса при котором начинается псевдоожижение, дает:

(3.20)

Здесь – критерий Архимеда.

Порядок расчета :

– находим критерий Архимеда;

– по формуле (3.20) определяем модифицированный критерий Рейнольдса;

– по формуле находим .

3.1.4. Расчет скорости витания (осаждения) и уноса

При скорости потока порозность приближается к единице. Поэтому можно рассматривать взаимодействие потока жидкости и отдельной частицы. Скорость соответствует верхней границе режима псевдоожижения, при этом частица неподвижно витает в потоке. Эту скорость называют скоростью витания . Для случая витания вес частицы полностью уравновешивается силовым воздействием жидкостного потока. Этот случай силового взаимодействия реализуется и для случая, когда твердая частица падает с постоянной скоростью , называемой скоростью осаждения, в неограниченном объеме неподвижной среды. Следовательно = .

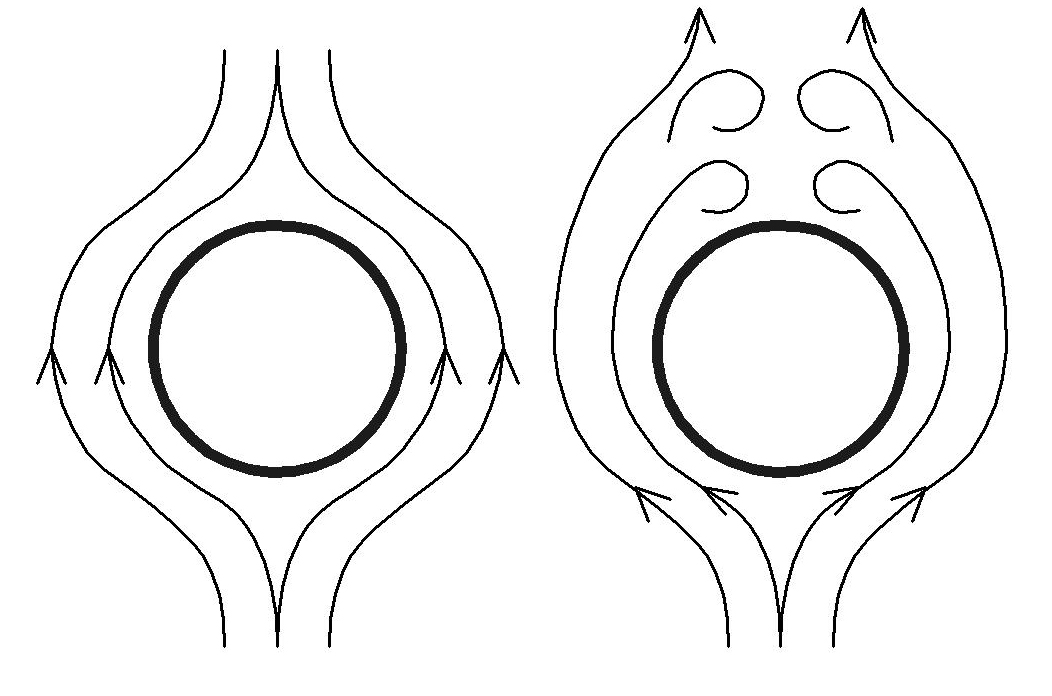
При ламинарном обтекании тела сопротивление потока зависит в основном от вязкости среды; при турбулентном – от поверхности тела отрываются вихри, которые создают за ним область пониженного давления (рис. 3.4).

а) б)

Рис. 3.4. Обтекание потоком сферы:

а – ползущее течение; б – отрыв пограничного слоя

Рассмотрим осаждение сферической частицы диаметром . Запишем условие равновесия сил:

(3.21)

где – сила сопротивления потока, – вес частицы, – выталкивающая (архимедова) сила. Силу можно выразить по аналогии с потерянным давлением с использованием коэффициента гидравлического сопротивления :

(3.22)

где S – площадь поперечного сечения сферы ,  – плотность среды,  – коэффициент гидравлического сопротивления.

Для сферы очевидно:

(3.23)

где – плотность твердой частицы. Тогда получим:

(3.24)

Из (3.24) найдем значение :

(3.25)

Рассмотрим более подробно коэффициент гидравлического сопротивления . Силу сопротивления потока можно представить в виде суммы сил лобового сопротивления и сопротивления трения :

(3.26)

Тогда и коэффициент гидравлического сопротивления  может быть выражен зависимостью:

(3.27)

где – коэффициент лобового сопротивления, – коэффициент сопротивления трения.

При ламинарном течении частица плавно обтекается потоком жидкости (ползущее течение) и энергия расходуется только на преодоление трения. С увеличением скорости потока всё большую роль играет лобовое сопротивление, и с какого-то момента сопротивлением трения можно будет пренебречь. Тогда увеличение скорости потока не приведет к изменению , наступает автомодельный режим (рис. 3.5).

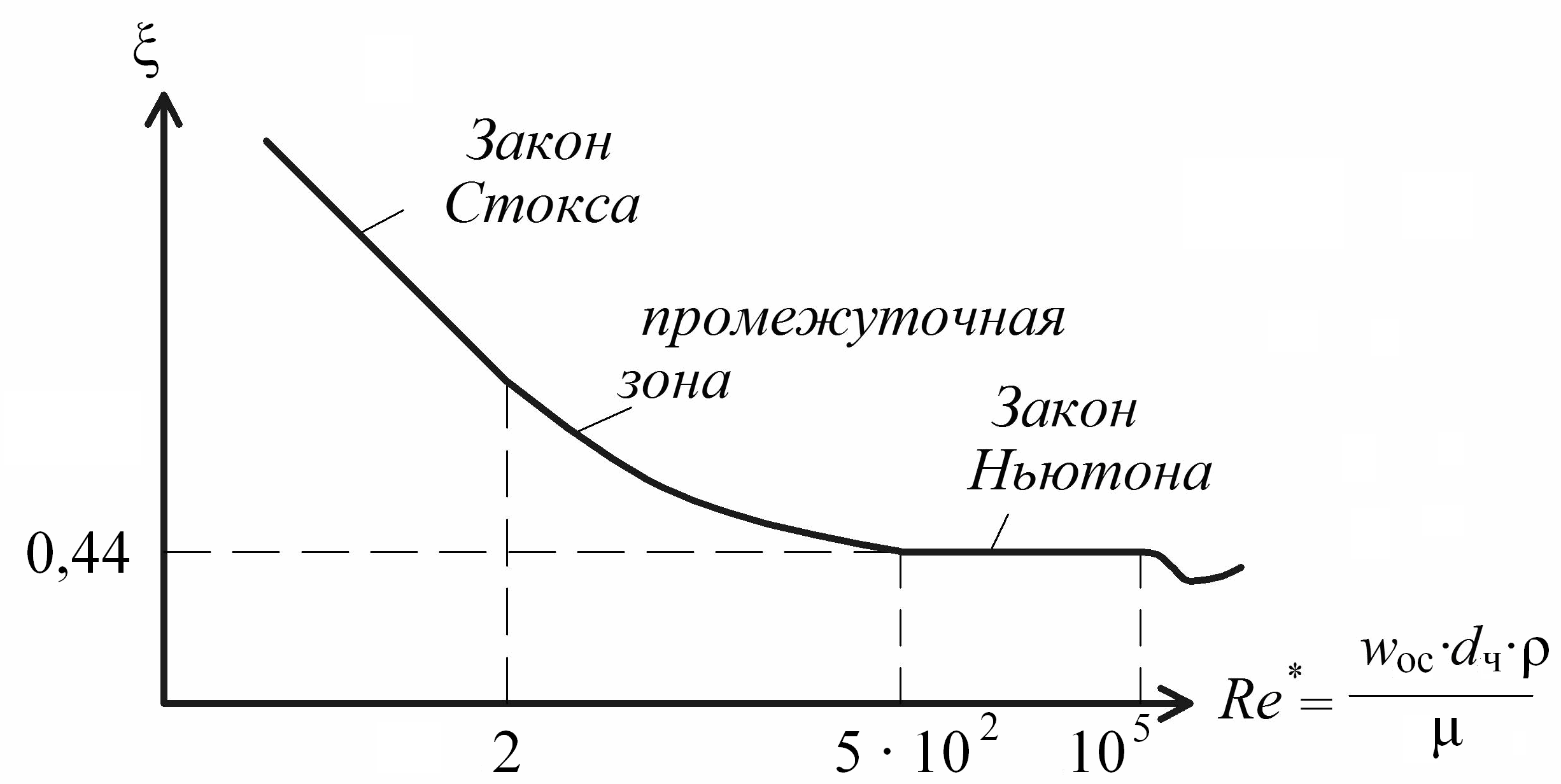
Рис. 3.5. Зависимость коэффициента гидравлического сопротивления  от режима обтекания сферы

Для случая ламинарного режима осаждения можно получить теоретическим путем значение :

(3.28)

Тогда из (3.35) получим:

(3.29)

Полученная зависимость называется законом осаждения Стокса. Закон Стокса справедлив для области . В области действия закона Ньютона (в условиях автомодельности критерия ) коэффициент гидравлического сопротивления Тогда из (3.25) будем иметь:

(3.30)

В промежуточной области для  предлагается следующая формула:

(3.31)

Для того чтобы определить режим обтекания частицы потоком жидкости и, следовательно, выбрать формулу для расчета скорости , необходимо знать величину , а содержит искомую величину . Задачу можно решить методом последовательных приближений. Однако этого трудоемкого процесса можно избежать. Преобразуем уравнение (3.25), вводя критерии и Ar, и получим:

(3.32)

Из (3.32) определим границы промежуточной зоны по критерию Архимеда Ar:

для получим Ar = 36;

для получим Ar = 8,3 · 10⁴.

Как известно, критерий Архимеда не содержит искомую величину .

Тогда можно предложить следующий порядок расчета скорости витания (осаждения):

– определяем значения критерия Архимеда Ar;

– определяем зону расчета  и выбираем расчетную формулу;

– для данной зоны по соответствующей формуле определяем значение скорости .

Скорость осаждения частиц несферической формы меньше, чем у сферических частиц:

w'_ос = _ф w_ос.

Здесь _ф < 1 – коэффициент формы, значение которых определяется опытным путем. Например, для округлых частиц _ф = 0,77, угловатых – _ф = 0,66, продолговатых – _ф = 0,50 и пластинчатых – _ф = 0,46. Коэффициент формы связан с фактором формы соотношением _ф = ^–2.

Скорость стесненного осаждения меньше скорости одиночной частицы за счет соударения твердых частиц друг о друга.

Для приближенного определения при всех режимах движения частиц можно использовать универсальную формулу Тодеса:

(3.33)

При скоростях потока жидкости, превышающих критическую скорость , происходит разрушение псевдоожиженного слоя и вынос частиц из аппарата. Скорость потока, при которой происходит массовый унос твердых частиц из аппарата, называют скоростью уноса . Скорость уноса всегда больше скорость витания .

Осаждение твердых частиц под действием центробежных сил. Осаждение твердых частиц под действием центробежных сил происходит более интенсивно. Интенсивность осаждения оценивается фактором разделения как отношение центробежной силы к силе тяжести :

(3.34)

где  – угловая скорость вращения, r – радиус вращения. Для расчета центробежной скорости осаждения применяют те же формулы, что и для осаждения в поле сил тяжести, но с учетом фактора разделения:

(3.35)

Исходное критериальное уравнение для этого случая имеет вид:

(3.36)

C учетом уравнения (3.36) устанавливаются зоны центробежного осаждения: