3.1.2. Движение жидкости через неподвижный зернистый слой

При прохождении жидкости через слой зернистого материала в качестве параметра, характеризующего движение, берется фиктивная скорость , отнесенная ко всей площади аппарата: .

Наблюдениями установлено, что при малых скоростях движения жидкости , не превышающих некоторого значения , слой неподвижен, высота слоя и порозность остаются постоянными . Жидкость движется по извилистым каналам, образованным поверхностями частиц (рис. 3.2).

Этот режим называется режимом фильтрации. Установим границы этого режима. С ростом скорости при достижении некоторого значения , частицы слегка отодвигаются друг от друга, объем слоя несколько увеличивается. Этот момент характеризуется тем, что сила давления потока на слой сравнима с силой тяжести всех частиц:

(3.5)

где – гидравлическое сопротивление слоя, – плотность частица,  – плотность жидкой среды. Скорость является верхним пределом существования неподвижного зернистого слоя, т.е. режима фильтрации.

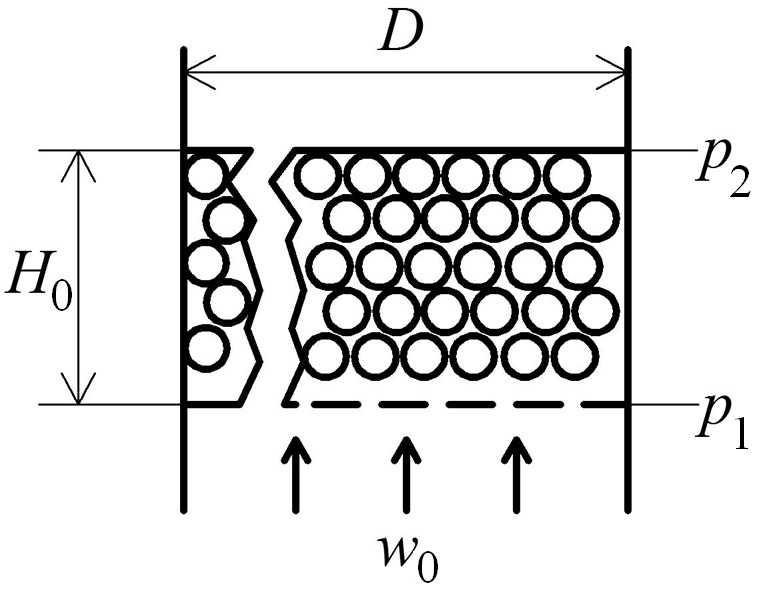
Рис. 3.2. Слой неподвижного зернистого материала

Для нижнего и верхнего живого сечений аппарата давления, соответственно, и . Они общие для всех капилляров. Если мы определим сопротивление для одного капилляра, то это и будет гидравлическим сопротивлением для всего зернистого слоя. Запишем уравнение Дарси – Вейсбаха для одного капилляра:

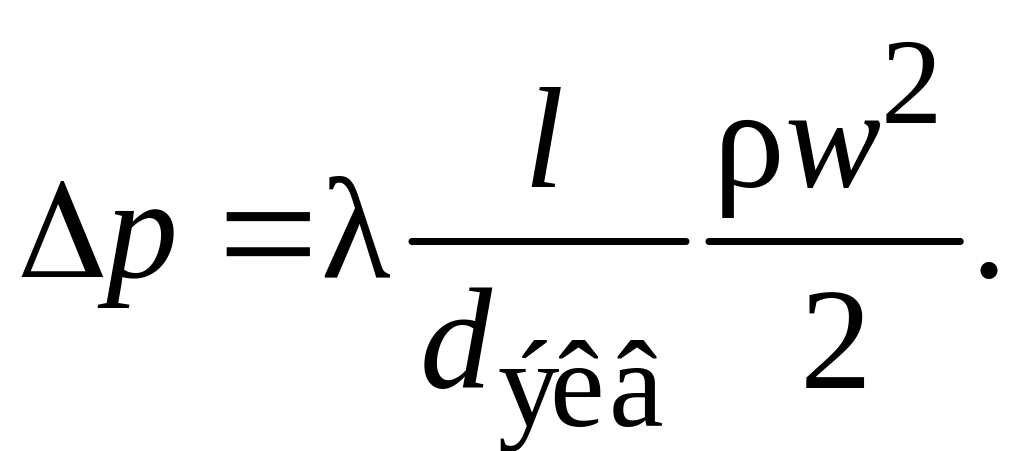(3.6)

Здесь  – коэффициент сопротивления капилляра, учитывающий все виды потерь (на трение, местные), l – длина капилляра, – эквивалентный диаметр капилляра, w – действительная средняя скорость движения жидкости по капилляру.

Определим неизвестные величины, входящие в (3.6), через известные.

Если средняя длина капилляров представляет собой высоту слоя в раз, то средняя длина капилляра . Коэффициент кривизны капилляра . Как известно, определяется как учетверенное отношение живого сечения потока на смоченный периметр.

Для нашего случая свободное сечение слоя составляет , а смоченный периметр свободного слоя – . Итак, для эквивалентного диаметра капилляра получим:

(3.7)

Эквивалентный диаметр может быть выражен также через размер частиц зернистого слоя . Пусть в объеме слоя V имеется n частиц. Объем частиц , а их поверхность – . Средний объем одной частицы:

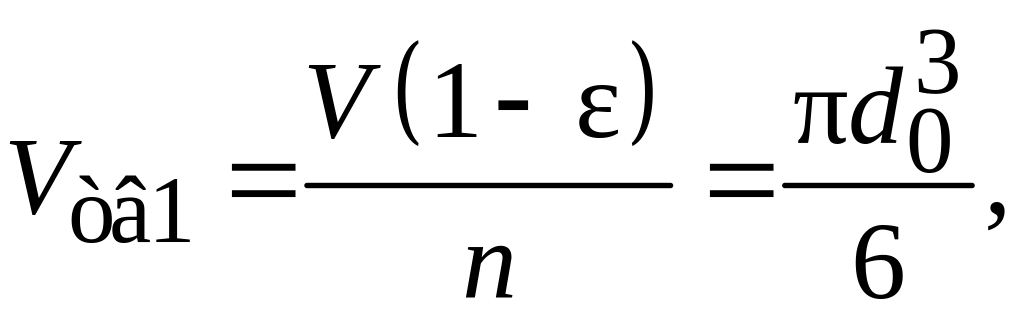(3.8)

а её поверхность

(3.9)

Из соотношений (3.8) и (3.9) найдем а:

(3.10)

Подставим в (3.7) значение а из (3.10) и найдем:

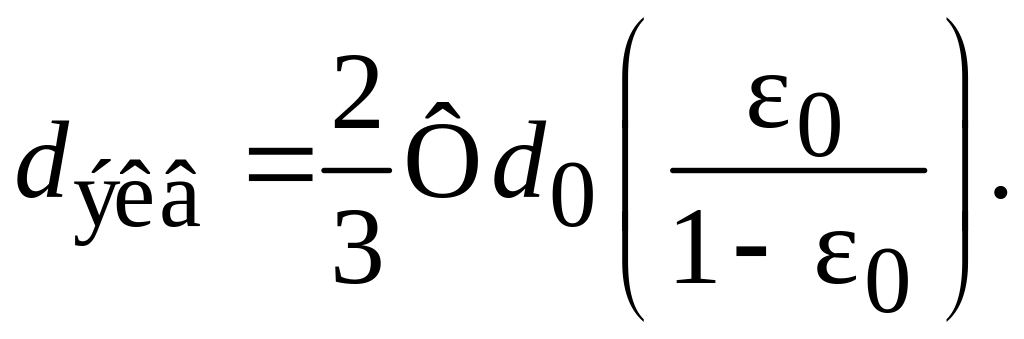(3.11)

Для нахождения истинной скорости w запишем уравнение неразрывности:

(3.12)

где – свободное сечение слоя, 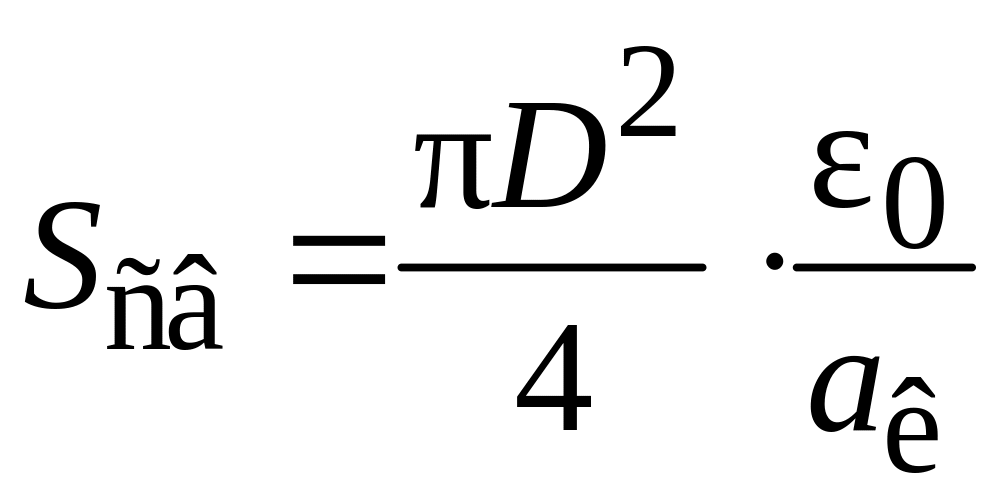. Принимая , найдем:

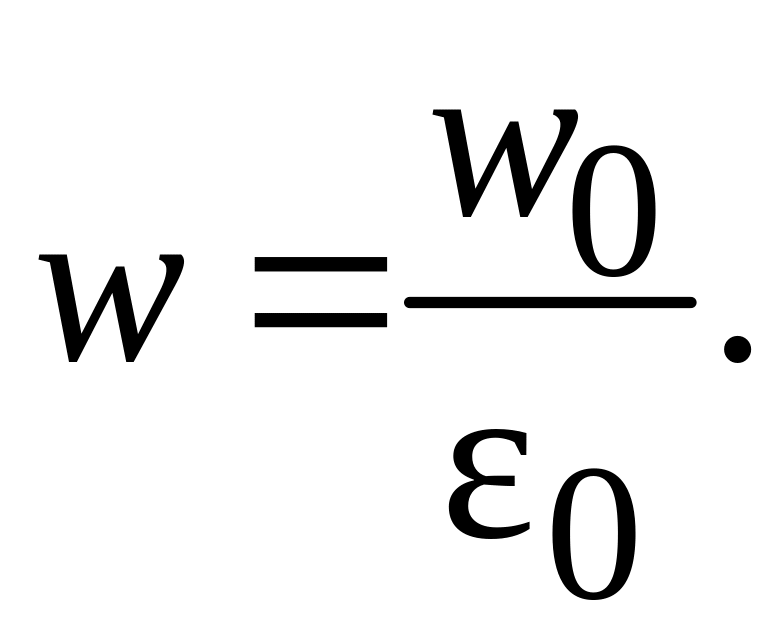(3.13)

С учетом приведенных зависимостей уравнение (3.6) примет вид:

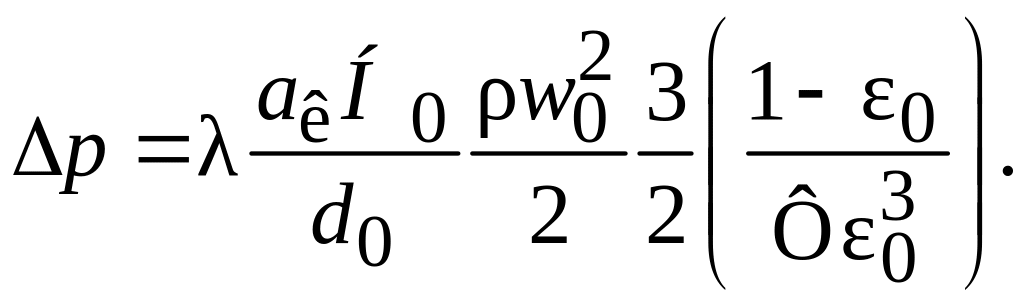(3.14)

Коэффициент сопротивления  зависит от гидродинамического режима течения жидкости в капилляре, который определяется критерием Рейнольдса:

,

(3.15)

где – модифицированный критерий Рейнольдса.

По многочисленным экспериментальным данным для всех режимов течения  можно определить по обобщенной зависимости:

(3.16)

При малых значениях Re вторым членом зависимости (3.15) можно пренебречь (в формуле (3.16) обычное Re).

При наступает автомодельный турбулентный режим. При этом  не зависит от Re и становится постоянным:

Заметим, как и для всех ламинарных течений , для турбулентных .

Значения ₀, a, Ф находятся опытным путем и приводятся в справочной литературе. Так, при свободной засыпке слоя шарообразных частиц получено