2.8. Некруглые трубопроводы

Для транспорта жидкостей в ряде случаев используются трубопроводы некруглого сечения. В таких трубах возникает сложная структура потока, в частности вторичные течения. Рассмотрим пример.

На рис. 2.31 для треугольного сечения показаны линии равных скоростей и вторичные течения в плоскости поперечного сечения трубы. Накладываясь на продольное движение, вторичное течение непрерывно переносит количество движения по направлению к углам, в результате чего в угловых участках наблюдаются сравнительно высокие продольные скорости.

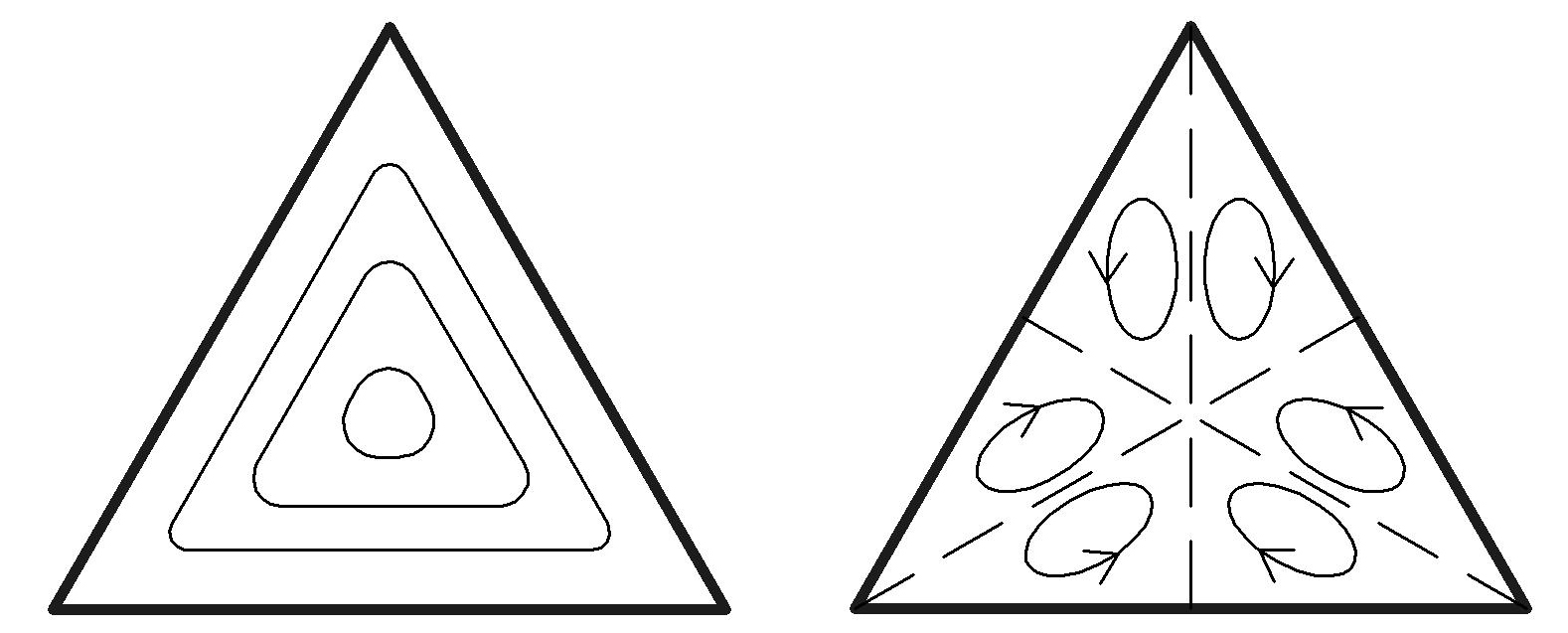
Рис. 2.31. Линии постоянных скоростей (изотахи)

и вторичные течения в треугольной трубе

Такого рода структуры потока можно получить и для других некруглых сечений, используя компьютерные технологии. Зная профиль скоростей, можно определить коэффициенты гидравлического сопротивления и, как следствие, потери напора.

Однако в инженерной практике применяется более простое приближенное решение: для определения потери напора в некруглых трубах применяется формула Дарси – Вейсбаха. В этой формуле в качестве диаметра трубы используется эквивалентный диаметр:

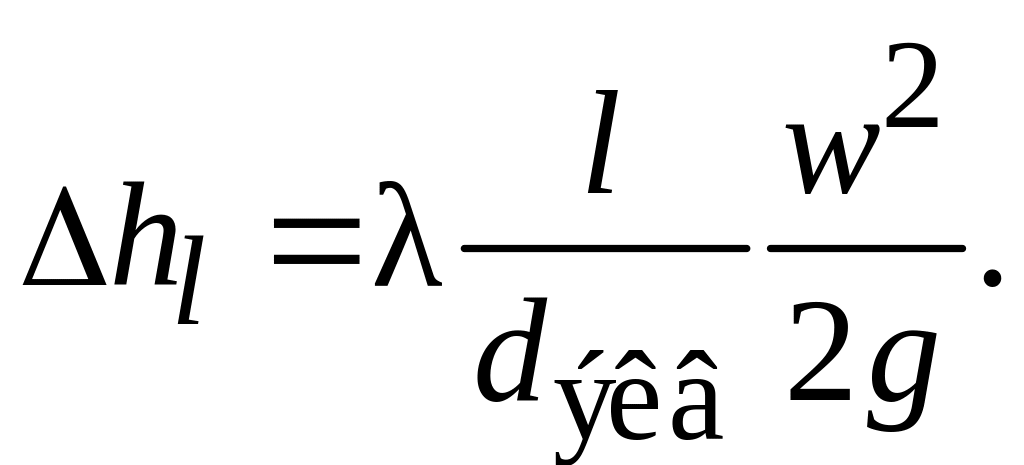(2.99)

Здесь , .

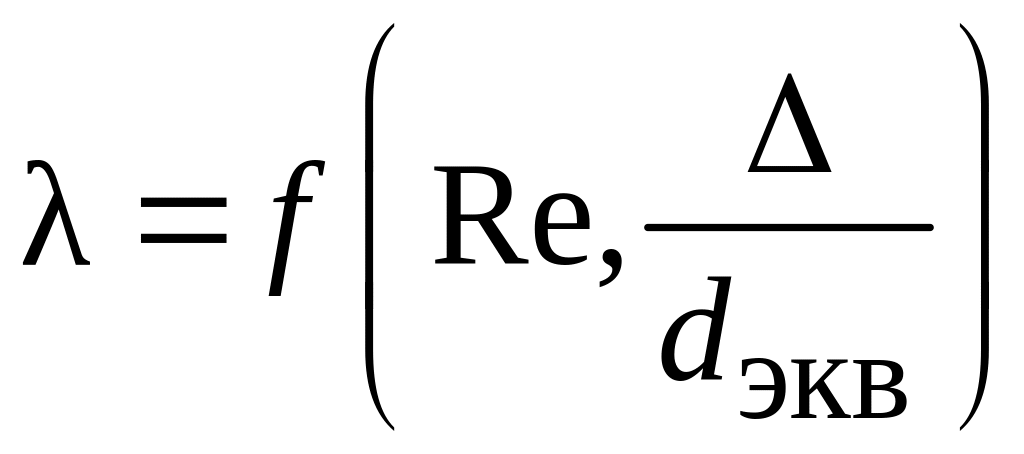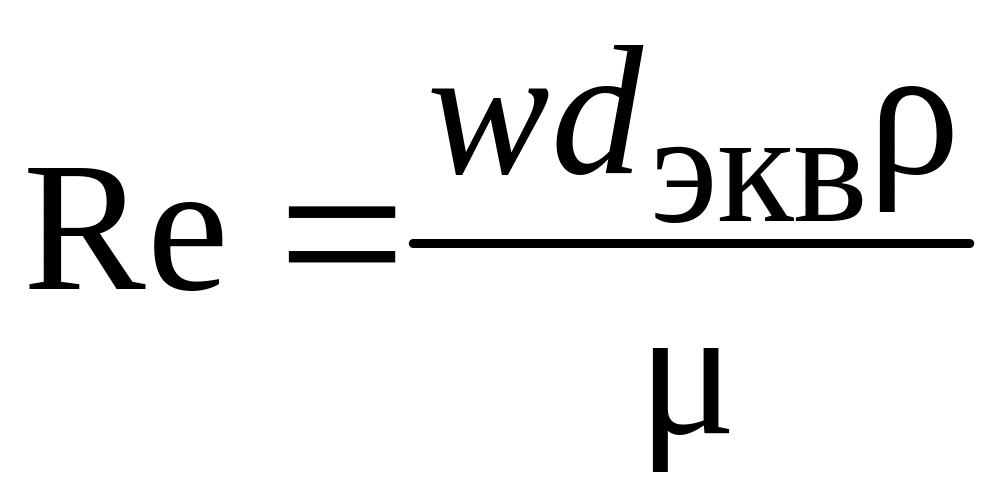Для расчета коэффициента гидравлического трения  используются те же формулы, которые были приведены раньше для круглого сечения.

Таким образом, при гидравлическом расчете некруглых трубопроводов используется тот же алгоритм расчета, что и для круглых трубопроводов, но вместо диаметра принимается эквивалентный диаметр.

Для равностороннего треугольника разница между результатами точного решения и приближенного составляет не более 10 .

2.9. Определение оптимального диаметра трубопровода

При проектировании трубопроводных систем часто возникают проблемы определения оптимального диаметра трубопровода . Предположим, что известны Расчетные формулы:

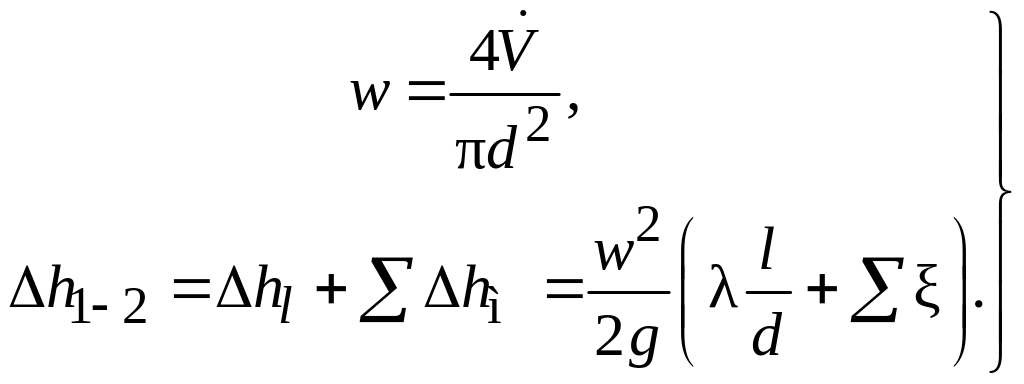(2.100)

Для ламинарного режима:

Для турбулентного режима:

Потребный напор системы:

(2.101)

Мощность потока:

Мощность насоса:

(2.102)

где – КПД насоса, – КПД электродвигателя.

Оптимальный (наиболее экономически выгодный) диаметр определяется на основе технико-экономических расчетов.

Уменьшение диаметра трубопровода приводит к увеличению мощности насоса N_н; увеличение d – наоборот к уменьшению N_н. Но увеличение диаметра приведет к увеличению стоимости трубопровода и строительства трубопроводной сети. Итак, необходимо учитывать как затраты эксплуатационные, так и капитальные. Эксплуатационные затраты : расход электроэнергии на работу насоса, обслуживание трубопроводной сети, ремонт сети и управленческие расходы. Капитальные затраты : стоимость насоса и трубопроводов, стоимость сооружений и амортизационные расходы. Полная стоимость варианта трубопроводной сети:

, (2.103)

где t – срок окупаемости сооружения. Обычно лет.

Таким образом, задача определения оптимального диаметра трубопровода сводится к определению минимума полной стоимости трубопроводной сети С. Задача может быть решена разными методами:

– математический (определение минимума функции С);

– графический;

– подбор вариантов.

Математический метод – это задача однопараметрической оптимизации. Определяем первую производную С по и приравниваем её к нулю; оттуда находим . При этом вторая производная должна быть больше нуля.

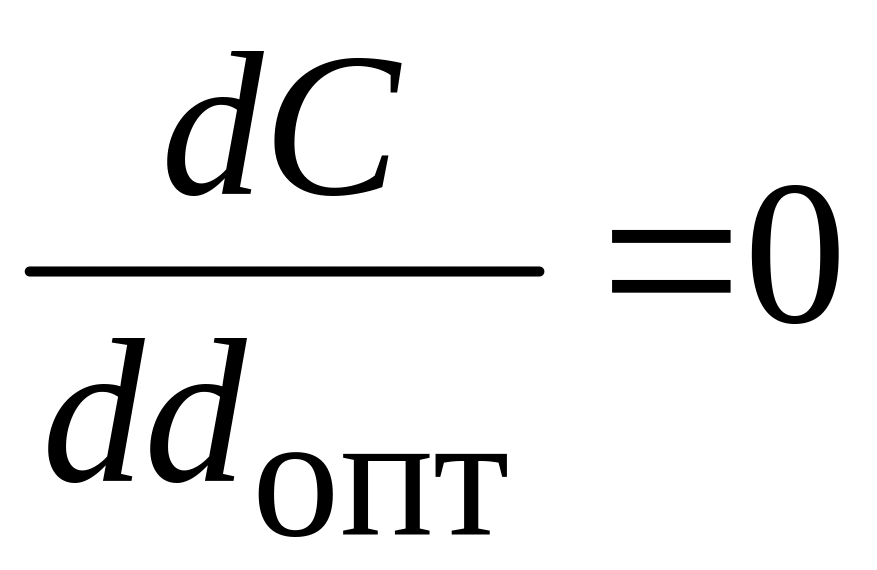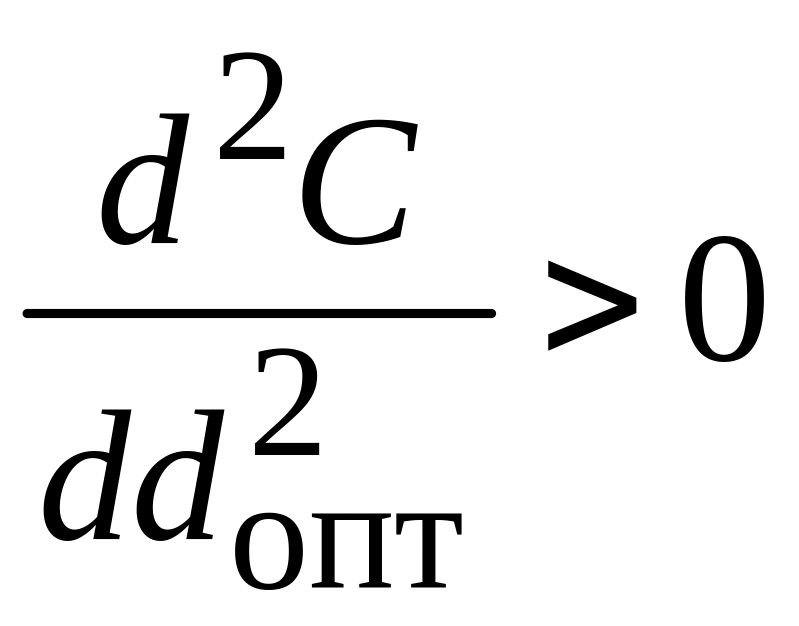, . (2.104)

Графический метод. Строим зависимости и , складываем ординаты при одинаковых d, находим минимум С (рис. 2.32).

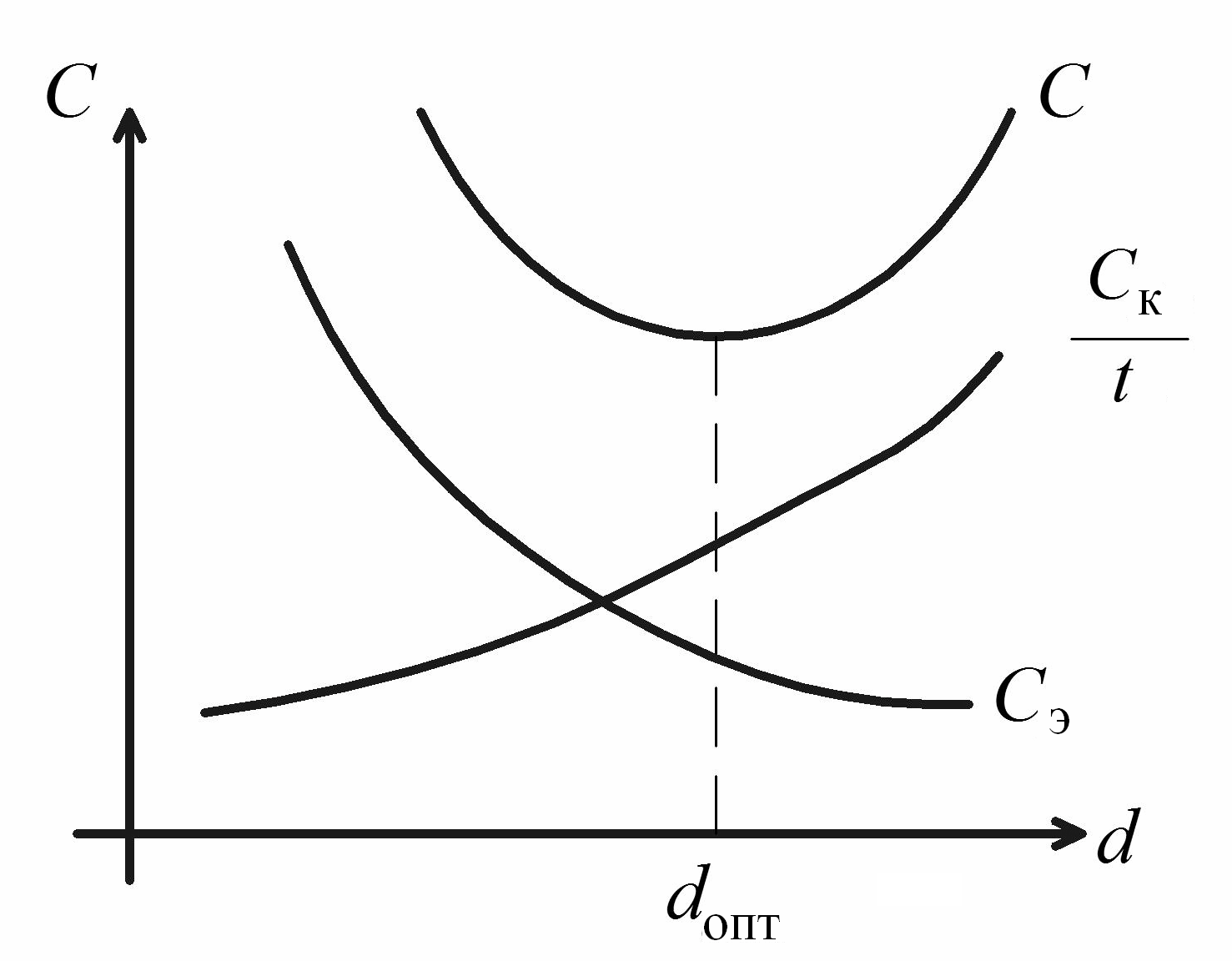
Рис. 2.32. К определению оптимального диаметра трубопровода

Подбор вариантов. Для капельной жидкости приемлемые скорости жидкости в трубопроводах колеблются в пределах w = 0,5÷3 м/с.

Найдем диаметры трубопроводов для скорости 0,5 м/с – и 3 м/с – . Определим и . будем искать в пределах от до . Далее, идя навстречу друг другу, по диаметру найдем и .

По терминологии экономистов полная стоимость варианта трубопроводной сети С – приведенная годовая затрата.