2.6. Гидравлический расчет трубопроводов, их классификация

Классификация трубопроводов. Простым называется трубопровод, состоящий из одной линии труб, с одним расходом, хотя и из разного диаметра. Все остальные трубопроводы называются сложными. На рис. 2.22 представлены (из множества возможных) наиболее распространенные схемы сложных трубопроводов. Однако эти схемы необходимо рассматривать как элементы ещё более сложных схем. Например, обеспечение водой жилого дома выглядит так: разветвленная сеть в подвале дома (в каждый подъезд), разветвленная сеть в подъезде (в каждую квартиру) и разветвление в самой квартире.

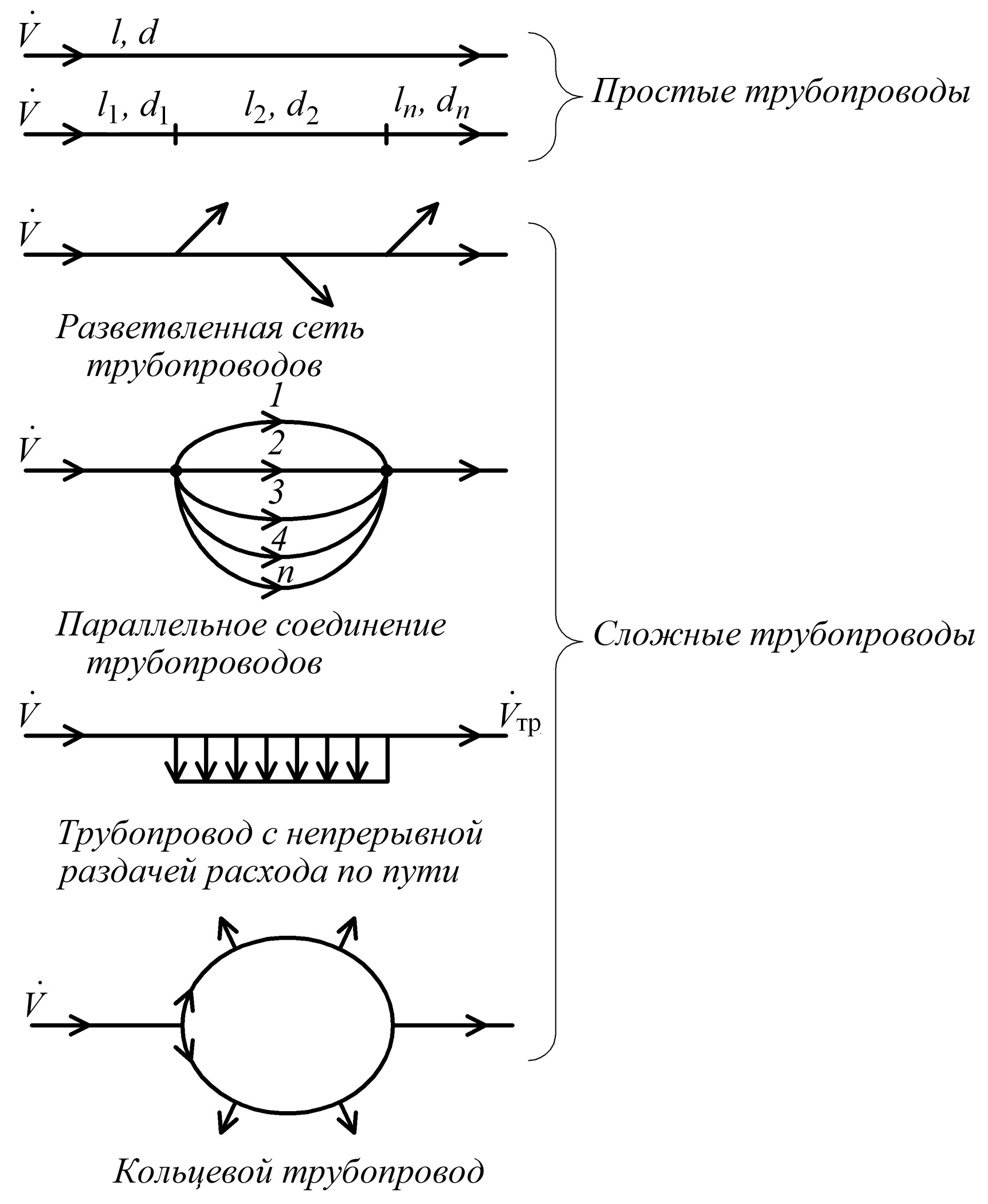
Рис. 2.22. Схемы трубопроводов

Трубопроводные схемы жилых районов города и промышленных предприятий выглядят достаточно сложно.

2.6.1. Расчет простых трубопроводов

На рис. 2.23 представлена схема простого трубопровода постоянного диаметра. На схеме определим два характерных сечения и для них напишем уравнение Бернулли. В нашем случае таковыми являются сечения 0–0 и 1–1:

(2.65)

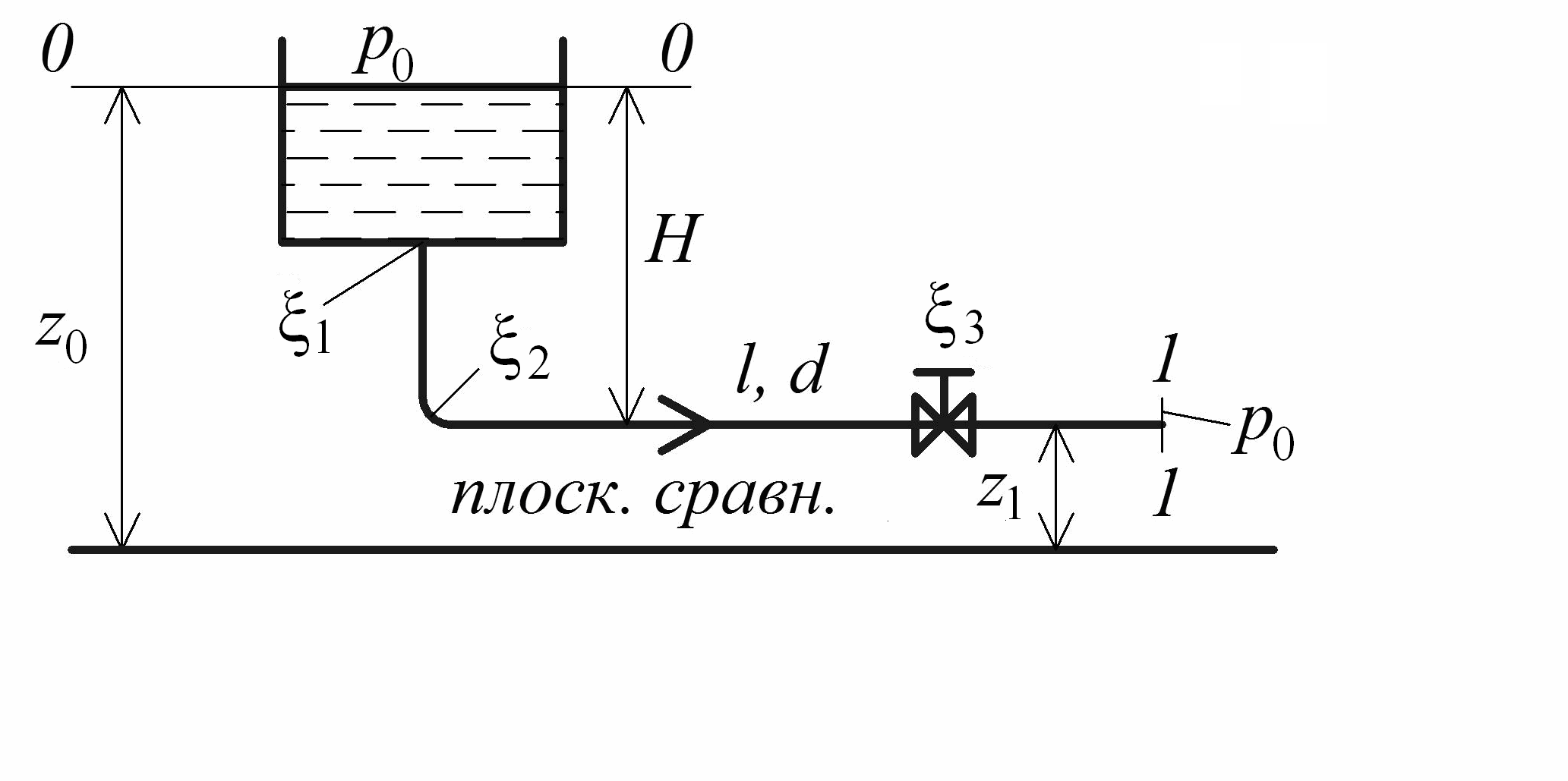
Рис. 2.23. Схема простого трубопровода

Рассмотрим члены уравнения (2.65). Обозначим давления , – скорость опускания уровня жидкости в резервуаре и – скорость движения жидкости в трубопроводе. Тогда можно записать:

(2.66)

Уравнение (2.66) можно представить в виде:

(2.67)

где Следовательно, напор Н идет на создание кинетической энергии потока (первый член правой части уравнения (2.67)) жидкости и на преодоление гидравлических сопротивлений потока.

При расчете простых трубопроводов встречается три основных типа задач:

1. Известны Необходимо найти Н.

2. Известны Необходимо найти

3. Известны Необходимо найти d.

Задача № 1. Эта задача решается путем непосредственного использования уравнения (2.66). Скорость определяется из уравнения расхода:

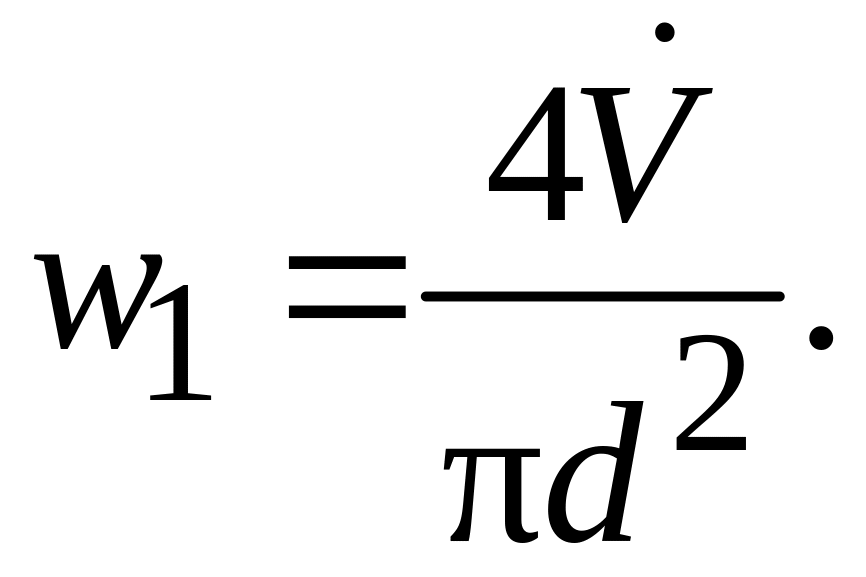(2.68)

Далее определяем .

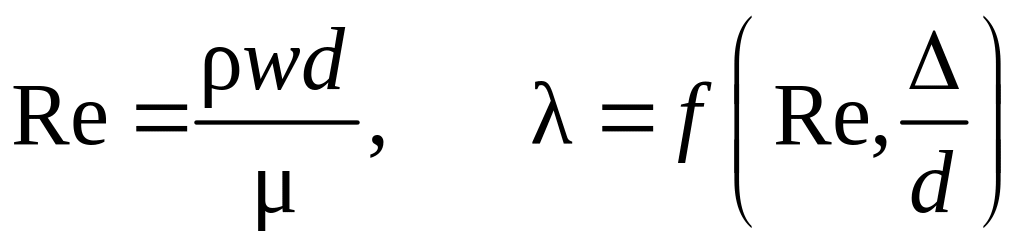Таким образом, для определения потребного напора известны все необходимые параметры потока. Эта так называемая прямая задача.

Если простой трубопровод составной, то необходимо использовать ещё уравнение неразрывности:

(2.69)

Задача № 2. Необходимо найти пропускную способность трубопровода. Воспользуемся зависимостями (2.66) и (2.68) и найдем :

(2.70)

Однако прямое определение по формуле (2.70) невозможно. Коэффициенты сопротивлений  и  зависят от режима течения жидкости в трубопроводе, а режим зависит от расхода, расход таким образом искомая величина:

Решение находим методом попыток. Если предположить, что течение развитое турбулентное, имеет место квадратичный закон сопротивления, тогда можно принимать и . Значение  для квадратичной зоны сопротивления меняется в пределах

По уравнению (2.70) находим в первом приближении. По найденному определяется Re в первом приближении, а по Re – уже более точное значение . Снова подставляют полученное  в уравнение (2.70) и находим во втором приближении. Если расхождение расходов велико, то расчет продолжают в том же порядке. Приемлемая точность обычно достигается после двух или трех приближений. Возможен графический метод решения задачи. Для составного трубопровода расчет аналогичен.

Задача № 3. Уравнения (2.66) или (2.70) относительно d не решаются. Поэтому задачу решаем приближенно, методом попыток, принимая в первом приближении, как и ранее, квадратичный закон распределения. Для этой зоны имеем:

(2.71)

По формуле (2.71) строим график Из этого графика определим , отвечающий заданному расходу (рис. 2.24).

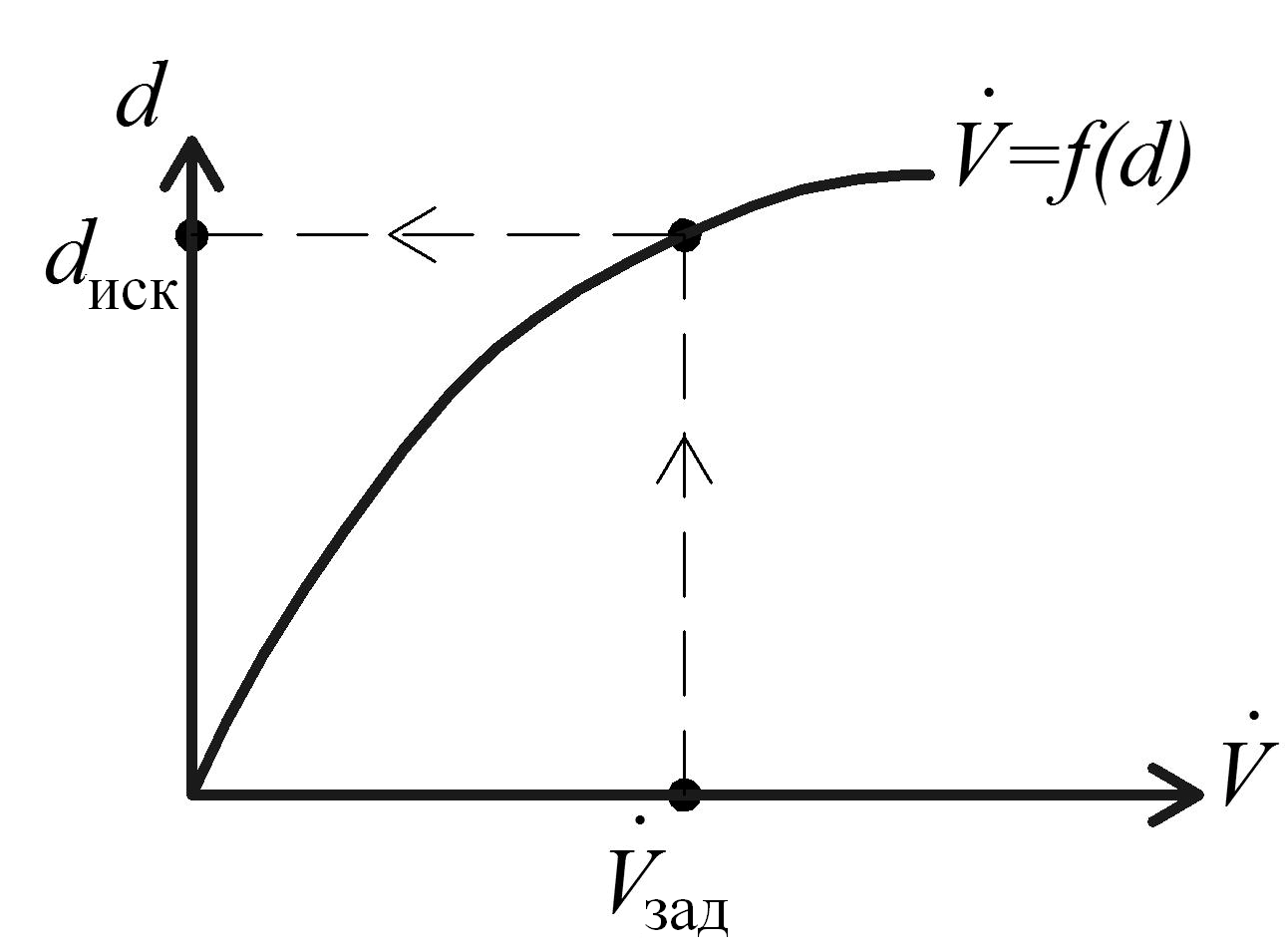
Рис. 2.24. Зависимость диаметра трубопровода от расхода

В случае составного трубопровода задача решается в том случае, если неизвестен диаметр d одного лишь участка.

Задачи 2 и 3 называются в гидравлике обратными задачами.