2.5.5. Местные гидравлические сопротивления. Интерференция местных сопротивлений

Местные гидравлические потери возникают при резкой деформации живого сечения потока и его направления. В зоне местных сопротивлений (рис. 2.21) происходит обтекание местных препятствий с образованием водоворотных зон и интенсивным обменом частицами жидкости основного потока и этих зон; транзитный поток отрывается от стенок, и возникают вихреобразования.

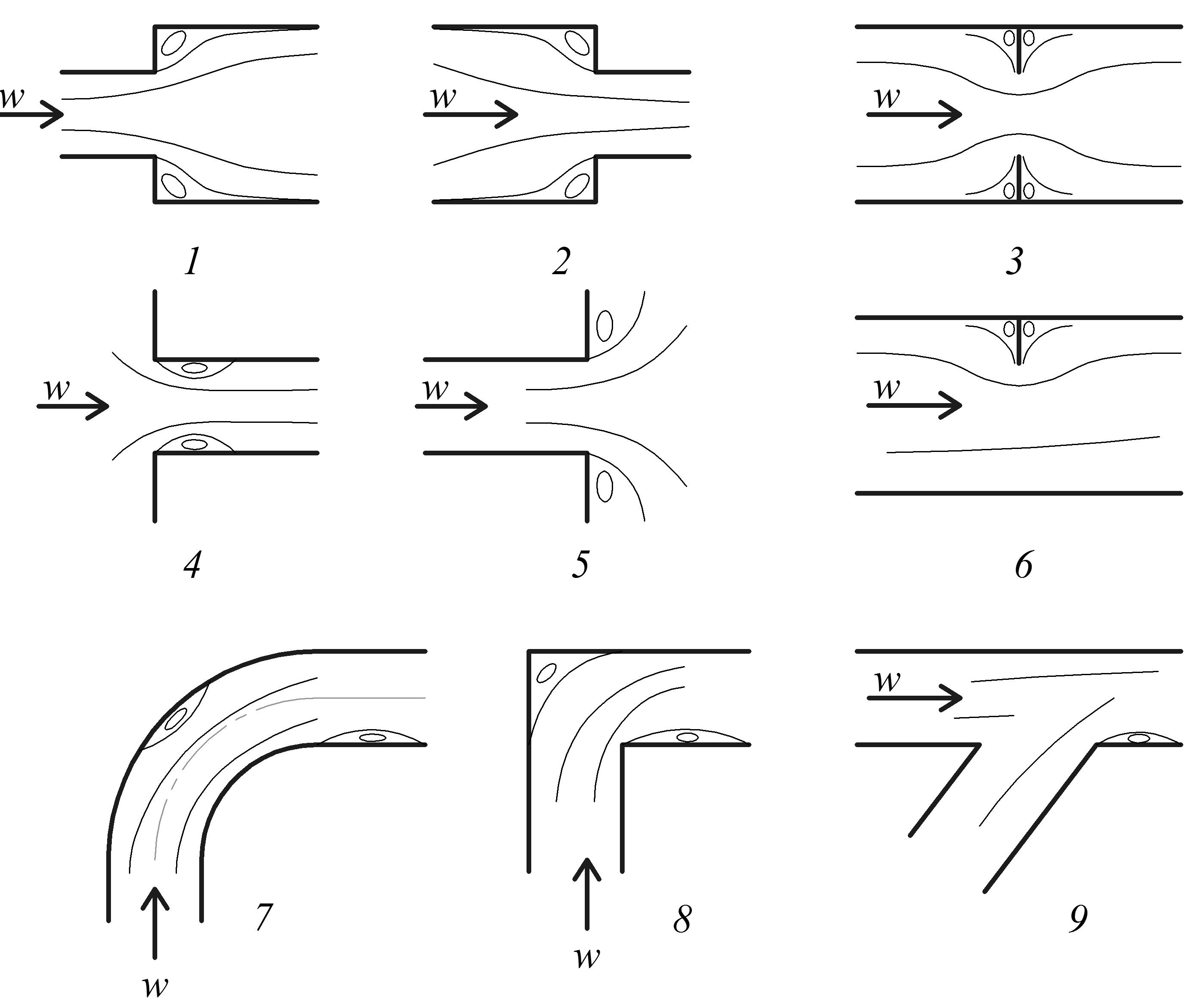
Рис. 2.21. Примеры местных сопротивлений:

1 – расширение; 2 – сужение; 3 – диафрагма; 4 – вход в трубу;

5 – вход в резервуар; 6 – задвижка; 7–8 – повороты; 9 – тройник

Расчетную формулу для местного сопротивления, как формулу Дарси – Вейсбаха, получим из критериального уравнения движения вязкой жидкости:

Как известно, критерий Эйлера определяется как:

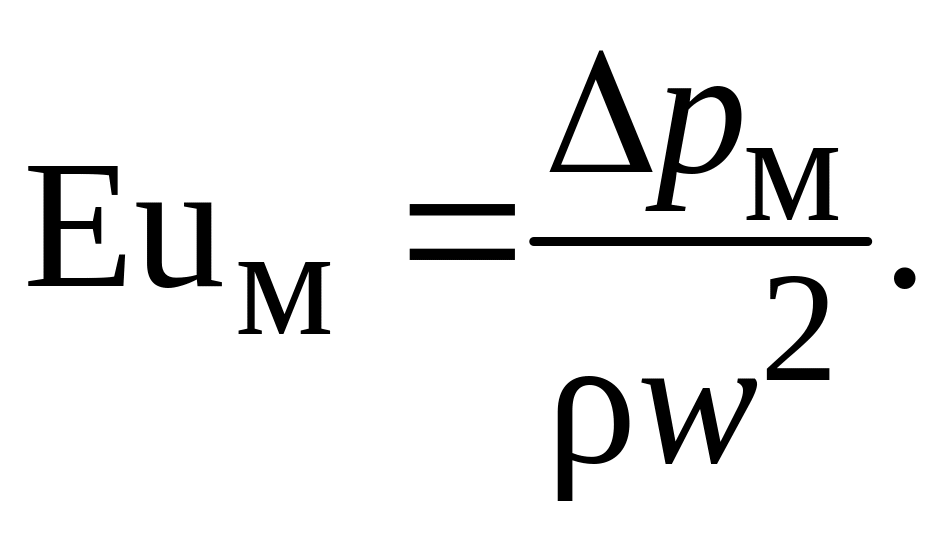
Обозначим неизвестную функции как:

В результате для расчета потери давления на местном сопротивлении получим:

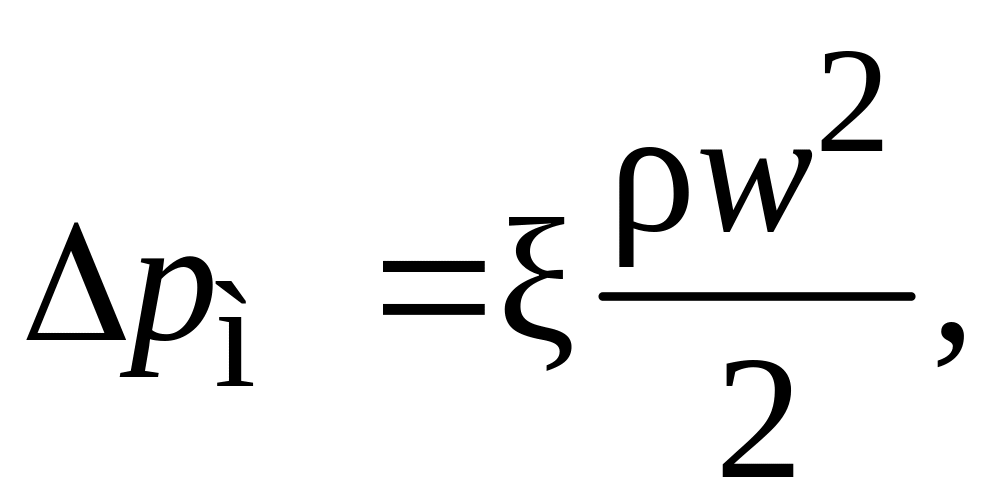(2.60)

Для потери напора можно записать:

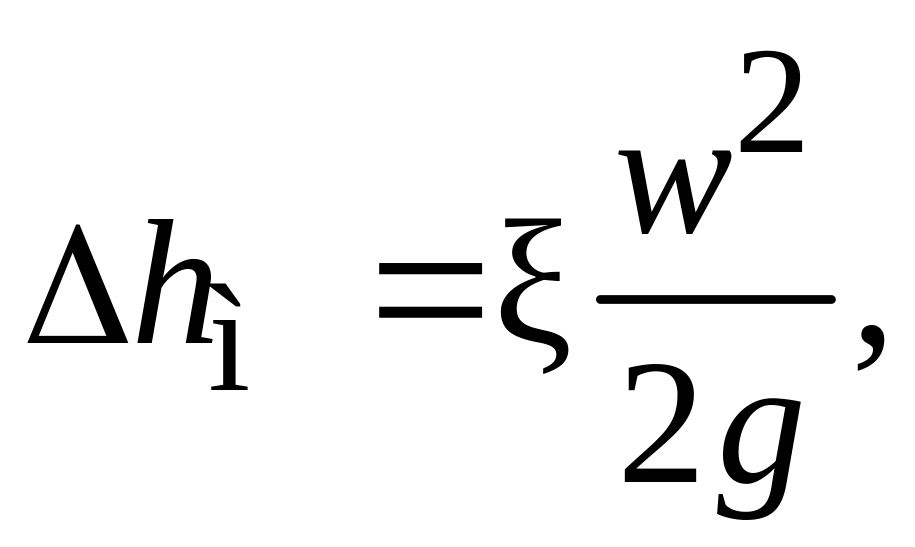
где  – коэффициент местного сопротивления. Коэффициент  показывает, какая часть динамического давления теряется на данном местном сопротивлении или, если , сколько теряется на данном местном сопротивлении.

Рассмотрим  более подробно. В общем случае можно записать:

(2.61)

где – потеря напора, обусловленная вязкостным трением на данном местном сопротивлении, – потери, связанные с отрывом и вихреобразованием. С учетом уравнений Дарси – Вейсбаха и (2.60) можно записать:

или (2.62)

Как показывают экспериментальные исследования, для турбулентного режима первый член правого уравнения вырождается. Поэтому для турбулентного потока принимают . Поскольку в технологических установках в большинстве случаев реализуется турбулентный режим, поэтому в справочниках приводится именно .

Значение  обычно определяют экспериментально, и его значение зависит от конфигурации местного сопротивления. Для одного случая, для внезапного расширения потока, значение  может быть определено теоретическим путем:

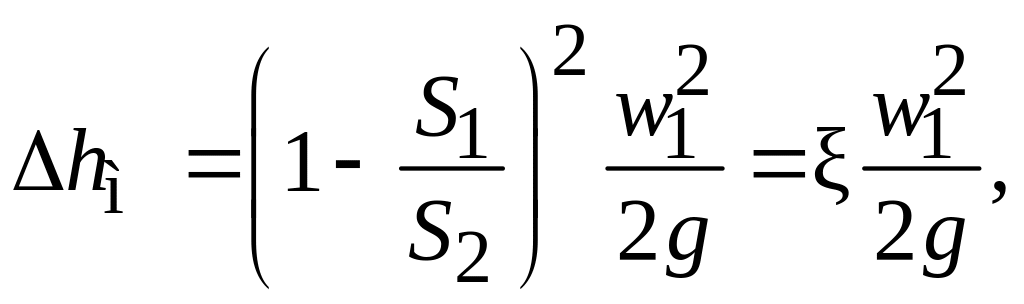(2.63)

где и – соответственно, площадь потока до и после расширения, – скорость потока до расширения. Формула (2.63) называется формулой Бордо.

Интерференция (взаимное влияние) местных сопротивлений. Коэффициент местного сопротивления  определяется из условия, когда к нему подходит стабилизированный поток жидкости. На практике встречаются случаи, когда местные сопротивления устанавливаются друг от друга на весьма малых расстояниях. После каждого местного сопротивления устанавливается свой начальный участок, т.е. изменяются условия подхода потока жидкости к следующему местному сопротивлению. В жидкости не успевает установиться стабилизированное поле скоростей. В этом случае суммарный коэффициент местных сопротивлений существенно будет отличаться от арифметической суммы отдельных, изолированных, коэффициентов местных сопротивлений. В зависимости от расстояния между ними он может быть как значительно больше, так и меньше этой суммы. Итак, можно записать:

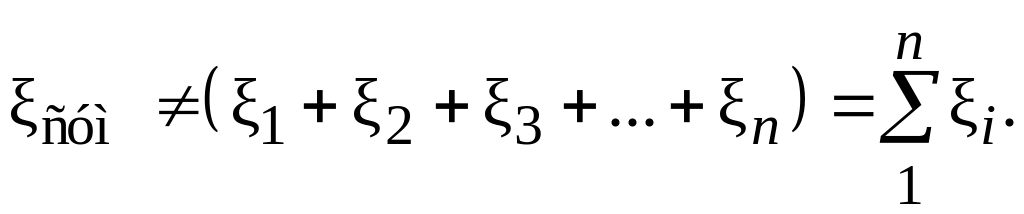(2.64)

Для турбулентного режима течения ориентировочное значение начального участка после местного сопротивления можно оценить как:

Однако конкретных данных по интерференции местных сопротивлений немного.