2.5.2. Турбулентное течение жидкости в трубах

Хаотичное, неупорядоченное движение жидких частиц существенным образом влияет на характеристики турбулентных течений. Эти течения жидкости – неустановившиеся. Благодаря этому в каждой точке пространства скорости изменяются с течением времени. Мгновенное значение скорости можно выразить:

(2.42)

где – осредненная по времени скорость по направлению x, – пульсационная скорость по этому же направлению. Обычно осредненная скорость сохраняет во времени постоянное значение и направление, поэтому такое течение нужно принимать как среднеустановившееся. Когда рассматривается профиль скоростей турбулентного течения для какой-либо области, обычно рассматривают профиль осредненной скорости.

Рассмотрим поведение турбулентного потока жидкости около твердой стенки (рис. 2.17).

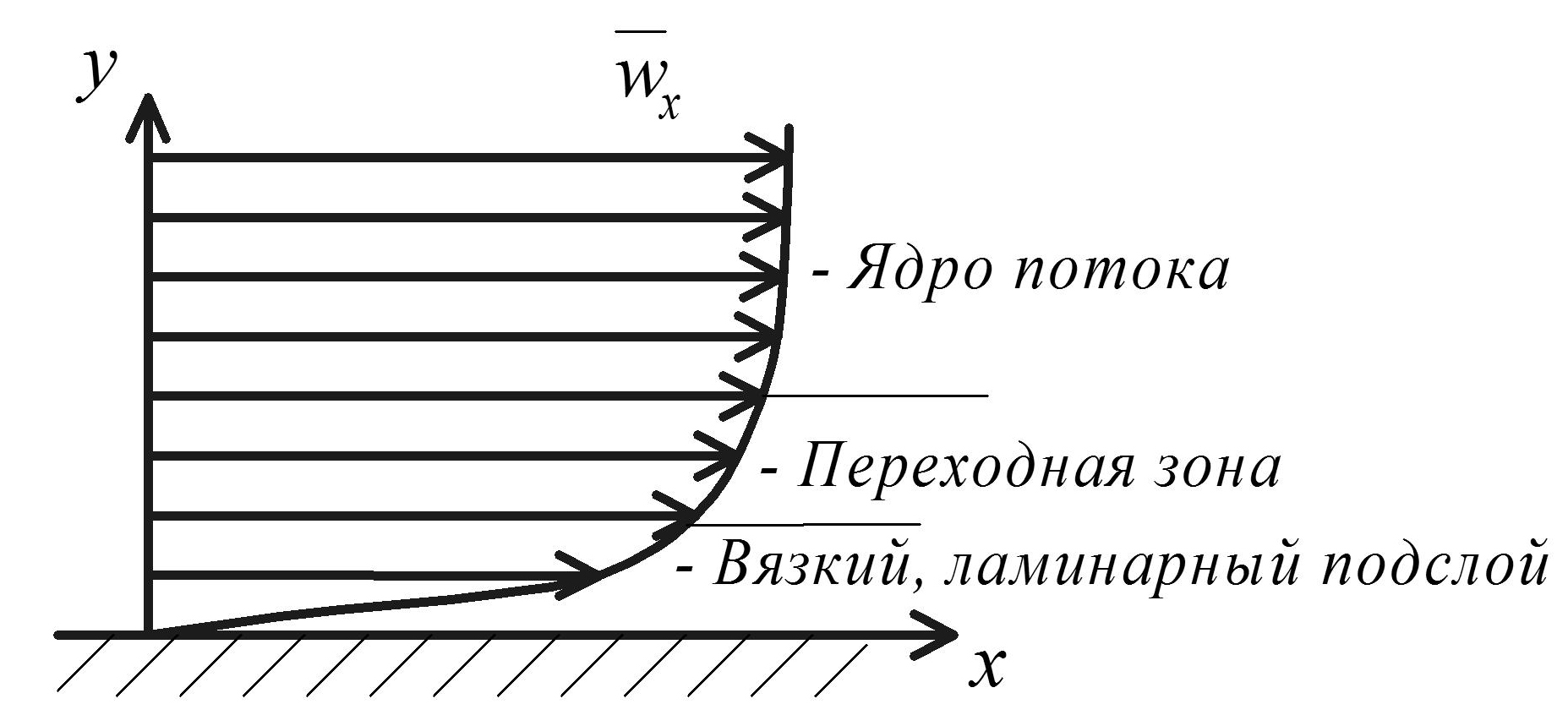
Рис. 2.17. Распределение скорости около твердой стенки

В ядре потока за счет пульсационных скоростей происходит непрерывное перемешивание жидкости. У твердых стенок поперечные движения частиц жидкости невозможны.

Около твердой стенки жидкость течет в ламинарном режиме. Между ламинарным пограничным слоем и ядром потока существует переходная зона.

Движение жидкости при турбулентном режиме всегда сопровождается значительно большей затратой энергии, чем при ламинарном. При ламинарном режиме энергия расходуется на вязкое трение между слоями жидкости; при турбулентном же режиме, помимо этого, значительная часть энергии затрачивается на процесс перемешивания, вызывающий в жидкости дополнительные касательные напряжения.

Для определения напряжения сил трения в турбулентном потоке используется формула:

(2.43)

где – напряжение вязкого течения, – турбулентное напряжение, вызванное перемешиванием. Как известно, определяется законом вязкого трения Ньютона:

_в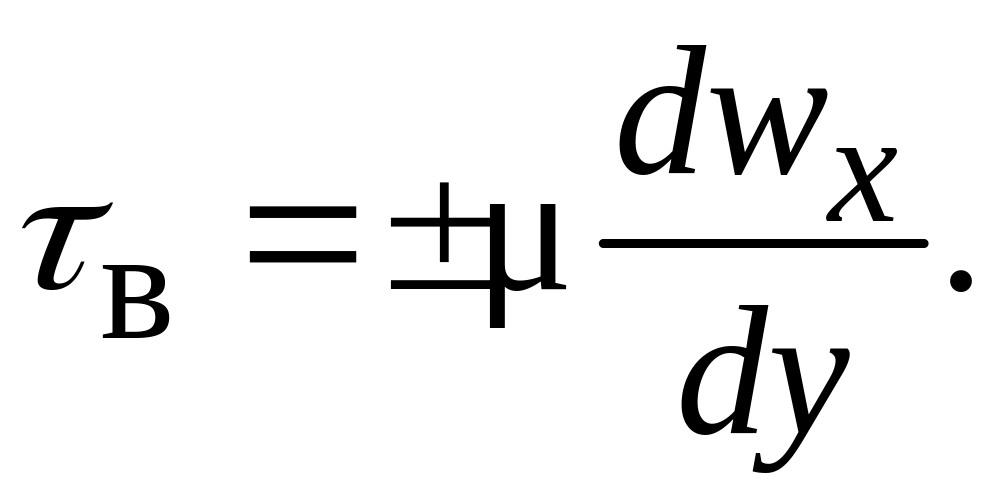

(2.44)

Следуя полуэмпирической теории турбулентности Прандтля, принимая, что величина поперечных пульсаций скорости имеет в среднем один и тот же порядок, что и продольные пульсации, можно записать:

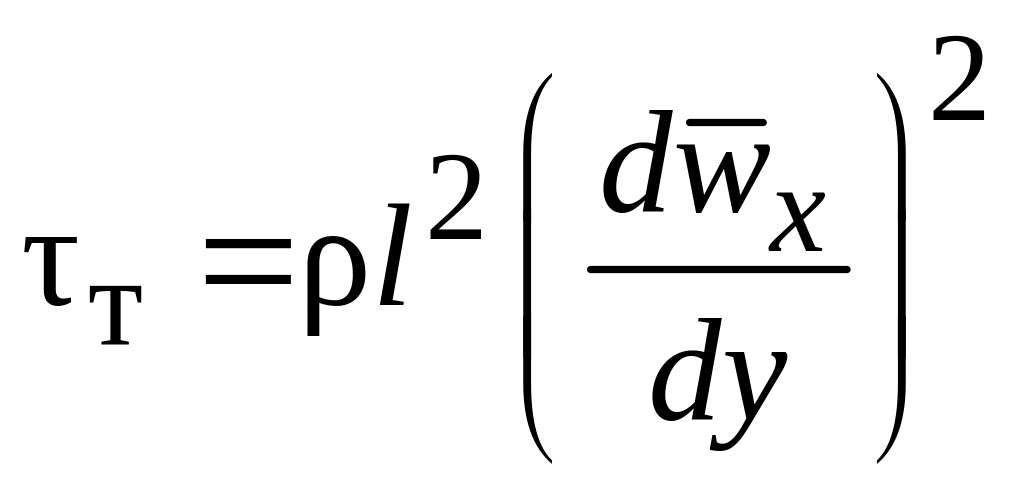. (2.45)

Здесь  – плотность жидкости, l – длина пути перемешивания, – градиент осредненной скорости.

Величина l, характеризующая средний путь пробега частиц жидкости в поперечном направлении, обусловлена турбулентными пульсациями. По гипотезе Прандтля, длина пути перемешивания l пропорциональна расстоянию частицы от стенки:

(2.46)

где  – универсальная постоянная Прандтля.

В турбулентном потоке в трубе толщина гидродинамического пограничного слоя растет значительно быстрее, чем для ламинарного. Это приводит к уменьшению длины начального участка. В инженерной практике обычно принимают:

(2.47)

Поэтому довольно часто влиянием начального участка на гидродинамические характеристики потока пренебрегают.

Далее рассмотрим стабилизированный участок горизонтальной круглой трубы.

Рассмотрим распределение осредненной скорости по сечению трубы. Примем касательное напряжение в турбулентном потоке постоянным и равным напряжению в стенке . Тогда после интегрирования уравнения (2.44) получим:

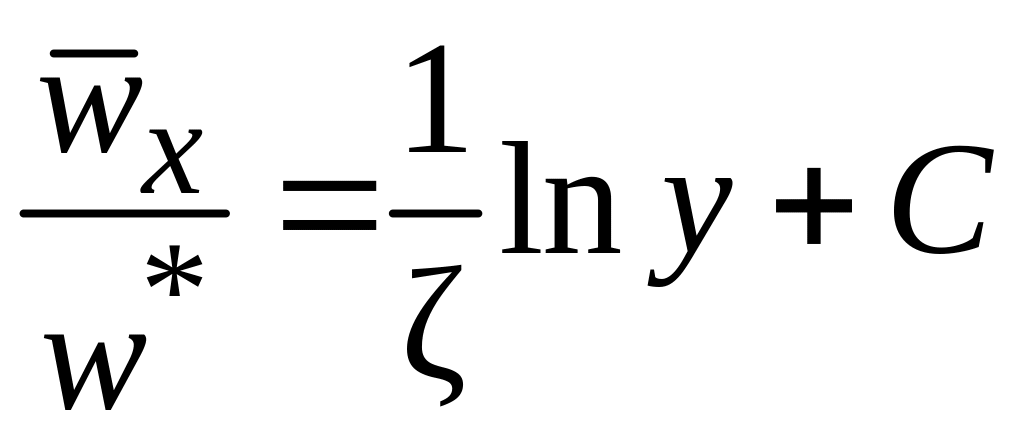. (2.48)

Здесь 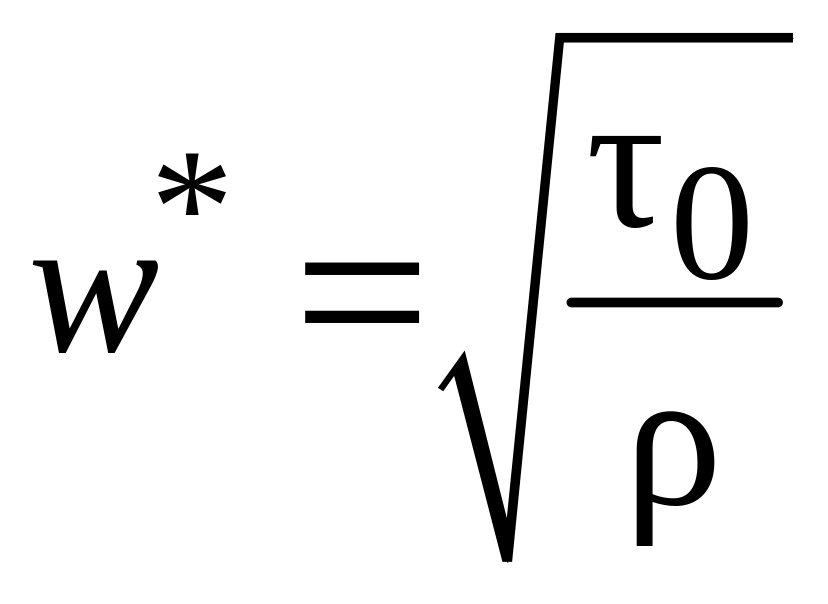– величина, имеющая размерность скорости, поэтому называется динамической скоростью.

Выражение (2.48) представляет собой логарифмический закон распределения осредненных скоростей для ядра турбулентного потока.

Путем несложных преобразований формулу (2.48) можно привести к следующему безразмерному виду:

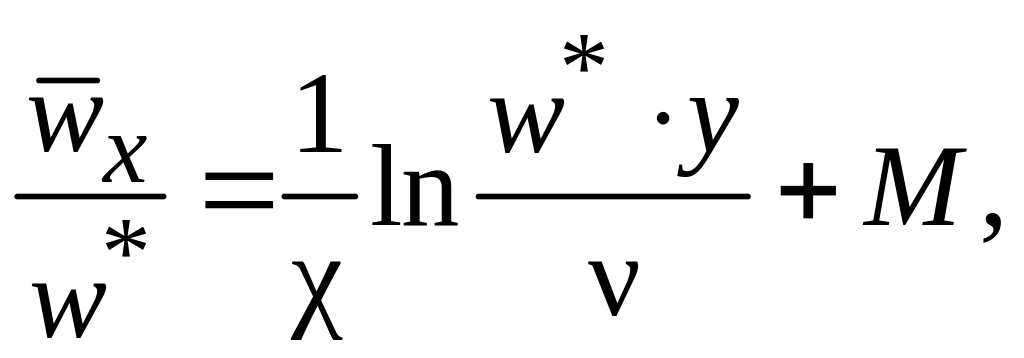(2.49)

где – безразмерное расстояние от стенки; M – константа.

Как показывают опыты,  имеет одинаковое значение для всех случаев турбулентного течения . Значение M было определено опытами Никурадзе: . Итак, имеем:

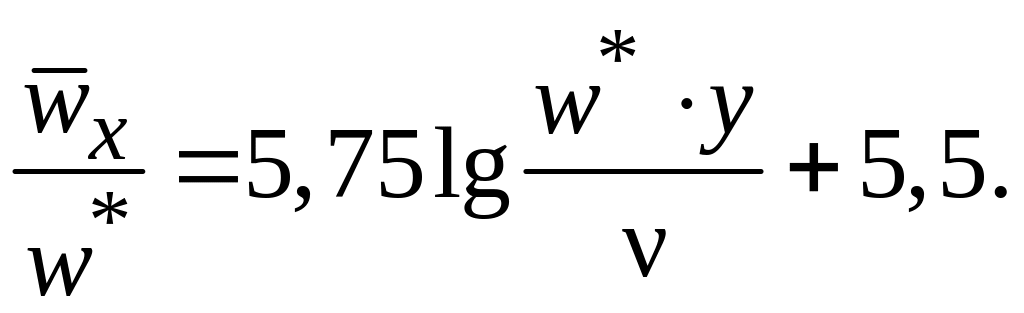(2.50)

В качестве безразмерного параметра, характеризующего толщину соответствующих зон, используется комплекс :

вязкий ламинарный подслой: ,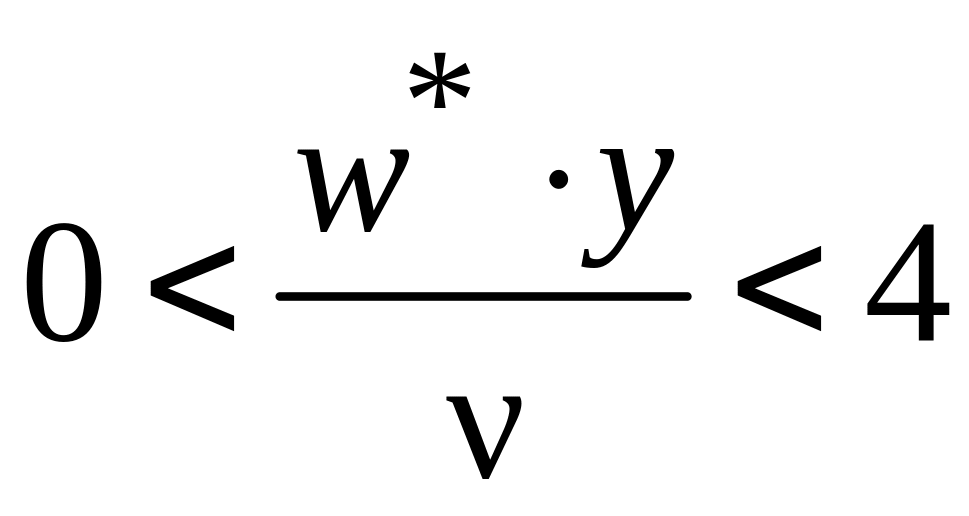

переходная зона: ,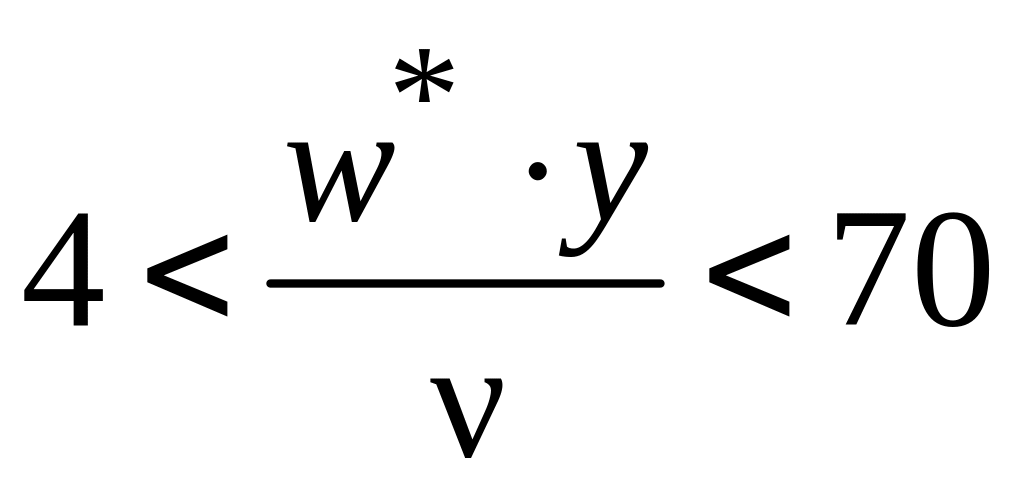

турбулентное ядро: .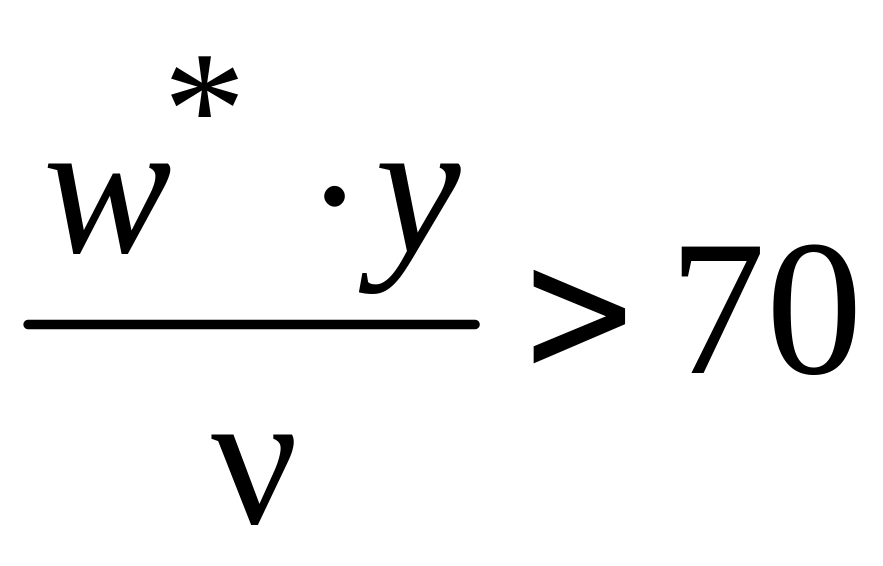

При турбулентом режиме отношение осредненной скорости к максимальной осевой составляет от 0,75 до 0,9.

Зная закон распределения скоростей (рис. 2.18), можно найти величину гидравлических сопротивлений. Однако для определения гидравлических сопротивлений можно использовать более простое соотношение, а именно: критериальное уравнение движения вязкой жидкости, полученное ранее, в первой части дисциплины.

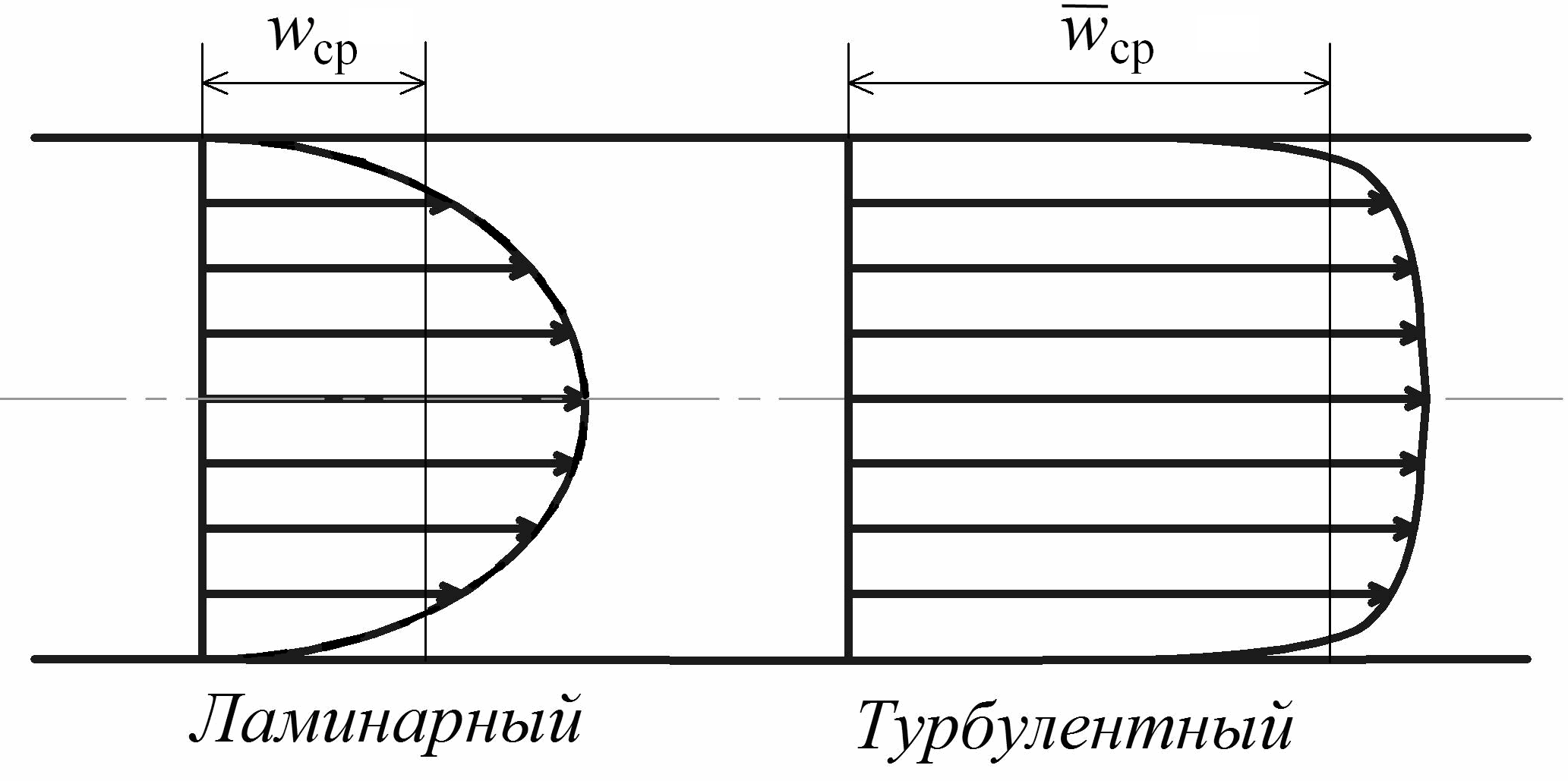
Рис. 2.18. Распределение скоростей в трубе

при ламинарном и турбулентном режимах

Для горизонтальной прямой трубы в случае напорного течения вязкой жидкости критериальное уравнение имеет вид:

(2.51)

где – геометрические комплексы, – критерий Рейнольдса, – критерий Эйлера. Они определяются как:

где ∆ – абсолютная шероховатость трубы, l – длина трубопровода, d – внутренний диаметр трубы. Из опыта известно, что потери давления прямо пропорциональны . Поэтому можно записать:

(2.52)

Далее обозначим неизвестную функцию , распишем критерий Эйлера 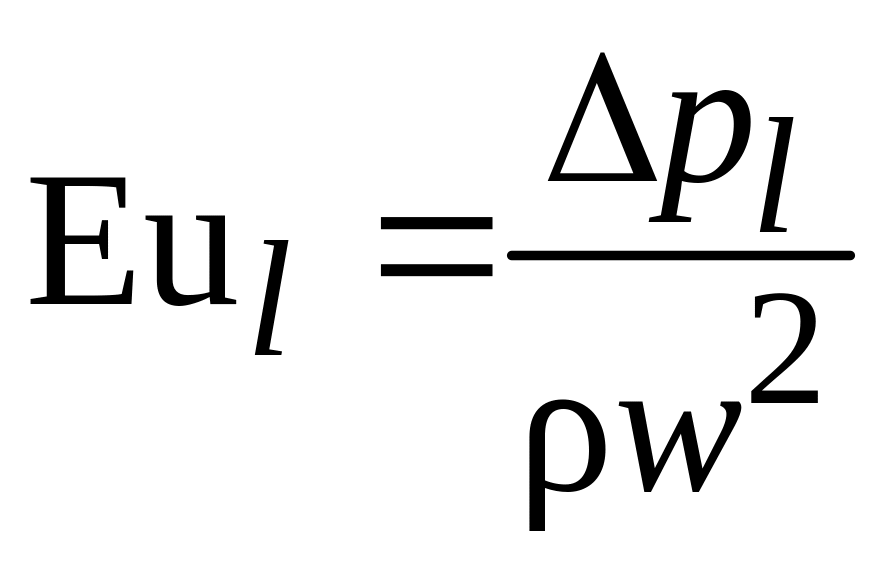. Тогда из уравнения (2.52) для потери давления получим:

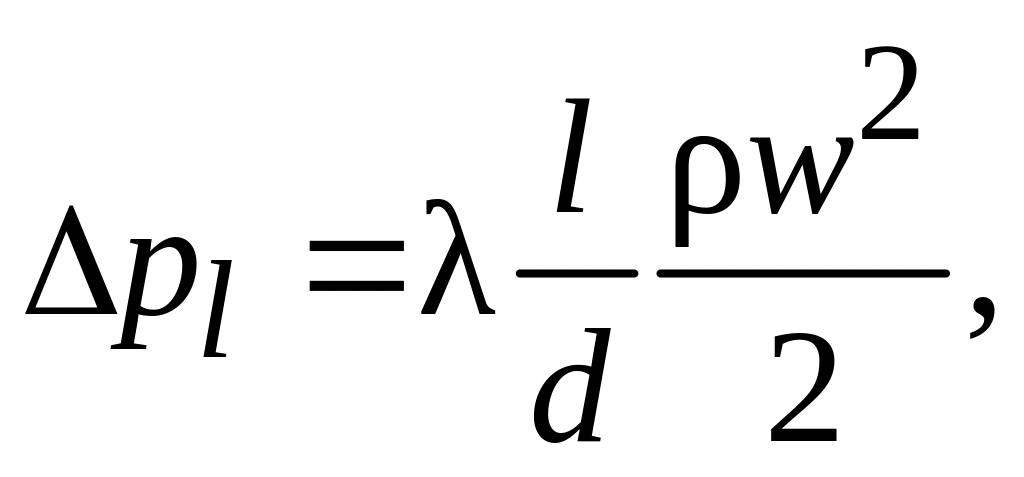(2.53)

где  – коэффициент гидравлического трения, w – средняя скорость потока.

Полученное уравнение носит название уравнение Дарси – Вейсбаха. Уравнение (2.53) может быть представлено в виде потери напора:

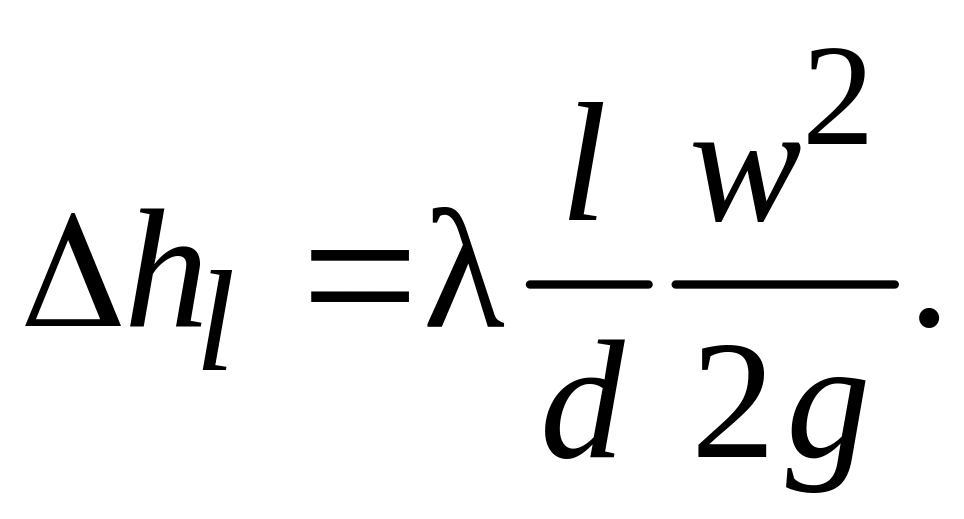(2.54)

Таким образом, расчет потери давления или напора сводится к определению коэффициента гидравлического трения .