- •1.1. Основное уравнение гидростатики
- •1.2. Абсолютное и избыточное давление, вакуум, приборы для их измерения
- •1.3. Закон Паскаля и его использование в технике
- •1.4. Сила давления жидкости на плоские стенки
- •1.5. Сила давления жидкости на криволинейные стенки. Закон Архимеда
- •1.6. Относительный покой жидкости
- •Контрольные вопросы
- •2. Гидравлика
- •2.1. Классификация жидких сред. Реологические среды
- •2.2. Поток жидкости. Геометрические элементы и гидравлические параметры потока
- •2.3. Уравнение Бернулли для элементарной струйки идеальной и вязкой жидкости
- •2.4. Уравнение Бернулли для потока вязкой жидкости. Примеры практического использования уравнения Бернулли
- •2.5. Гидравлическое сопротивление аппаратов и трубопроводов
- •2.5.1. Ламинарное движение жидкости в трубах
- •2.5.2. Турбулентное течение жидкости в трубах
- •2.5.3. График Никурадзе
- •2.5.4. Способы уменьшения гидравлических сопротивлений
- •2.5.5. Местные гидравлические сопротивления. Интерференция местных сопротивлений
- •2.6. Гидравлический расчет трубопроводов, их классификация
- •2.6.1. Расчет простых трубопроводов
- •2.6.2. Расчет сложных трубопроводов
- •2.6.3. Сифонный трубопровод
- •2.7. Особенности расчета газопровода
- •2.8. Некруглые трубопроводы
- •2.9. Определение оптимального диаметра трубопровода
- •2.10. Течение в трубах неньютоновских жидкостей
- •Контрольные вопросы
- •3. Основы динамики двухфазных потоков
- •3.1 Система «жидкость (газ) – твердое тело»
- •3.1.1. Характеристика зернистого слоя
- •3.1.2. Движение жидкости через неподвижный зернистый слой
- •3.1.3. Псевдоожиженный слой
- •3.1.4. Расчет скорости витания (осаждения) и уноса
- •3.1.5. Гидро- и пневмотранспорт зернистых материалов
- •Пневмотранспорт заторможенным плотным слоем
- •3.2. Система «газ (пар) – жидкость»
- •3.2.1. Пленочное течение жидкости
- •3.2.2. Образование и движение капель и газовых пузырей. Барботаж
- •3.3. Система «жидкость – жидкость»
- •Контрольные вопросы
- •4. Разделение неоднородных систем
- •4.1. Классификация неоднородных систем и методов их разделения
- •4.2. Осаждение
- •4.2.1. Разделение неоднородных систем в поле сил тяжести
- •Конструкция аппаратов гравитационного осаждения
- •4.2.2. Разделение неоднородных систем в поле центробежных сил
- •Конструкция аппаратов центробежного осаждения
- •4.2.3. Очистка газов в электрическом поле
- •Конструкции электроосадителей
- •4.3. Мокрая и инерционная очистка газовых неоднородных систем
- •4.4. Фильтрование
- •4.4.1. Основное уравнение фильтрования
- •4.4.2. Фильтрование в поле центробежных сил
- •4.4.3. Аппаратура для фильтрования
- •Очистка газов фильтрованием
- •Фильтрование жидких неоднородных систем
- •4.5. Выбор аппаратов для разделения неоднородных систем
- •Аппараты для очистки газовых неоднородных систем
- •Аппараты для разделения жидких неоднородных систем
- •4.6. Методы повышения эффективности разделения неоднородных систем
- •Контрольные вопросы
- •5. Перемешивание
- •5.1. Перемешивание в жидкой среде
- •5.1.1. Механическое перемешивание
- •Расход мощности на перемешивание
- •5.1.2. Пневматическое перемешивание
- •5.1.3. Гидравлическое перемешивание
- •Контрольные вопросы
- •6. Перемещение жидкостей
- •6.1. Классификация насосов. Элементы насосной установки
- •6.2. Основные рабочие параметры насосов
- •6.3. Лопастные насосы
- •6.3.1. Центробежные насосы
- •Основное уравнение центробежных машин (уравнение Эйлера)
- •Характеристики центробежных насосов
- •Работа центробежного насоса на сеть
- •Параллельная и последовательная работа двух центробежных насосов
- •Высота всасывания центробежных насосов. Кавитация
- •6.3.2. Осевые насосы
- •6.3.3. Вихревые насосы
- •6.4. Поршневые насосы
- •6.4.1. Производительность (подача) поршневых насосов
- •6.4.2. Процессы всасывания и нагнетания поршневых насосов
- •6.4.3. Воздушные колпаки поршневых насосов
- •6.5. Роторные насосы
- •6.5.1. Шестеренные насосы
- •6.5.2. Винтовые насосы
- •6.5.3. Пластинчатые насосы
- •6.5.4. Роторно-поршневые насосы
- •6.6. Характеристики объемных насосов и их работа на сеть
- •6.7. Другие типы насосов
- •6.7.1. Газлифты
- •6.7.2. Монтежю
- •6.7.3. Струйные насосы
- •6.7.4. Гидравлический таран
- •Контрольные вопросы
- •7. Сжатие и перемещение газов
- •7.1. Классификация компрессорных машин
- •7.2. Термодинамические основы сжатия газов
- •7.2.1. Процессы сжатия газа в идеальной компрессорной машине
- •7.2.2. Изотермический и адиабатный кпд компрессорной машины
- •7.3. Поршневые компрессорные машины
- •7.3.1. Производительность и коэффициент подачи
- •7.3.2. Мощность и кпд поршневых компрессорных машин
- •7.3.3. Многоступенчатое сжатие газа в компрессорной машине
- •7.4. Турбокомпрессоры
- •Контрольные вопросы
- •Оглавление
II – часть
Типовые процессы и аппараты
химической технологии
Гидромеханические
процессы и аппараты
1. ГИДРОСТАТИКА
В гидростатике рассматриваются условия (законы) равновесия покоящейся жидкости. Поскольку жидкость находится в состоянии покоя, в ней не проявляются силы вязкого трения. В покоящейся жидкости действуют массовые и поверхностные силы.
В работе [1] из уравнения Навье – Стокса (как частный случай) было получено уравнение равновесия Эйлера:
 (1.1)
(1.1)
Распишем это уравнение по осям в декартовой системе координат:
 (1.2)
(1.2)
где
X,
Y,
Z
– проекции единичных массовых сил по
осям x,
y,
z;
![]() ,
,
![]() ,
,
![]() – градиенты давлений по направлениям
осей x,
y,
z.
– градиенты давлений по направлениям
осей x,
y,
z.
Преобразуем систему уравнений (1.2). Для этого первое уравнение системы (1.2) умножим на dx, второе – на dy, третье – на dz и, сложив эти три уравнения, получим:
 .
.
Правая часть полученного уравнения представляет собой полный дифференциал давления. Следовательно, можно записать:
![]() .
(1.3)
.
(1.3)
Полученное уравнение не содержит частных производных и более удобно для практического использования. Уравнение (1.3) называется основным дифференциальным уравнением гидростатики. Так как dp является полным дифференциалом, а плотность жидкости является постоянной величиной, то выражение в скобках правой части будет также полным дифференциалом некоторой функции координат dU (x, y, z). Эта функция является потенциалом сил. Таким образом, равновесие жидкости возможно, если массовые силы имеют потенциал.
Уравнение (1.3) дает закон распределения давления внутри жидкости при заданной системе сил.
Рассмотрим
поверхность равного давления. Для этого
случая
![]() ,
поскольку
,
поскольку
![]() ,
тогда в качестве общего уравнения
поверхности равного давления в декартовой
системе координат получим:
,
тогда в качестве общего уравнения
поверхности равного давления в декартовой
системе координат получим:
![]() .
(1.4)
.
(1.4)
Некоторые свойства поверхности равного давления:
– две
поверхности уровня не пересекаются
(для одной поверхности
![]() ,
для другой –
,
для другой –
![]() ,
в точке их пересечения было бы
,
в точке их пересечения было бы
![]() ,
а это не так);
,
а это не так);
– внешние массовые силы направлены нормально к поверхности уровня (доказательство от обратного).
Свободная поверхность – поверхность, граничащая с газовой средой – является одной из поверхностей равного давления. Поверхность равного давления относительно Земли представляет собой семейство горизонтальных плоскостей:
![]() ,
т.е.
,
т.е.
![]() .
(1.5)
.
(1.5)
В этом случае из массовых сил действует только сила тяжести.
1.1. Основное уравнение гидростатики
Необходимо получить уравнение, определяющее давление в любой точке покоящейся жидкости (рис. 1.1).
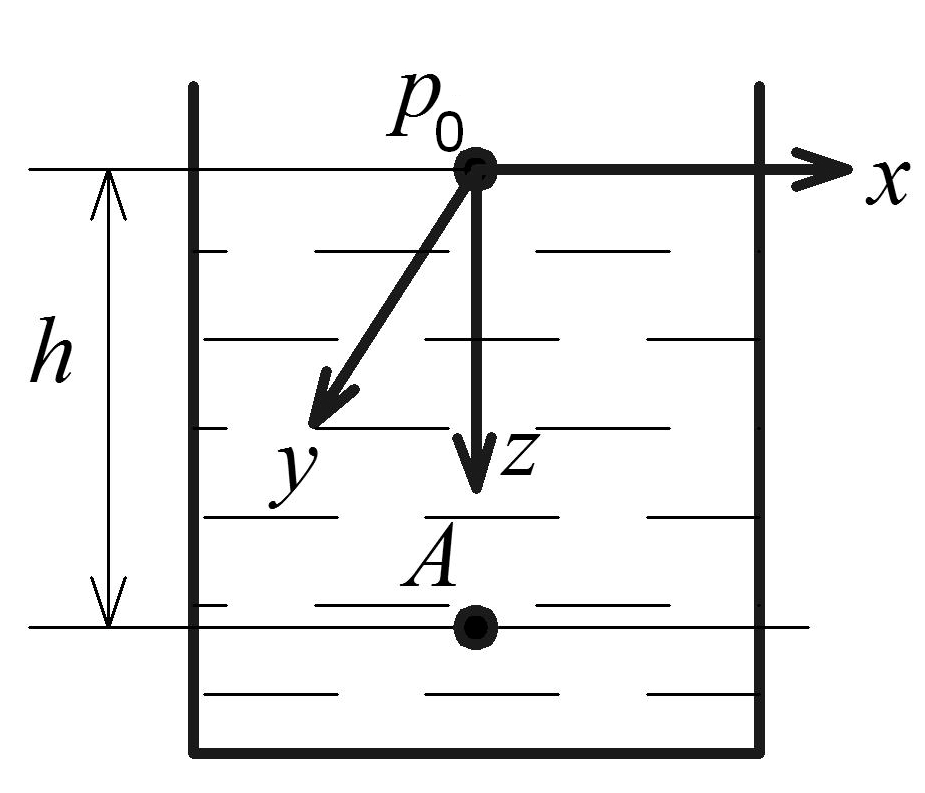
Рис. 1.1. Сосуд, заполненный жидкостью
Основное уравнение гидростатики можно получить разными способами:
– используя уравнение Бернулли, записанное для свободной поверхности и для поверхности, проходящей через точку А;
– используя основное дифференциальное уравнение гидростатики (1.3):
.
В
нашем случае действуют только силы
тяжести. Поэтому
![]() .
Следовательно, имеем:
.
Следовательно, имеем:
![]() .
(1.6)
.
(1.6)
Запишем
граничное условие: при
![]() .
Проинтегрировав уравнение (1.6), получим:
.
Проинтегрировав уравнение (1.6), получим:
![]() .
.
Константа
интегрирования определяется из граничного
условия
![]() .
Итак, имеем:
.
Итак, имеем:
![]() .
.
Для
точки А
при
![]() получим:
получим:
![]() .
(1.7)
.
(1.7)
Полученное
уравнение (1.7) называется основным
уравнением гидростатики. Давление в
точке определяется как сумма давлений
на
свободной поверхности
![]() и давления, создаваемого столбом жидкости
gh.
Величину gh
называют весовым давлением, иногда
давление p
– абсолютным давлением
и давления, создаваемого столбом жидкости
gh.
Величину gh
называют весовым давлением, иногда
давление p
– абсолютным давлением
![]() .
.
Как
видно из формулы (1.7), давление с глубиной
погружения
![]() меняется линейно. Величина
является одинаковой для всей точек
объема жидкости. Следовательно, давление,
приложенное к внешней поверхности
жидкости, передается всем точкам этой
жидкости и по всем направлениям одинаково.
меняется линейно. Величина
является одинаковой для всей точек
объема жидкости. Следовательно, давление,
приложенное к внешней поверхности
жидкости, передается всем точкам этой
жидкости и по всем направлениям одинаково.
1.2. Абсолютное и избыточное давление, вакуум, приборы для их измерения
Различают абсолютное, избыточное давление, вакуум, или разрежение. Если абсолютное давление больше атмосферного, то наблюдается избыточное давление, если меньше – вакуум (вакуумметрическое давление) (рис. 1.2).
Рассмотрим
первый случай:
![]() .
Тогда имеем:
.
Тогда имеем:
![]() .
(1.8)
.
(1.8)
Согласно
формуле (1.8), если давление на свободной
поверхности
![]() ,
то весовое давление
,
то весовое давление
![]() .
.
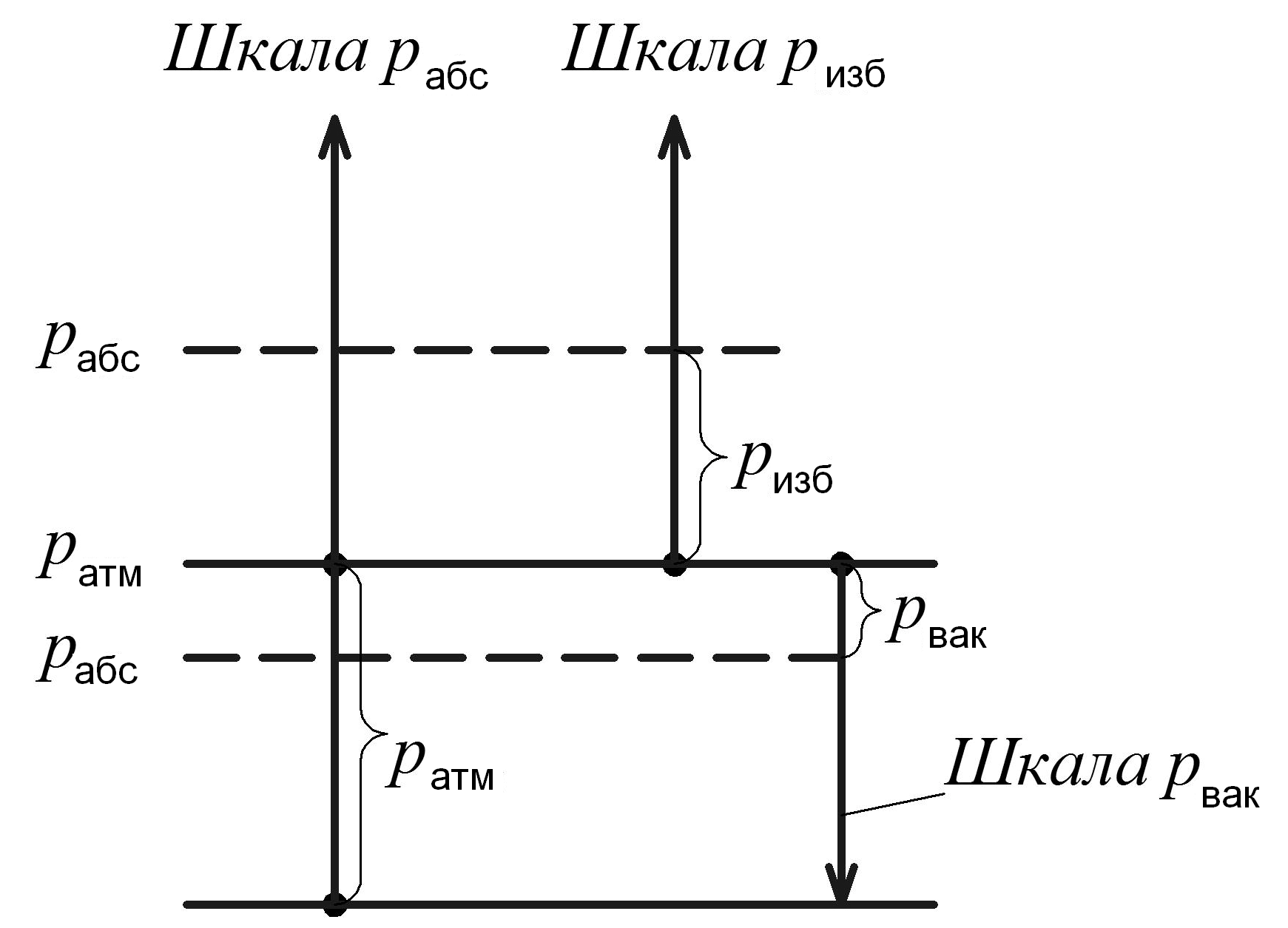
Рис. 1.2. Шкала давлений
Избыточное
давление
![]() бывает и на свободной поверхности.
бывает и на свободной поверхности.
Рассмотрим второй случай:
![]()
Тогда имеем:
![]() .
(1.9)
.
(1.9)
Если давление в жидкости меньше атмосферного, то состояние жидкости характеризуется разрежением (вакуумом). Вакуумметрическое давление (вакуум) определяется из (1.9):
![]() .
(1.10)
.
(1.10)
Шкалы абсолютных и избыточных давлений являются неограниченными, шкала вакуума ограничена – она меняется от атмосферного давления до нуля.
Для измерения гидростатического давления применяются различные приборы. Их можно подразделить на две основные группы: жидкостные и механические.
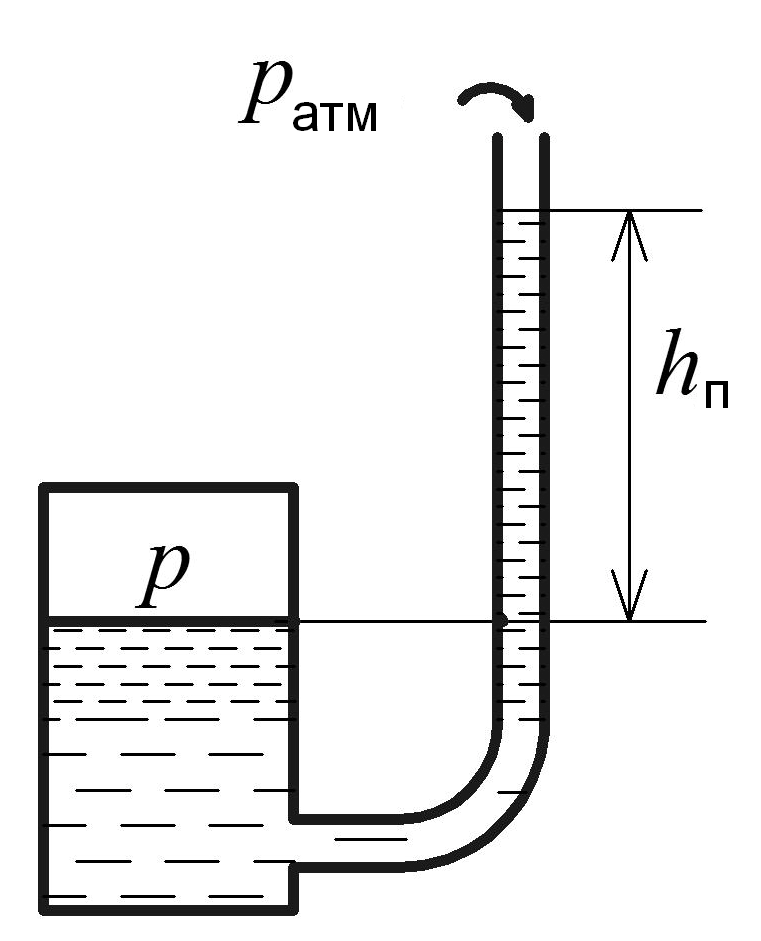
Простейший жидкостной прибор – пьезометр (рис. 1.3). Пьезометр – открытая с обоих концов стеклянная трубка, которая одним концом присоединяется к источнику давления.
Абсолютное давление p определяется по формуле:
![]() ,
(1.11)
,
(1.11)
где
![]() – пьезометрическая высота.
– пьезометрическая высота.
Пьезометры
используют для измерения низких давлений
![]() .
Для измерения высоких давлений применяются
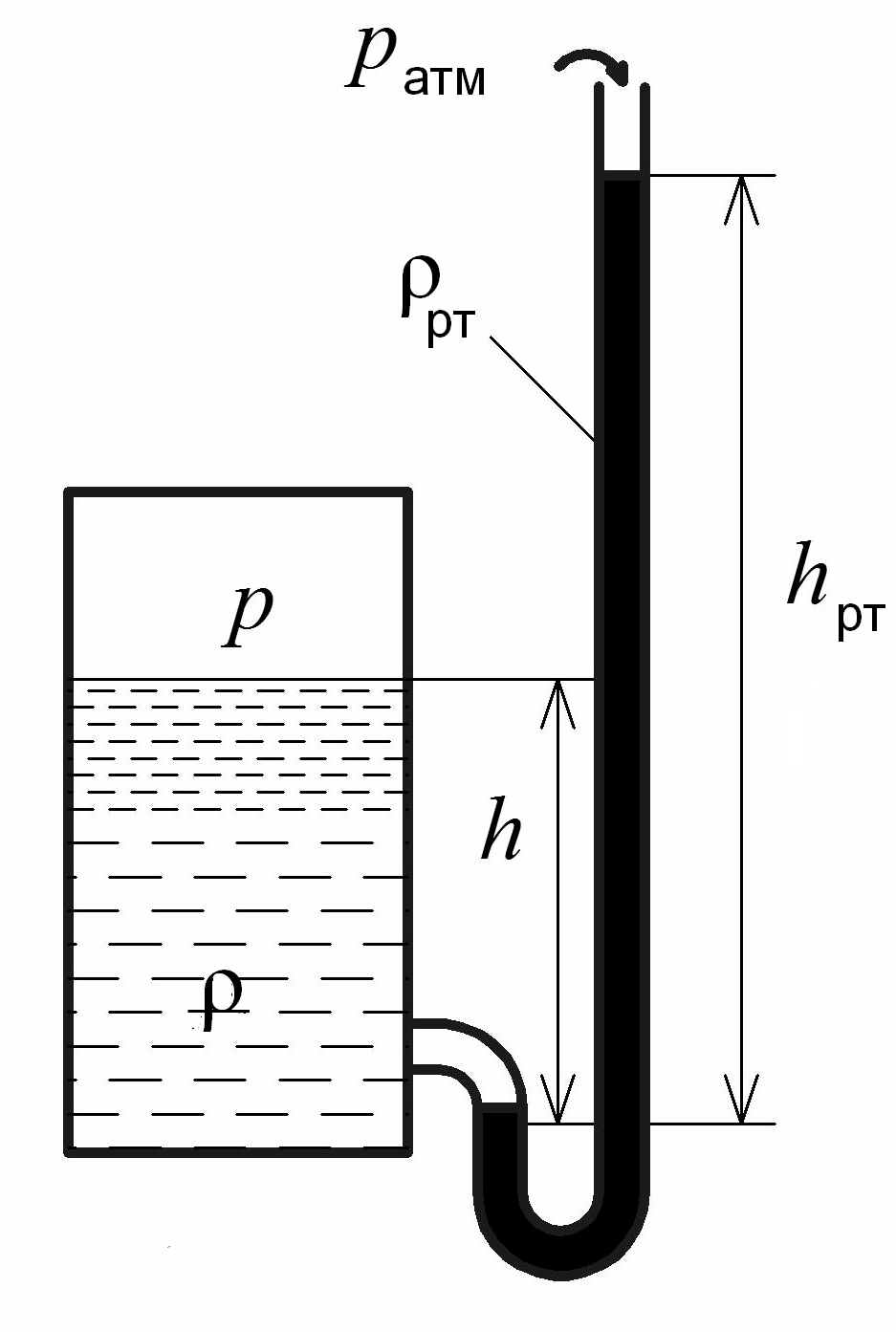
ртутные манометры (рис. 1.4).
.
Для измерения высоких давлений применяются
ртутные манометры (рис. 1.4).
|
|
Рис. 1.3. Пьезометр |
Рис. 1.4. Ртутный манометр |
Абсолютное
давление
![]() измеряется по формуле:
измеряется по формуле:
![]() .
(1.12)
.
(1.12)
Вместо ртути могут быть использованы другие жидкости, плотность которых гораздо выше плотности жидкости, находящейся в резервуаре.
Для измерения перепада давления применяются жидкостные дифференциальные манометры (рис. 1.5).
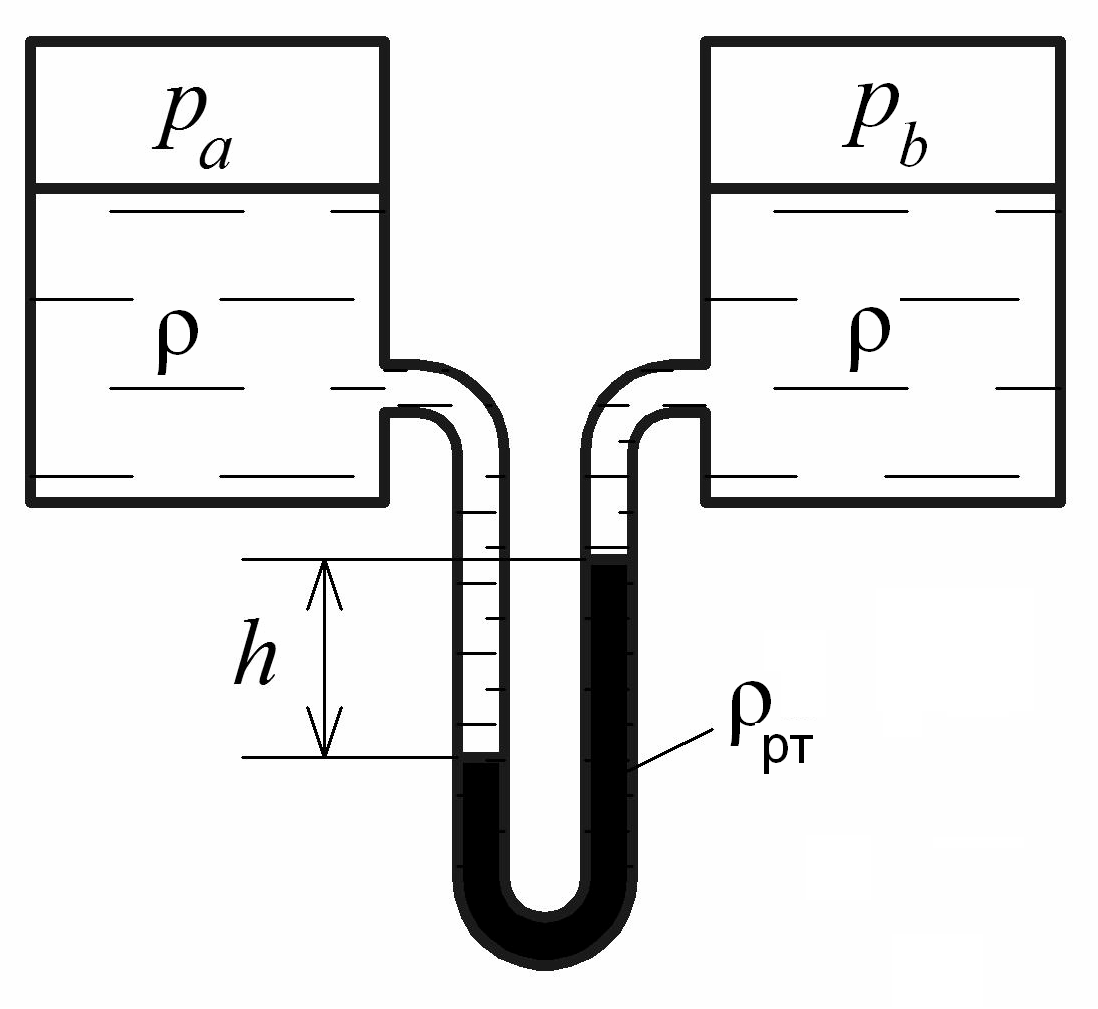
Рис. 1.5. Ртутный дифференциальный манометр
Используется следующая формула для измерения разности давлений:
![]() .
(1.13)
.
(1.13)
Пьезометры могут быть использованы и для измерения вакуума (рис. 1.6). Абсолютное давление в сосуде определяется по формуле:
![]() (1.14)
(1.14)
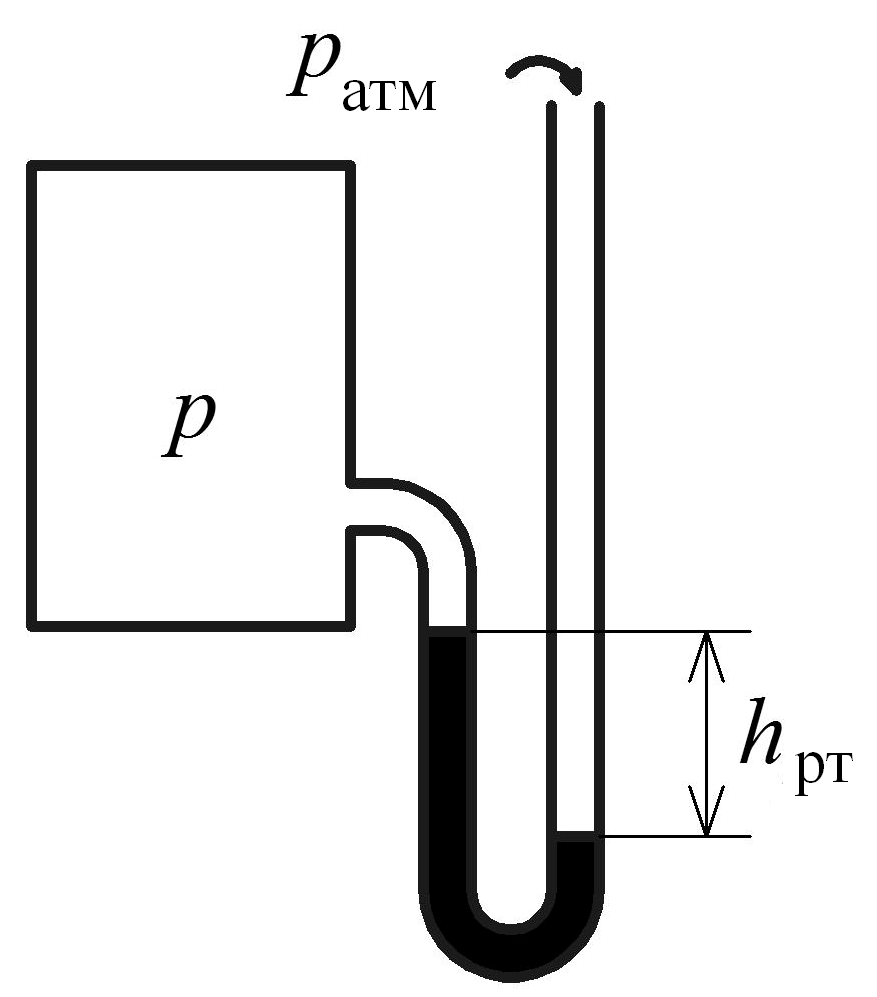
Рис. 1.6. Измерение вакуума
Следовательно:
 (1.15)
(1.15)
Обычно
![]() называют вакуумметрической высотой и
обозначают
называют вакуумметрической высотой и
обозначают
![]()
Жидкостные манометры просты по конструкции, характеризуются большой точностью измерений, однако они применяются для измерения сравнительно небольших давлений. Для измерения больших давлений применяются механические манометры. В механических манометрах жидкость измеряется величиной деформации гибкого элемента (полой пружины, мембраны). Механические манометры могут применяться и для измерения малых давлений и вакуума (моновакуумметры). Широкое распространение нашли сильфонные перепадомеры, дифференциальные сильфонные манометры.