1.2. Прямоугольная декартова система координат на плоскости.

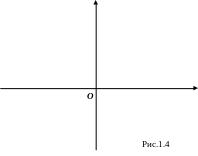
1.2.1. Введём две перпендикулярные прямые и введём на каждой из них системы координат, взяв за начало на каждой из них их точку пересечения О и взяв на каждой из них один и тот же масштаб (то есть величина единичного отрезка на каждой оси одинакова). Как правило, одна ось берётся горизонтальной с направлением слева направо, а другая  вертикально с направлением снизу вверх (рис. 1.4).

Г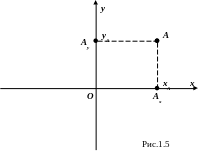 оризонтальную ось обозначим через Ox и назовём её осью абсцис, вертикальную  через Oy и назовём её осью ординат. Оси также называются координатными осями. Пара (Ox, Oу) называется прямоугольной декартовой системой координат на плоскости.

Возьмём на плоскости произвольную точку А и опустим из неё перпендикуляры на оси Ox и Oy. Основания перпендикуляров обозначим через A_x и A_y соответственно. Они имеют на осях какие-то координаты, скажем, x_A и y_A. Таким образом, A_x(x_A) и A_y(y_A)  основания перпендикуляров точки А на осях (рис. 1.5).

Пара (x_A, y_A) называется координатами точки А, при этом x_A  абсцисса точки А, y_A  ордината точки А. Тот факт, что точка А имеет координаты (x_A, y_A), обозначается через А(x_A, y_A).

1.2.2. Теорема. Если точки A(x_A, y_A) и B(x_B, y_B) заданы своими координатами, то расстояние между ними равно

|АВ|= ,

и если точка C(x_C, y_C) делит отрезок АВ в отношении , то x_C= , y_C= .

1.2.3. Упражнения.

1) Даны точки A и B своими координатами. Известно, что точка C делит отрезок AB в отношении . Найти длину отрезка AB и координаты точки C. На координатной плоскости отметить точки A, B и С:

а) A(2; 3), B(4; 2), = ;

б) A(3; 2), B(4; 2), = ;

в) A(2; 4), B(4; 2), = .

Решение. а) По теореме 1.2.2 имеем

|АВ|= = = .

По той же теореме

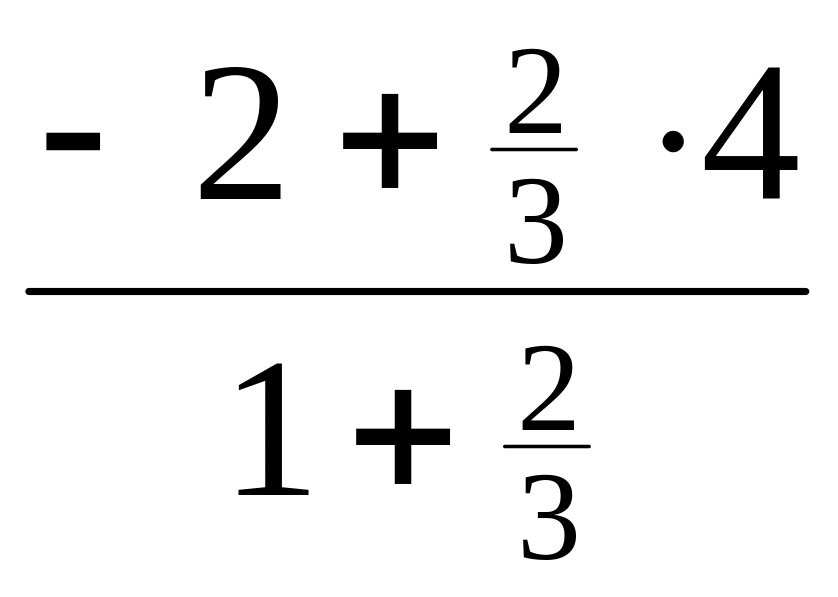x_C= = = , y_C= = = ,

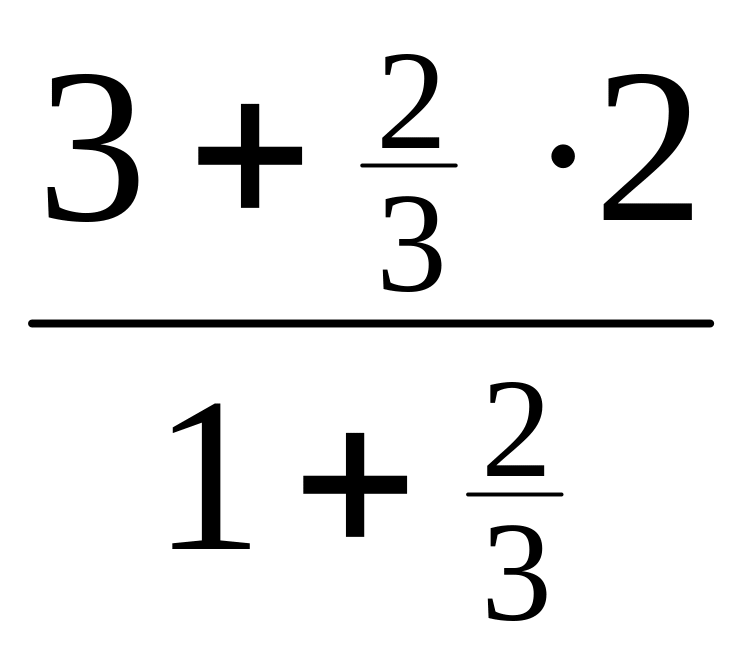то есть  координаты точки С.

На координатной плоскости отметим точки A, B и С:

Ответ: Длина отрезка АВ равна , координаты точки C равны .

2) Даны вершины треугольника АВС. Найти длины сторон треугольника и координаты точки пересечения медиан. Сделать чертёж:

а) A(2; 3), B(3; 1), С(5; 4);

б) A(3; 2), B(4; 2), С(4; 3);

в) A(2; 4), B(4; 2), С(2; 3).

Решение. а) По теореме 1.2.2 имеем

|АВ|= = = ,

|АС|= = = ,

|BС|= = = .

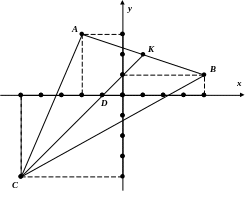
Медианы треугольника пересекаются в одной точке D и делятся в отношении =2, если считать от вершины треугольника (то есть если медиана опущена из вершины C к середине K противолежащей стороны AB, то =2). Найдём координаты точки K:

x_K= = =1, y_K= = =2,

то есть (1; 2)  координаты точки K.

Теперь можем найти координаты точки пересечения медиан:

x_D= = = 1, y_D= = =0,

то есть (1; 0)  координаты точки D.

Ответ: а) Длины сторон треугольника: |АВ|= , |АС|= , |BС|= . D(1; 0)  точка пересечения медиан.

1.3. Прямоугольная декартова система координат в пространстве

1.3.1. Введём три взаимно перпендикулярные прямые, пересекающиеся в одной точке, и введём на каждой из них системы координат, взяв за начало на каждой из них их общую точку пересечения О и взяв на каждой из них один и тот же масштаб. Как правило, одна ось берётся вертикальной с направлением снизу вверх, а другие две  на горизонтальной плоскости с направлениями так, как это показано на рис. 1.7.

Горизонтальные оси обозначим через Ox, Оу (так, как это изображено на рис. 1.8) и назовём их соответственно осями абсциис и ординат, а вертикальную  через Oz и назовём её осью аппликат. Плоскости, содержащие пары координатных осей, называются координатными плоскостями. Они обозначаются в соответствии с тем, какие оси содержат: xOy, xOz, yOz. Тройка (Ox, Oу, Oz) называется прямоугольной декартовой системой координат в пространстве.

Возьмём в пространстве произвольную точку А и проведём через неё плоскости, перпендикулярные к осям Ox, Oy и Oz. Эти плоскости пересекают оси в некоторых точках. Обозначим их соответственно через A_x, A_y и A_z. Они имеют на осях какие-то координаты, скажем, x_A, y_A и z_A. Таким образом, A_x(x_A), A_y(y_A) и A_z(z_A)  основания перпендикулярных к осям плоскостей, проведённых из точки А (рис. 1.9).

Тройка чисел (x_A, y_A, z_A) называется координатами точки А, при этом x_A  абсцисса точки А, y_A  ордината точки А, z_A  аппликата точки А. Тот факт, что точка А имеет координаты (x_A, y_A, z_A), обозначается через А(x_A, y_A, z_A).

П ри изображении положения точки А(x_A, y_A, z_A) относительно своих координат проводят проекцию A точки A на координатную плоскость xOy, затем проводят отрезки AA_x, AA_y, параллельные соответственно осям Oy, Ox, и отрезок AA_z, параллельный отрезку AO (рис.1.10, здесь точки A_x, A_y, A_z обозначены их координатами, соответственно через x_A, y_A, z_A).

1.3.2. Теорема. Если точки A(x_A, y_A, z_A) и B(x_B, y_B, z_B) заданы своими координатами, то расстояние между ними равно

|АВ|= ,

и если точка C(x_C, y_C, z_C) делит отрезок АВ в отношении , то x_C= , y_C= , z_C= .

1.3.3. Упражнение. Даны точки A и B своими координатами. Известно, что точка C делит отрезок AB в отношении . Найти длину отрезка AB и координаты точки C. В системе координат изобразить отрезок AB:

а) A(2; 3; 4), B(4; 2; 3), = ;

б) A(3; 2; 1), B(4; 2; 0), = ;

в) A(2; 4; 3), B(4; 2; 2), =3.

Решение. а) По теореме 1.3.2 имеем

|АВ|= = = ,

По той же теореме

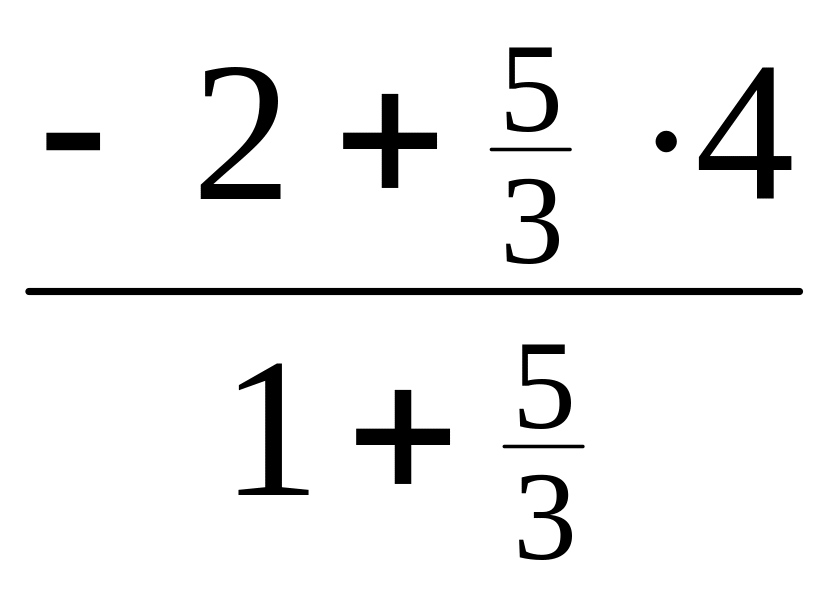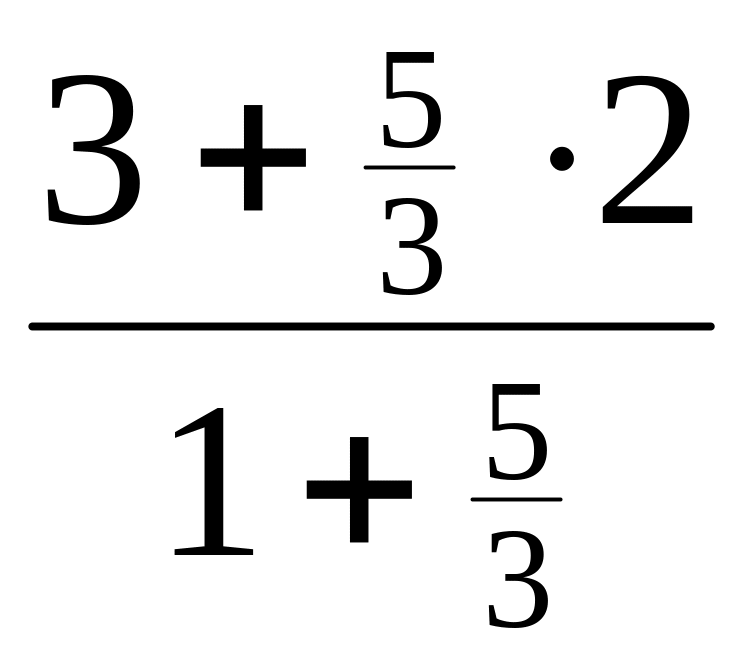x_C= = = , y_C= = = , z_C= = = 

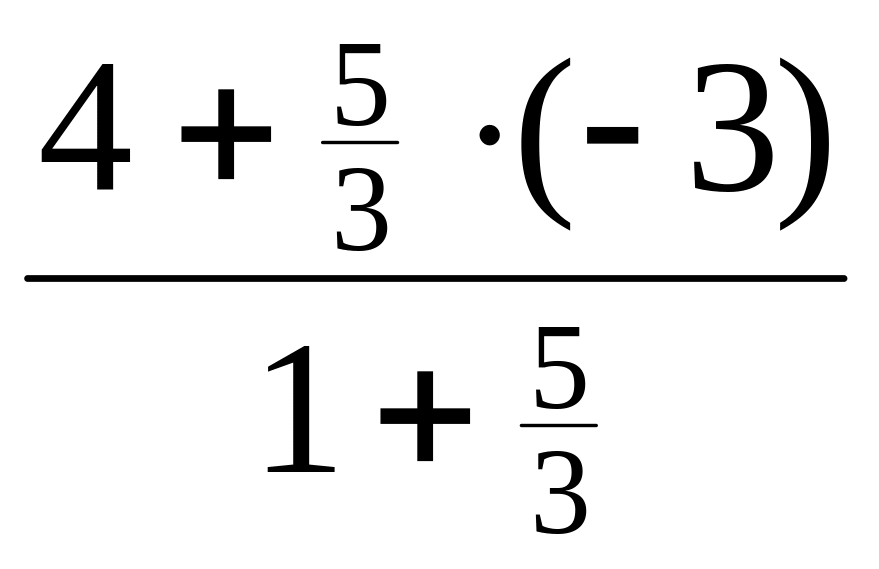то есть  координаты точки С.

В системе координат изобразим отрезок AB:

Ответ: |АВ|= ,  координаты точки С.