3.2. Векторное произведение векторов и его свойства.
3.2.1. Векторным произведением векторов и называется вектор , обладающий следующими свойствами:
1) , ;
2) | |=| || |sin( );
3) тройка ( , , ) правая.
Векторное произведение векторов и обозначается через [ , ] и .
3.2.2.
Свойство 3) определения векторного
произведения векторов
и
выражает его геометрический смысл:
Геометрический
смысл векторного п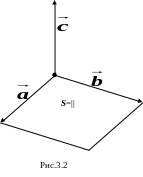
роизведения
заключается в том,
что длина
векторного произведения равна площади
параллелограмма,
натянутого
на сомножители
(рис.3.2).
При этом и коллинеарны, тогда и только тогда, когда [ , ]= .
3.1.3. Теорема. Векторное произведение векторов обладает следующими свойствами:
1о. Для любых векторов и имеет место равенство
[ , ]=[ , ].
2о. Для любого числа и любых векторов и имеют место равенства
[ , ]=[ , ],
[ , ]=[ , ].
3о. Для любых векторов , и имеют место равенства
[ + , ]=[ , ]+[ , ],
[ , + ]=[ , ]+[ , ].
4о. Если =(ax, ay, az), =(bx, by, bz), то
[
,
]=
,
,
(3.4)
или, в виде разложения в системе орт
[
,
]=
+
(3.5)
3.2.4. Свойства 2о и 3о обобщаются на любое число слагаемых в любом из сомножителей:
[1 +2 +…+k , ]=1[ , ]+2[ , ]+…+k[ , ],
[ , 1 +2 +…+k [=1[ , ]+2[ , ]+…+k[ , ]
Аналогичное обобщение имеет место на любое число слагаемых в обоих сомножителях. Например,
[ + , + + ]=
= [ , ]+[ , ]+[ , ]+[ , ]+[ , ]+[ , ].
3.2.5. Равенство (3.5) формально записывается в виде
[
,
]=
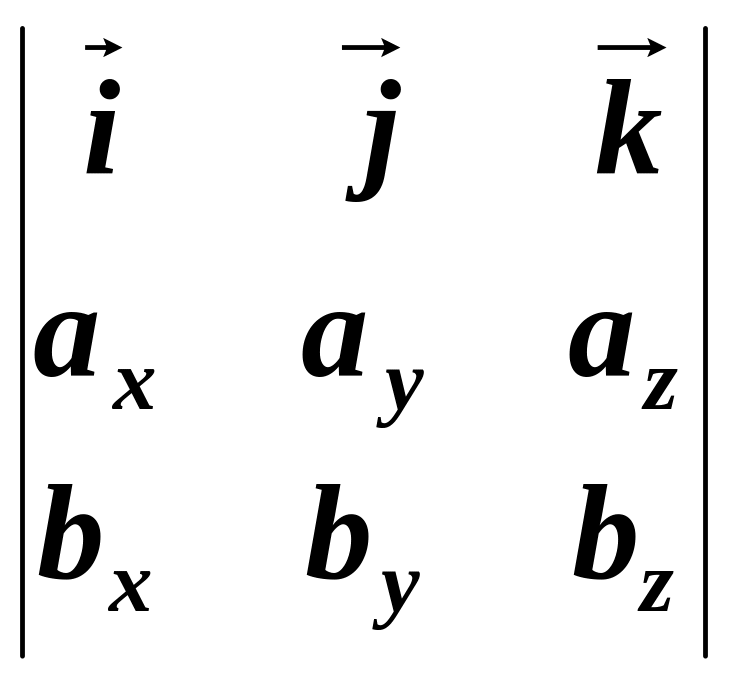(3.6)
Формула (3.6) позволяет легко восстановить формулу (3.5) (при условии знания определителя 3-го порядка или его разложения по первой строке).
3.2.6. Упражнения.
1) Вычислить площадь параллелограмма, построенного на векторах и , если:
а)
=2
3
,
=
+3
,
|
|=2,
|
|=3,
(
)=
;
б) =2 4 , =3 2 , | |=1, | |=4, ( )= ;
в) = +5 , =2 , | |=2, | |=4, ( )= .
Решение. а) В силу геометрического смысла векторного произведения (3.2.2) площадь S параллелограмма, натянутого на векторы и , равна длине вектора [ , ], то есть S=|[ , ]|. Найдём отдельно [ , ]:
[
,
]=[2
3
,
+3
]
2[
,
]+3[
,
]+6[
,
]9[
,
]
3[ , ]+6[ , ]=3[ , ].
Поэтому S=|3[ , ]|=3|[ , ]|=3| || |sin( )=323sin =9 .
(1) Воспользовались обобщением 3.2.4 свойств векторного произведения.
(2) Воспользовались
свойствами [
,
]
и [
,
]=[
,
]
Ответ: а) S=9 .
2) Найти векторное произведение векторов и и его длину:
а) =(3; 2; 4), =(2; 1; 3);
б) =(1; 2; 4), =(3; 5; 1);
в) векторы и из упр 1.а), =(1; 1; 3), =(4; 2; 5);
г) =3 + , =4 2 , =(2; 0; 1), =(2; 3; 6).
Решение. а) По формуле (3.5) имеем
[
,
]=
+
=2
+
,
То
есть [
,
]=2
+
.
Далее |[
,
]|=
=
.
в) [ , ]=[2 3 , +3 ]=3[ , ] (см. решение упр. 1.а)) Далее,
[
,
]=
+
=5
+7
+2
.
Отсюда
[
,
]=3(5
+7
+2
)=15
+21
+6
и |[
,
]|=
=
.
Ответ: а) [ , ]=2 + , |[ , ]|= ;
в) [ , ]=15 +21 +6 , |[ , ]|= .