1.2. Сложение векторов.

1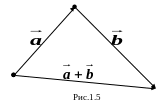 .2.1. Суммой векторов и называется вектор, начало которого совпадает с началом , а конец  с концом , при условии, что начало приложено к концу . Обозначается сумма и через + (рис.1.5).

1.2.2. Теорема. Сумма векторов обладает следующими свойствами:

1^о. Для любых векторов и

+ = + .

2^о. Для любых векторов , и

( + )+ = +( + ).

3^о. Существует такой вектор , что для любого вектора

+ = .

4^о. Для любого вектора существует вектор такой, что

+ = .

Прокомментируем перечисленные свойства.

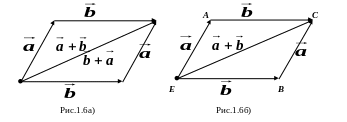
1^о. Равенство векторов + и + усматривается из простых геометрических соображений, приведённых на рис.1.6а).

Из этого свойства легко усматривается правило построения суммы векторов и : Для получения суммы + достаточно отложить векторы и из одной точки, построить параллелограмм EACB, где = , = . Тогда = + (рис.1.6б)). При этом говорят, что параллелограмм EACB построен на векторах и .

2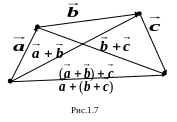 ^о. Равенство векторов ( + )+ и +( + ) также усматривается из геометрических соображений (рис.1.7).

3^о. Ясно, что роль играет : + = .

4^о. В этом свойстве утверждается, что для любого вектора существует противоположный  : если = , то = = и + = = .

1.3. Умножение вектора на число.

1.3.1. Произведением (умножением) вектора на число  называется такой вектор , что:

1) | |=||| |;

2) Если >0, то , а если <0, то (если =0, то из условия 1) вытекает, что | |=0, то есть = ).

Например, на рис.1.8 изображены векторы , 3 и .

1.3.2. Теорема. Произведение вектора на число обладает следующими свойствами:

1^о. Для любого вектора

1 = .

2^о. Для любых чисел ,  и любого вектора

 ( )=() .

3^о. Для любых чисел ,  и любого вектора

(+) = + .

4^о. Для любых числа  и векторов и

( + )= + .

§2. Множество векторов как линейное пространство

2.1. Множество векторов как линейное пространство

2.1.1. Теорема. Множество векторов на плоскости (в пространстве) образует линейное пространство.

Это вытекает из определения суммы векторов и произведения вектора на число, и из свойств этих операций. А именно, Теорема 1.2.2 даёт свойства 1^о  4^о определения линейного пространства, а Теорема 1.3.2  свойства 5^о  8^о определения. Причём можно рассматривать (как линейное пространство) отдельно векторы на плоскости и отдельно в пространстве.

Из теоремы 2.1.1 вытекает, что для векторов (как на плоскости, так и в пространстве) выполнены все свойства линейного пространства (рассмотренные в главе I). Перечислим некоторые из них применительно к векторам:

1. Нулевой нулевой вектор единствен.

2. Для любого вектора его противоположный вектор  единствен.

3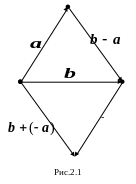 . Сумма вида (...(( + )+ )+...)+ не зависит от расстановки скобок. Поэтому скобки принято опускать: + +...+ .

4. Для любого вектора

( )= .

5. Для любых векторов , уравнения x+ = и +x= имеют единственное решение x= +( ). Это решение  разность векторов и : x=  .

Правило построения разности векторов и вытекает из рис.2.1:

Для построения вектора  достаточно отложить векторы и из одной точки. Тогда вектор   вектор, начало которого совпадает с концом вектора , а конец  с концом вектора .

6. Для любых векторов , , ...,

( + +...+ )=  ... .

7. Для любого вектора имеет место равенство 0 = .

8. Для любого числа  имеет место равенство  = .

9. Если  = , то либо =0, либо = .

10. Для любого вектора и любого числа  имеет место равенство () = ( ), в частности, (1) =  .

11. Для любых чисел , ₁, ₂, …, _k и любых векторов , , , ..., имеют место равенства

(₁₂…_k) =₁ ₂ …_k

и

(  … )=  … .

Также, на множество векторов (как на плоскости, так и в пространстве) переносятся все понятия линейного пространства (например, линейная комбинация векторов, линейная зависимость (независимость) векторов и их свойства, базис и.т.д.).

2.1.2. Теорема. На плоскости максимальное число линейно независимых векторов равно 2, в пространстве  3. Любые k векторов, k>3 на плоскости и k>4 в пространстве, линейно независимы.

2.1.3. Теорема. На плоскости базис образует любая пара неколлинеарных векторов. В пространстве базис образует любая тройка некомпланарных векторов.

Таким образом, размерность линейного пространства геометрических векторов на плоскости равна 2, в пространстве  3. Это означает, что в любом базисе на плоскости вектор имеет две координаты: =(a_x, a_y). В пространстве в любом базисе вектор имеет 3 координаты: =(a_x, a_y, a_z). При этом, напоминаем:

2.1.4. Теорема. Если =(a_x, a_y), =(b_x, b_y),   произвольное число, то + =(a_x+b_x, a_y+b_y) и  =(a_x, a_y). В частности,  =(a_xb_x, a_yb_y)

Аналогичное свойство справедливо для векторов в пространстве.

Кроме того

2.1.5. Теорема. Два вектора и линейно зависимы тогда и только тогда, когда они коллинеарны, что равносильно пропорциональности их координат:

=  = (=)  на плоскости

=  = = (=)  в пространстве

Три вектора , и линейно зависимы тогда и только тогда, когда они компланарны, что равносильно

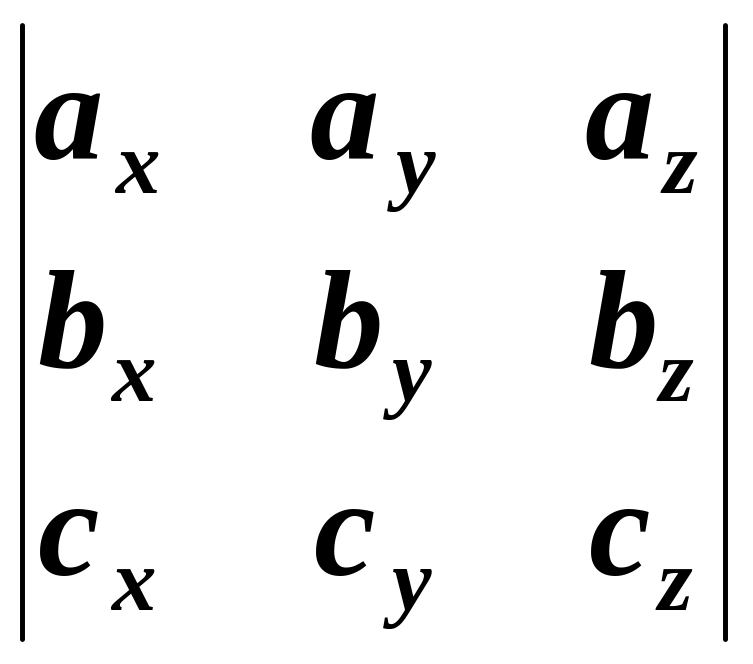=0.