Часть 1. Топографические съемки

1.1Обработка ведомости вычисления координат вершин точек теодолитного хода

Цель задания  освоить методику обработки теодолитных ходов.

Теодолитный ход представляет систему ломаных линий на мест­нос­ти, в которых углы измерены теодолитом, а стороны  20-метро­вой стальной линейкой.

Исходными данными для вычислений координат вершин теодо­литного хода являются горизонтальные углы в вершинах полигона и горизонтальные проложения длин сторон, дирекционный угол стороны ПП10-1 и координаты вершин ПП10 полигона (рис.). Координаты вершины и дирекционный угол задаются препо­давателем.

Исходный дирекционный угол линии 1-2

Исходный дирекционный угол линии ПП10-I (α _ПП10-I) известен и определяется в соответствии с вариантом, задаваемым препода­вателем, и фамилией студента: число целых градусов равно но­меру варианта студента, число минут равно 20,5' плюс столько целых минут, сколько букв в фамилии студента.

Например, Иванов - N_вap= 15 → α _ПП10-I =65°10‘ + 15°26,5‘=.80°36,5 Про­копьев – N_вap= 21 → α _ПП10-I =65°10‘ + 21°29,5‘=86°39,5‘ , α _ПП10-III = 179°29^/ +15°26,5^/ = 194°55,5^/ …

Исходные координаты точки 1

Исходные координаты точки ПП10 в системе плоских прямо­угольных координат известны. Они определяются в соответст­вии с номером варианта и номером группы студента: сотни мет­ров равны последней цифре номера группы, десятки и единицы метров, дробная часть равны номеру варианта.

Например, Иванов - N_гр = 21, N_ваp = 15 →X_пп10 = Yпп₁₀,= 115,15 м. Прокопьев – N_гp= 12, N_Bap= 23 → X_пп10 = Y_пп10 = 223,23 м.

Исходная отметка точки 1

Отметка точки 1 известна. Она определяется в соответствии с вариантом и номером группы студента: сотни метров рав­ны последней цифре номера группы, десятки и единицы метров равны номеру варианта, дробная часть повторяет целую.

Например, Иванов - N_гp =21, N_вap = 15 → Hпп₁₀ =115,115 м. Прокопьев - N_гp =12, N_вap=23→ Hпп₁₀ = 223,223 м.

Вычисления производятся в специальной ведомости (табл.) в следующем порядке.

1. В графу 1 ведомости последовательно вписывают наимено­вания точек хода.

2. Выписывают из журнала измерения углов в графу 2 ведомости средние значения горизонтальных углов.

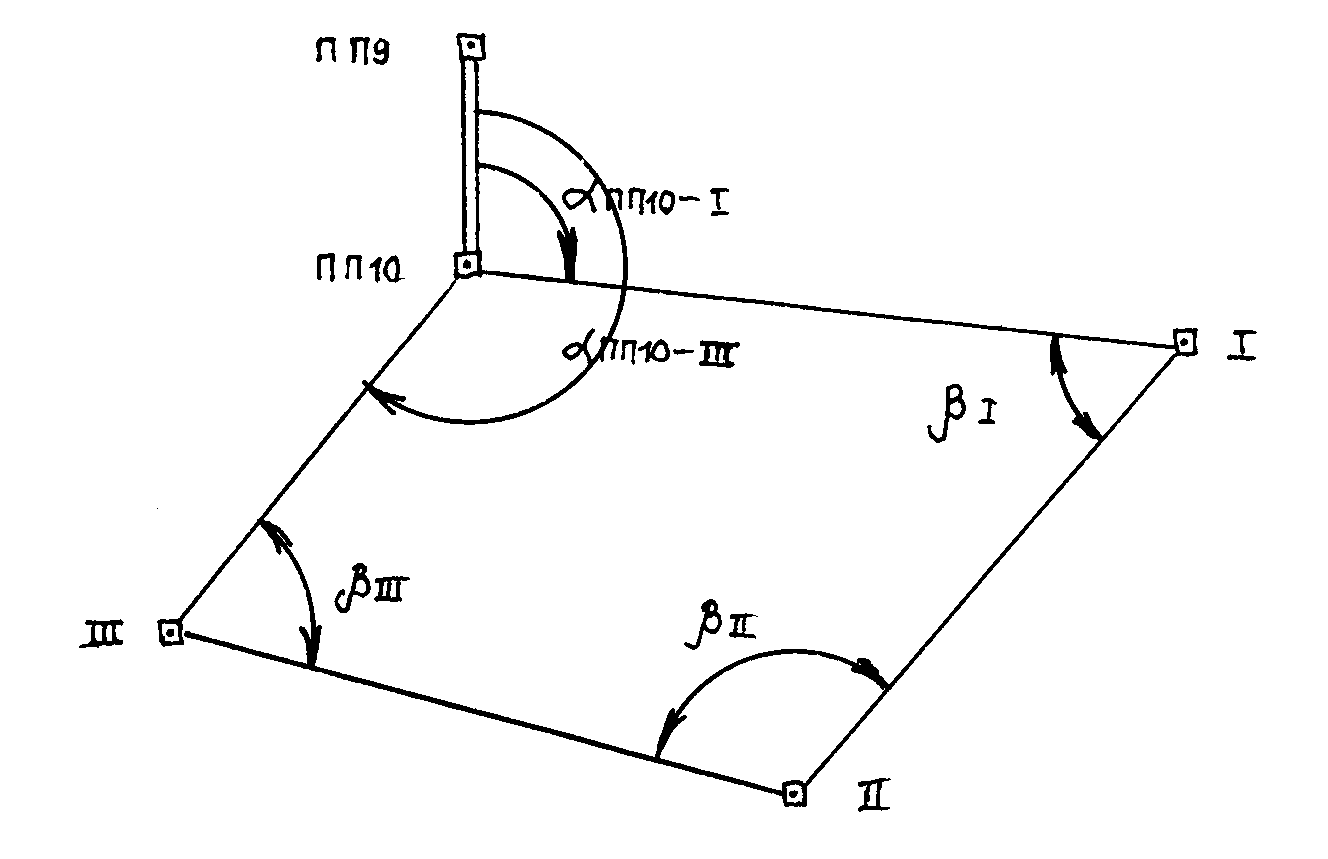
Рис. Схема теодолитного хода

3. Заносят в графу 5 ведомости значения дирекционного угла стороны ПП10-1 (задаются преподавателем), в графы 15 и 16-зна­чения координат x и y пункта ПП10 (задаются преподавателем).

4. В графу 8 ведомости выписывают горизонтальные проложе­ния сторон полигона (см.табл.16).

Результаты измерений углов и сторон

теодолитного хода

Углы		Стороны
номер вершин теодолитного хода	среднее значение горизонталь-ных углов и направлений	наименование сторон	горизонталь-ные проло-жения, м
I	7020,5	I-II	111,96
II	8059,5	II-III	93,49
III	9422,5	III-ПП10	66,39
ПП10	11419	ПП10-I	92,33
На ПП9	000
На т.I	6510
На т. III	17929
	(179296510=11419)

Значения горизонтальных проложений длин сторон располагают в строке, которая размещена с наименованием конечных точек стороны.

5. Выполняют оценку точности угловых измерений по замкну­то­му теодолитному ходу. Для этого:

 подсчитывают сумму измеренных углов по формуле

;

 вычисляют теоретическую сумму углов по формуле

,

где n  число углов в полигоне;

 находят практическую величину невязки f_ по формуле

;

 вычисляют допустимую угловую невязку f_доп

.

Результаты вычислений приведены под итоговой чертой граф 2-3 ведомости координат (см.табл.17).

Если , то ее распределяют поровну на все углы с обрат­ным знаком, то есть вводят поправку _i во все измеренные углы со знаком, обратным знаку невязки:

.

Поправки вводят с округлением до десятых долей минут. Для малых полигонов и коротких ходов с целью сокращения вычис­лений возможно введение поправок, чтобы округлить углы до целых минут.

Поправки записывают в графу 3 ведомости и вычисляют исправ­ленные углы по формуле

.

6. Контролируют правильность увязанных углов, для чего под­счи­тывают сумму и убеждаются в соблюдении условия

.

7. По исходному дирекционному углу и увязанным углам вычисляют дирекционные углы всех остальных сторон по формуле

,

где пос 	дирекционный угол последующей стороны;
пред 	дирекционный угол предыдущей стороны;
ур 	увязанный, вправо по ходу лежащий угол.

Вычисление дирекционных углов выполняют в рабочей тетради, располагая их столбиком. Если при вычислениях дирекционный угол какой-либо стороны окажется больше 360, то эту величину (период) следует отнять от полученного значения. Вычисления приведены применительно к графе 5 табл.17.

ПП10  I =	10451	rПП10  1 = ЮВ:7509
	+180
	28451
	 7020
I-II =	21431	rI-II = ЮЗ:3431
	+ 180
	39431
	 8059
II-III =	31332	rII-III = СЗ:4628
	+ 180
	49332
	 9422
	39910
	360
III-ПП10 =	3910	rIII-ПП10 = СВ:3910

Производят контроль вычислений, для чего получают дирек­ционный угол исходной стороны:

III  ПП10 =	3910
	+180
	21910
	11419
ПП10  I =	10451

Значения вычисленных румбов записаны в графы 6 и 7 табл.17, против соответствующих дирекционных углов.

Ведомость вычисления координат

Но-мер точек теодо-лит-	Изме-ренные углы и	По-прав-ки в углы 	Урав-нен-ные углы ур	Дирек-цион-ные углы i-k	Румбы ri-k			Гори-зон-таль-ное поло-жение
ного хода					наз-вание	вели-чина	линии di-к, м
1	2	3	4	5	6	7	8
ПП10	11419	0	11419
				10451	ЮВ	7509	92,33
I	7020,5	0,5	7020
				21431	ЮЗ	3431	111,96
II	8059,5	0,5	8059
				31332	СЗ	4628	93,49
III	9422	0,5	9422
				3910	СВ	3910	66,32
ПП10				10451

Р=364,10

Таблица

точек теодолитного хода

Вычисленные приращения координат		Поправки в приращения координат		Исправленные приращения координат		Координаты точек
XB, м	, м	x, м	y, м	Xур, м	, м	X, м	Y, м
9	10	11	12	13	14	15	16
						400,00	500,00
23,66	+89,25	+0,02	+0,02	23,64	+89,27
						376,36	589,27
92,25	63,44	+0,03	+0,02	92,22	63,42
						284,14	525,85
+64,39	67,78	+0,03	+0,02	+64,42	67,76
						348,56	458,09
+51,42	+41,89	+0,02	+0,02	+51,44	+41,91
						400,00	500,00

+151,81 +131,14 +115,86 +131,18

151,91 131,22 115,86 131,18

f_x= 0,10 f_y= 0,08

8. В ряде случаев полученные дирекционные углы целесо­образно перевести в румбы. Зависимость между дирекционными угла­ми и румбами приведена в табл.

Зависимость между дирекционными углами и румбами.

Знаки приращений координат

Пределы значений дирек-ционных углов	Чет-верть	Назва-ние румбов	Зависимость между рум-ба­ми и дирекцион-ными	Знаки приращений
			углами	X	Y
090	I	СВ	r = 	+	
90180	II	ЮВ	r =180		+
180270	III	ЮЗ	r = -180		+
270360	IV	СЗ	r = 360-	+	

9. В графе 8 ведомости подсчитывают длину хода

.

10. По горизонтальным проложениям d линий теодолитного хода и их дирекционным углам  или их румбам r вычисляют прира­щения координат X и Y по формулам:

(51)

Знаки приращения координат определяют в зависимости от знаков sin и cos или от названий румбов (см.табл.18).

Найденные значения приращений записывают в графы 9 и 10 ведомости.

11. Выполняют оценку точности линейных измерений.

Вычисляют практическую сумму приращений координат по осям и .

Вычисляют теоретическую сумму приращений координат и . В замкнутом теодолитном ходе = 0 и = 0.

Определяют невязки f_x и f_y в приращениях координат по формулам:

(52)

то есть практические суммы приращений координат являются невяз­ка­ми на соотвествующие оси.

По значениям f_x и f_y вычисляют абсолютное значение линейной невязки f_p в периметре хода:

(53)

Вычисляют относительную невязку в периметре теодолитного хода по формуле

(54)

Невязка считается допустимой, если она не превышает 1:2000 длины хода.

В предыдущем примере:

f_x = 0,10 м; f_y =  0,08 м;

f_p =

В этом случае относительная погрешность

= 0,14/364,10 = 1:2600, что меньше 1:2000.

12. Допустимую невязку в приращениях координат распре­де­ляют пропорционально длинам сторон d_i. Для этого определяют поправки по формулам:

(55)

Поправки _xi и _yi округляют с точностью до 0,01 м и запи­сы­вают их в графы 11 и 12 ведомости.

В нашем примере при распределении невязки f_x имеем:

_x1 =  (0,10/364,10) 9 2,33 = + 0,22;

_x2 =  (0,10/364,10) 111,96 = + 0,03;

_x3 =  (0,10/364,10) 93,49 = + 0,026 + 0,03;

_x4 =  (0,10/364,10) 66,32 = + 0,018 + 0,02.

Если сумма поправок с обратным знаком отличается от вели­чины невязки на 0,01 или 0,02 м, то некоторые поправки округляют в нужную сторону.

13. Определяют исправленные приращения координат по форму­лам:

(56)

и записывают их в графы 13 и 14 ведомости. Контролем вычис­ления служит равенство сумм вычислений исправленных прира­щений координат с их теоретическими значениями. В замкнутом теодолитном ходе эти суммы должны быть равны нулю.

14. По координатам начальной точки (ПП10) и исправленным приращениям вычисляют координаты остальных точек теодолитного хода по формулам:

. (57)

Полученные значения координат последовательно выписывают в гра­фы 15 и 16. Контролем правильного вычисления координат то­чек служит совпадение вычисленных координат точки ПП10 с их исходными значениями.

В нашем примере:

Х₁ = Х_ПП10 + X_1исп = 400,00  23,64 = 376,36 м;

Х₂ = 376,36  92,22 = 284,14 м;

Х₃ = 284,14 + 64,42 = 348,56 м;

Х_ПП10 = 348,56 + 51,44 = 400,00 м.