Содержание

1.Приведение параметров элементов механической части к одной расчетной скорости…………………………2

2. Баланс мощностей и энергетические характеристики электропривода……………………………….…………………4

3. Типовые статические нагрузки, активные и реактивные моменты (силы).......................………………………..5

4.Потерии КПД электроприводов в установившемся режиме………………………………………………..8

5. Уравнение движения двухмассовой электромеханической системы с упругими связями…………..…10

6. Потери и расход энергии в переходных процессах электроприводов с дпт с нв………………………...14

7.Уравнение движения абсолютно жесткой электромеханической системы……………………………….18

8.Способы снижения потерь и расхода энергии в п.п. эл.п дпт с нв…………………………………….…..29

9. Режимы преобразования энергии и ограничения, накладываемые на их протекание………………..….30

10. Система Г-Д, схема, режимы работы……………………………………………………………………....35

11. Жесткость механических характеристик. Устойчивость работы электропривода………………..……38

12. Система Г-Д, регулирование скорости…………………………………………………………………….40

13. Потери и расход энергии в переходных процессах асинхронного электропривода……………………42

1. Приведение параметров элементов механической части к одной расчетной скорости.

Д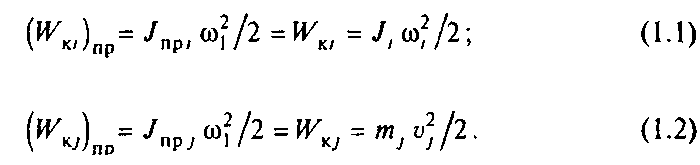 ля составления расчетных схем механической части электропривода необходимо приведение всех параметров элементов кинематической цепи к одной расчетной скорости. Обычно наибольшее удобство представляет приведение их к скорости двигателя, поэтому оно используется во всем последующем изложении. Однако следует иметь в виду возможность приведения к скорости любого элемента. В частности, при решении ряда задач оказывается полезным приведение к скорости механизма, особенно при поступательном движении его органа.

Условием соответствия приведенной расчетной схемы реальной механической системе является выполнение закона сохранения энергии. При приведении необходимо обеспечить сохранение запаса кинетической и потенциальной энергии системы, а также элементарной работы всех действующих в системе сил и моментов на возможных перемещениях. Соответственно при приведении момента инерции элемента системы, движущегося вращательно со скоростью _i или массы, поступательно движущейся со скоростью v к расчетной скорости _i должны выполняться условия

Откуда получаем формулы приведения

где i_1i=₁/_i - передаточное число от вала приведения до i-го вала; p_1j=v_i/₁ - радиус приведения к валу со скоростью ₁

При приведении вращательных _i и поступательных S_j перемещений необходимо учитывать, что передаточное число и радиус приведения определяются соотношением скоростей. Исходя из этого, в общем случае перемещения в системе связаны так:

При линейных кинематических связях i_1i=const и _1j=const. В этом случае формулы приведения перемещений имеют вид

При приведении жесткостей механических связей должно выполняться условие равенства запаса потенциальной энергии деформации упругих элементов. Соответственно

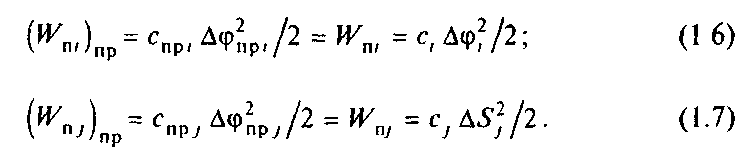
Откуда получим формулы приведения

Приведение моментов и сил нагрузки элементов кинематической цепи должно осуществляться на основании условия равенства элементарной работы на возможных перемещениях:

Следовательно,

При проектировании и исследовании электроприводов моменты инерции, массы, жесткости связей реальных элементов обычно бывают известны, а действующие в системе силы либо заданы, либо рассчитываются по исходным данным механизма и условиям его технологии. После приведения их значений к расчетной скорости представляется возможным, сопоставив приведенные значения моментов инерции и жесткостей, осуществить выбор главных масс и главных упругих связей и на этой основе составить приближенную расчетную схему механической части.

2. Баланс мощностей и энергетические характеристики электропривода

  Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками.

Баланс основан на законе сохранения и превращения энергии: сколько энергии выработали источники, столько же ее нагрузки должны потребить. Вместо энергии в балансе можно использовать мощность. Выработанная мощность всеми источниками должна быть равна суммарной мощности, расходуемой_в_нагрузках. Баланс мощностей можно сформулировать так: алгебраическая сумма мощностей источников, должна быть равна арифметической сумме мощностей нагрузок. Если направление ЭДС и направление тока ветви не совпадают, то составляющая мощности этого источника в балансе мощностей берется со знаком «минус».

Энергетические характеристики электропривода

К энергетическим характеристикам электропривода относятся рабочие характеристики, то есть зависимости тока, активной, реактивной и полной мощности, потребляемой от источника питания, от мощности на выходе электропривода (от мощности нагрузки): I₁, P₁, Q, S = f(P₂).

Эти характеристики определяют к.п.д. ( ) и коэффициент мощности ( ) электропривода. К энергетическим характеристикам также относятся зависимости средних, действующих и амплитудных токов через полупроводниковые элементы преобразователя от момента, скорости и мощности на выходе электропривода.

Наличие силового полупроводникового преобразователя, включенного между источником питания и двигателем, вносит определенную специфику, которую необходимо учитывать при анализе энергетических характеристик электропривода.

3. Типовые статические нагрузки, активные и реактивные моменты (силы), диссипативные моменты (силы). Кроме электромагнитного момента на механическую часть электропривода действуют статические нагрузки, которые делятся на силы и моменты механических потерь и силы и моменты полезных нагрузок исполнительных механизмов:       (2.9)

где первая составляющая суммы является суммарными потерями в двигателе и в исполнительном механизме, а вторая – суммарным приведённым моментом полезной нагрузки.

По характеру взаимодействия с электроприводом различаются активные и реактивные силы и моменты.

Активными силами и моментами называются силы и моменты, величина и направление которых не зависит от движения электропривода; например, силы и моменты, создаваемые перемещаемым по вертикали грузом. Механическая характеристика такого вида статической активной нагрузки изображена на рис. 2.5.

      

Рис. 2.5. Активные нагрузки электропривода неуравновешенного (а) и уравновешенного (б) подъемных механизмов

зависимости от соотношения масс   и   двигатель работает в тормозном (   ) или двигательном (   ) режимах.

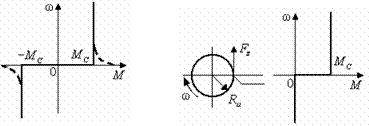
Силы и моменты, возникающие как реакции на движение электропривода, называются реактивными. Направление их всегда противоположно направлению движению электропривода. По характеру зависимости от скорости реактивных сил и моментов различают нагрузки типов сухого трения (рис. 2.6):

                  

a) б)

Рис. 2.6. Реактивные нагрузки: сухое трение (а) и момент резания (б).

В момент трогания силы сухого трения могут превышать свои значения при движении (рис. 2.6а).

Силы и моменты вязкого трения зависят от скорости линейно (рис. 2.7):

(2.10)

Рис. 2.7. Момент нагрузки типа вязкого трения.

 Момент внутреннего вязкого трения:       (2.11) где  и   – скорости на входе и выходе деформируемого элемента.

 По характеру влияния на механические колебания все силы и моменты делятся на консервативные и диссипативные.

  При действии консервативных сил и моментов не происходит поглощение колебаний. Например, сила тяжести является консервативной силой, т. к. работа, осуществляемая этой силой за период колебаний, всегда равна нулю.

  При действии диссипативных сил происходит поглощение энергии колебаний. Примером является вязкое трение, т.к. при изменении знака скорости изменяется и знак момента, а механическая мощность   сохраняет положительный знак, что соответствует поглощению колебаний.

  На практике распространённой является вентиляторная нагрузка (рис. 2.8):

Рис. 2.8. Зависимость момента от скорости при вентиляторной нагрузке

(2.12)

  Коэффициент полезного действия (КПД) механизма: η_мех=η₁η₂η₃ .., где η₁, η₂, η₃ – КПД элементов кинематической цепи.

 Если известен полезный момент нагрузки механизма M_мех, то для прямого направления энергии приведённый к валу двигателя момент статической нагрузки можно определить из равенства:

(   – момент механических потерь в двигателе.)  Следовательно,       (2.13)

где    - общее передаточное число от двигателя к рабочему органу механизма.

При обратном направлении потока энергии, когда нагрузка является активной и двигатель должен работать в тормозном режиме, уравнение баланса мощностей можно записать как:

  В этом случае       (2.14)

  Момент механических потерь в двигателе невелик, он составляет 1-5% номинального момента двигателя. Во многих практических случаях полагают   , т.к. точность определения момента M_мех невелика и он рассчитывается с некоторым запасом. При этом формулы приведения момента статической нагрузки к валу двигателя принимают вид:

  - для прямого направления передачи энергии (двигательный режим работы)       (2.15)

  - для обратного направления (тормозной режим работы)       (2.16)

  Если рабочий орган движется поступательно, то уравнение баланса мощностей имеет вид (ΔМ=0):

  Тогда       (2.17)

  Соответственно для обратного направления потока механической энергии       (2.18)

  Необходимо иметь в виду, что КПД передач зависит от нагрузки, а для червячного зацепления – и от направления передачи энергии, поэтому при расчётах следует использовать соответствующие зависимости η от полезной нагрузки передач.