7. Теоремы о четырёхугольниках

      Свойства параллелограмма.       У параллелограмма противолежащие стороны равны. У параллелограмма противолежащие углы равны.       Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам (рис. 96).

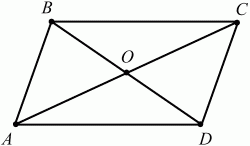
      Рис. 96.         АВ = CD, ВС = AD, ?BAD = ?BCD, ?АВС = ?ADC, AO = OC, BO = OD.         Признаки параллелограмма.       Если у четырёхугольника две стороны параллельны и равны, то он является параллелограммом (рис. 97).

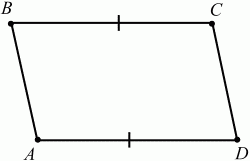
      Рис. 97.         ВС||AD, ВС = AD ? ABCD – параллелограмм.         Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм (рис. 98).

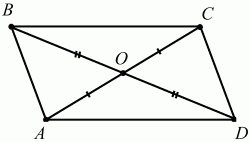
      Рис. 98.         АО = ОС, ВО = OD ? ABCD – параллелограмм.         Свойства прямоугольника.       Для прямоугольника характерны все свойства параллелограмма (у прямоугольника противолежащие стороны равны; у прямоугольника противолежащие углы равны (90°); диагонали прямоугольника пересекаются и точкой пересечения делятся пополам).       Диагонали прямоугольника равны (рис. 99):       АС = BD.

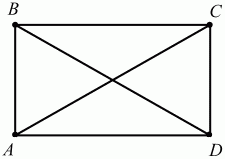
      Рис. 99.         Признак прямоугольника.       Если у параллелограмма все углы равны, то он является прямоугольником.         Свойства ромба.       Для ромба характерны все свойства параллелограмма (у ромба противолежащие стороны равны – вообще все стороны по определению равны; у ромба противолежащие углы равны; диагонали ромба пересекаются и точкой пересечения делятся пополам).       Диагонали ромба пересекаются под прямым углом.       Диагонали ромба являются биссектрисами его углов (рис. 100).

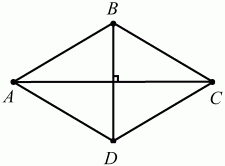
      Рис. 100.         AC ? BD, ?ABD = ?DВС = ?CDB = ?BDA, ?ВАС = ?CAD = ?ВСА = ?DCA.         Признак ромба.       Если у параллелограмма диагонали перпендикулярны, то он является ромбом.         Свойства квадрата.       Квадрат обладает свойствами прямоугольника и ромба.         Признак квадрата.       Если диагонали прямоугольника пересекаются под прямым углом, то он – квадрат.         Свойство средней линии трапеции.       Средняя линия трапеции параллельна основаниям и равна их полусумме (рис. 101).

      Рис. 101.

        Критерии вписанного и описанного четырехугольников.       Если около четырёхугольника можно описать окружность, то суммы его противоположных углов равны по 180° (рис. 102).       ?А + ?С = ?В + ?D = 180°.

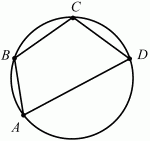
      Рис. 102.         Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны (рис. 103).       AB + CD = AD + BC.

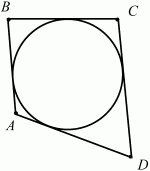
      Рис. 103.

8. Теоремы об окружностях

      Свойство хорд и секущих.       Если хорды АВ и CD окружности пересекаются в точке S, то AS ? BS = CS ? DS (рис. 104).

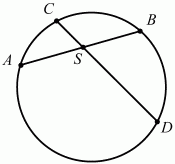
      Рис. 104.         Если из точки S к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AS ? BS = CS ? DS (рис. 105).

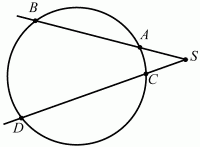
      Рис. 105.         Число ?.       Отношение длины окружности к её диаметру не зависит от радиуса окружности, то есть оно одно и то же для любых двух окружностей. Это число равно ? (рис. 106).

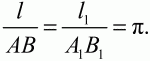
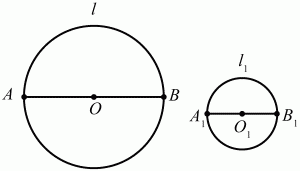
      Рис. 106.