2.3. Темы для сообщений и рефератов

      1. Замечательные точки в треугольнике. (1)       2. Вневписанные окружности. (1–2)       3. Радикальная ось и радикальный центр окружностей. Пучки окружностей. (3)       4. Полярное соответствие. Принцип двойственности в геометрии. (3)       5. Отображения и преобразования множеств. Композиция преобразований. Аффинные преобразования плоскости. (3)       6. Инверсия плоскости относительно окружности. (3)       7. Понятие длины. Расстояние между фигурами. (2)

§ 3. Важнейшие теоремы и формулы школьного курса планиметрии

3.1. Справочная информация

      Приведём без доказательства основные теоремы планиметрии.       Доказательства желательно изучать по вашему учебнику. Опасно изучать доказательство теорем по разным учебным пособиям – можно в погоне за простотой попасться на капкане «порочного круга». Приведём простой пример. Нужно доказать признаки параллельных прямых (если при пересечении двух прямых третьей сумма образовавшихся внутренних односторонних углов равна 180°, то прямые параллельны).       На рис. 56:m, n, a – прямые. Точка А – точка пересечения прямых m и а, В – точка пересечения прямых n и а.

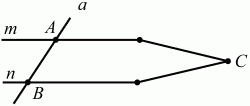
      Рис. 56.         Ученик привёл простое доказательство: если бы прямые m и n пересекались в некоторой точке С, то тогда из того, что сумма углов в треугольнике АСВ равна 180°, следует, что ?АСВ = 0°, что невозможно. Значит, прямые m и n параллельны.       Но тут же ученику предложили доказать, что сумма углов в треугольнике равна 180°. Учащийся сослался на свойства параллельных прямых. Но сами свойства параллельных прямых он стал доказывать на основе признаков параллельности прямых. Круг замкнулся. Поэтому в повторении теории будьте последовательны и внимательны. При чтении доказательства теоремы особое внимание обращайте на то, где в доказательстве использованы условия теоремы, какие ранее доказанные теоремы при этом использовались.       В настоящем параграфе формулировки теорем приведены по учебнику А. В. Погорелова «Геометрия. 7–9 классы».

Основные теоремы планиметрии и следствия из них

1. Теоремы о прямых (параллельность и перпендикулярность на плоскости)

      Свойства параллельных прямых.       Две прямые, параллельные третьей, параллельны (рис. 57).       (а||с, b||с) ? а||b.

      Рис. 57.         Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180° (рис. 58).       а||b ? ? = ?       ? + ? = 180°.

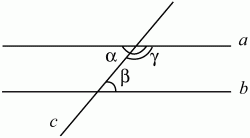
      Рис. 58.         Признаки параллельности прямых.       Если при пересечении двух прямых третьей образующиеся внутренние накрест лежащие углы равны, то прямые параллельны (рис. 59):       внутренние накрест лежащие углы равны ? а||b.

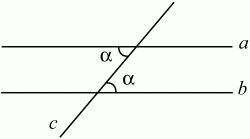
      Рис. 59.         Если при пересечении двух прямых третьей сумма образовавшихся внутренних односторонних углов равна 180°, то прямые параллельны (рис. 60):       а||b.

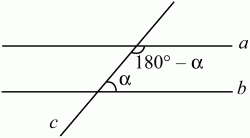
      Рис. 60.         Если при пересечении двух прямых третьей образующиеся соответственные углы равны, то прямые параллельны (рис. 61):       а||b.

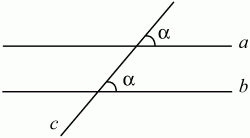
      Рис. 61.         Теоремы о существовании и единственности перпендикуляра к прямой. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну (рис. 62).

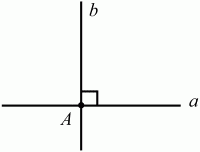
      Рис. 62.         Прямая b – единственная прямая, проходящая через точку А перпендикулярно а.       Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один (рис. 63).

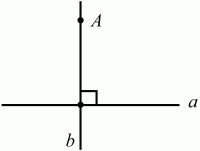
      Рис. 63.         Прямая b – единственная прямая, проходящая через точку А перпендикулярно а.         Связь между параллельностью и перпендикулярностью.       Две прямые, перпендикулярные третьей, параллельны (рис. 64).       (а ? с, b ? с) ? а||b.

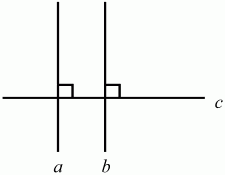
      Рис. 64.         Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой (рис. 65):       (а ? b, b||с) ? а ? с.

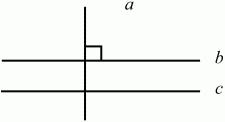
      Рис. 65.