Задачи для самостоятельного решения

      146. Доказать, что медиана треугольника меньше полусуммы заключающих ее сторон. (1)       147. Туристы находятся на острове «А». Им надо прибыть на остров «В», – при этом сначала побывав на обоих берегах реки. Каков будет их кратчайший маршрут (рис. 204)? (2)

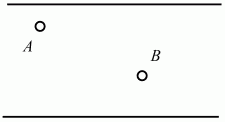
      Рис. 204.         148. Средняя линия трапеции равна 4; отрезок, соединяющий середины оснований, равен 1; углы при основании трапеции равны 40° и 50°. Найдите длины оснований трапеции. (3)

2.10. Задачи, решаемые координатным и векторным методами

      Вообще говоря, в данном случае речь идет не о частных идеях решения определенного класса задач, а об универсальных методах решения самых разнообразных геометрических проблем.       Суть метода состоит в том, что для решения задач вводится система координат (прямоугольная или аффинная), пишутся необходимые уравнения прямых, других фигур, по известным формулам находятся длины и углы.

Примеры решения задач

      149. Даны точки А(-2; 1); В(1; 5); С(3; -2); D(6; 2). Является ли четырёхугольник ABCD параллелограммом? Ответ: обоснуйте. (1)       Решение. АВ = (3; 4); CD = (3; 4). Противоположные стороны четырёхугольника, таким образом, равны и параллельны. Значит, ABCD – параллелограмм.       Ответ: ABCD – параллелограмм.         150. В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС (рис. 205). (2)

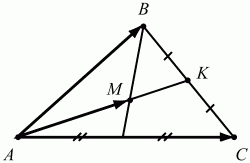
      Рис. 205.         Решение. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины, поэтому

      Задачу можно решить проще, если достроить треугольник ABC до параллелограмма ABDC, тогда AM = 2/3 АК, но АК = 1/2 AD = 1/2 (АВ + АС). Отсюда сразу получаем, что AM = 1/3(АВ + АС).       Ответ: 1/3(АВ + АС).         151. В прямоугольнике ABCD точки М и N – середины сторон АВ и ВС. Точка О – точка пересечения AN и DM. Найдите AO/ON (рис. 206). (2)

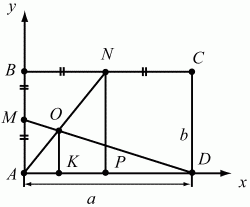
      Рис. 206.         Решение. Решим задачу аналитическим путём. Пусть А(0; 0); D (a; 0); B(0; b), тогда M(0; b/2); N(a/2; b). Напишем уравнения прямых AN и MD.

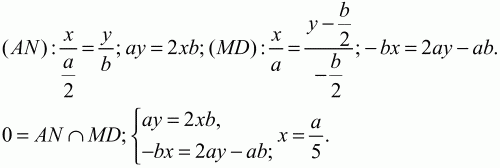
      Точка О будет иметь координаты:

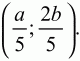
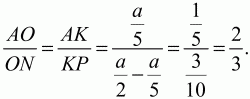
      Ответ: 2:3.         152. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC (рис. 207). (3)

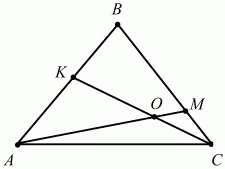
      Рис. 207.         Решение. См. задачу 105 (с. 88). Тогда мы решили её, применив теорему о пропорциональных отрезках. Здесь мы применим векторный подход и метод неопределенных коэффициентов.       Пусть ВА = а, ВС = b, АО = х ? AM, КО = у ? КС, тогда АО + ОК = АК, х ? АМ + (-у ? КС) = -1/2а.       Так как AM = AB + ВМ = – ВА + 3/4ВС = – а + 3/4b и КС = KB + ВС = -1/2ВА + ВС = -1/2а + b, то с учётом этого получаем уравнение: хAM + (-уКС) = -1/2а или х(-а + 3/4b) – у(-1/2а + b) = -1/2а. Приравнивая к нулю коэффициенты при векторах а и b, стоящих в левой и правой частях уравнения, получим систему:

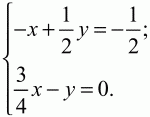
      х = 4/5, у = 3/5;       Итак,

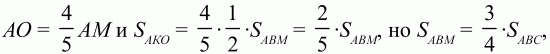
      значит,

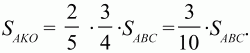
      Ответ: 3/10.         153. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3.       Найти косинус угла между векторами АВ и DC (рис. 208). (3)

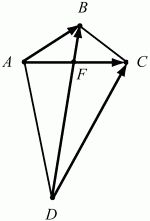
      Рис. 208.         Решение:       Пусть ? – искомый угол между векторами АВ и DC тогда

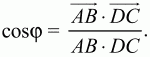
      Пользуясь свойствами скалярного произведения векторов и условиями задачи, вычислим АВ, DC и АВ ? DC. Так как

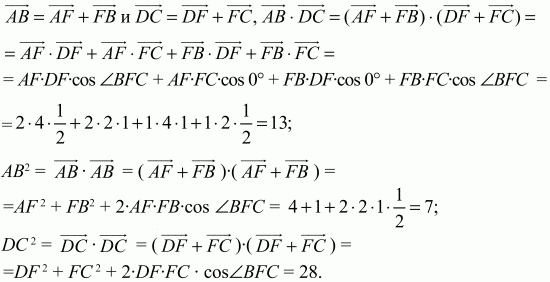
      Теперь получаем, что

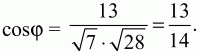
      Ответ: 13/14.