Задачи для самостоятельного решения
129. Четырёхугольник ABCD описан около окружности с центром О. Найдите сумму углов АОВ и COD. (1) 130. Определите площадь круга, вписанного в прямоугольную трапецию с основаниями а и b. (2) 131. Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно 5/11. Найдите длины оснований трапеции. (3)
2.7. Задачи на вписанные углы
Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.
Примеры решения задач
132. Найдите ?ТОК, если О – центр окружности и ?ТЕК = 120° (рис. 190).(1)
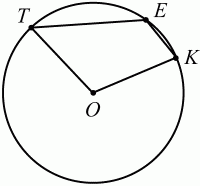
Рис. 190. Решение. Так как вписанный угол ТЕК равен половине центрального угла, опирающегося на ту же дугу, то
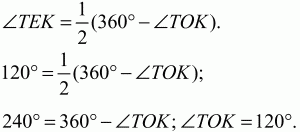
Ответ: 120° 133. Дан правильный 30-угольник А1А2 ... А30 с центром О. Найдите угол между прямыми ОА3 и А1А4 (рис. 191). (2)
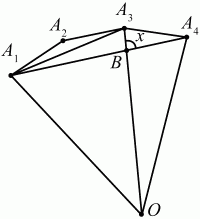
Рис. 191. Решение. Так как многоугольник А1А2 ... A30 – правильный, то ?А3ОА4 = 360°/30 = 12°. Далее, ?А3А1А4 = 1/2 ?А3ОА4 = 6° (вписанный угол, опирающийся на дугу А3А4). ?А1ОА3 = 2 ? 12° = 24°;
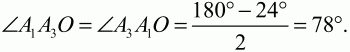
Требуемый нам угол х является внешним углом к треугольнику А3А1В. Так как внешний угол треугольника равен сумме внутренних углов, с ним не смежных, то х = 6° + 78° = 84°. Ответ: 84°. 134. В окружность вписан четырёхугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к АВ, пересекает сторону CD в точке М. Доказать, что ЕМ – медиана треугольника CED, и найти её длину, если AD = 8 см, АВ = 4 см и ?CDB = ? (рис. 192). (3)
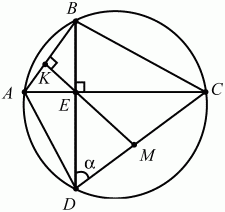
Рис. 192. Решение. Обозначим через К точку пересечения прямых АВ и ЕМ. Поскольку углы CDB и CAB опираются на одну и ту же дугу ВС, то ?CAB = ?CDB = ?. Из равенств ?DCE + CDB = ?/2, ?КЕА + ?САВ = ?/2, следует, что ?DCE = ?КЕА = ?СЕМ. Но это означает, что треугольник СЕМ равнобедренный, т. е. СМ = ЕМ. Далее, ?MED = ?/2 – ?СЕМ = ?/2 – (?/2 – ?) = ?CDB. Итак, треугольник EMD равнобедренный, или DM = ЕМ. Этим доказано, что СМ = DM или что ЕМ – медиана треугольника CED. Из прямоугольного треугольника ABE находим АЕ = АВ ? cos?ЕАВ = АВ ? cos?CAB = 4 ? cos ?. Далее, из прямоугольного треугольника AED по теореме Пифагора получаем
и, наконец,
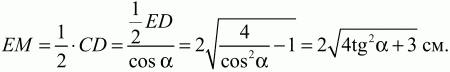
Ответ:
Задачи для самостоятельного решения
135. Окружности с центрами О и О1 касаются внутренним образом. Найдите угол В (рис. 193). (1)
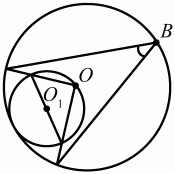
Рис. 193. 136. Точка находится внутри круга радиуса 6 и делит проходящую через неё хорду на отрезки длиной 5 и 4. Найдите расстояние от точки до окружности. (2) 137. а) Докажите, что
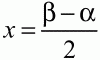
(рис. 194);
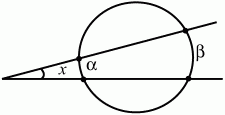
Рис. 194. б) докажите, что
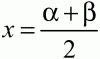
(рис. 195). (3)
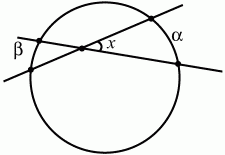
Рис. 195. 138. Диагональ BD четырёхугольника ABCD является диаметром окружности, описанной около этого четырёхугольника. Вычислить длину диагонали АС, если BD = 2, AB = 1, ?ABD:?DBC = 4:3. (3)