Примеры решения задач

      102. Докажите, что медианы в треугольнике делятся в отношении 2:1, считая от вершины (известная теорема школьного курса математики). (2)       Самый простой путь решения (рис. 173):

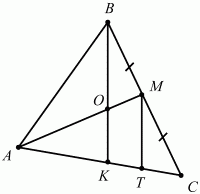
      Рис. 173.         Проведем медианы AM и ВК, а также отрезок МТ, параллельный ВК. Имеем: т. к. ВМ = МС, то КТ = ТС. Но тогда АК = КС = 2КТ и, значит, АО: ОМ = АК: КТ = 2, что и требовалось доказать.         103. В треугольнике ABC на стороне ВС взята точка М так, что MB = МС, а на стороне АС взята точка К так, что АК = 3 ? КС. Отрезки ВК и АМ пересекаются в точке О. Найдите AO/OM (рис. 174). (2)

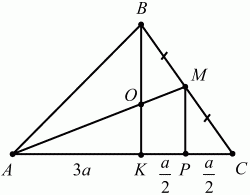
      Рис. 174.         Решение. Обозначим длину отрезка КС через а, тогда АК = За. Проведём MP||ВК По теореме Фалеса КР = РС = a/2. По теореме о пропорциональных отрезках имеем:

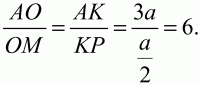
      Ответ: 6.         104. В треугольнике ABC на стороне АВ взята точка К так, что АК: ВК = 1:2, а на стороне ВС взята точка L так, что CL: BL = 2:1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника ABC, если дано, что площадь треугольника BQC равна 1 (рис. 175). (3)

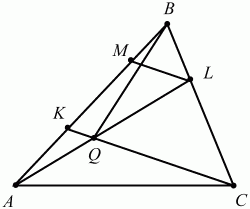
      Рис. 175.         Решение. Проведём через точку L прямую LM параллельно прямой СК. Из подобия треугольников MBL и КВС следует, что

      Из подобия треугольников AKQ и AML находим:

      Кроме того, имеем следующие равенства:

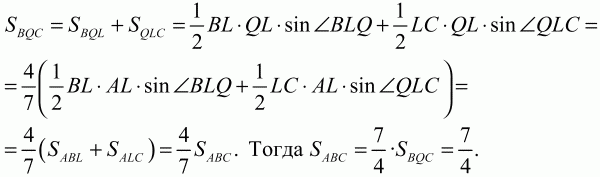
      Ответ: 7/4.

Задачи для самостоятельной работы

      105. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC(рис. 176). (2)

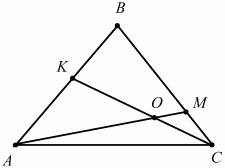
      Рис. 176.         106. На сторонах АВ и АС треугольника ABC взяты точки M и N, такие, что AM/MB = CN/NA = 1/2.       Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.(2)

2.4. Задачи на свойства биссектрисы треугольника

      Биссектриса треугольника обладает одним замечательным свойством: она делит противолежащую сторону на отрезки, пропорциональные соответствующим боковым сторонам (рис. 177).       с/а = d/b или c/d = a/b.

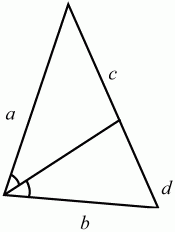
      Рис. 177.         Это свойство часто используется в задачах, в которых фигурирует биссектриса треугольника.

Примеры решения задач

      107. В треугольнике ABC проведена биссектриса AD. Найдите периметр треугольника ABC, если АС = 4; DC = 2; BD = 3 (рис. 178). (1)

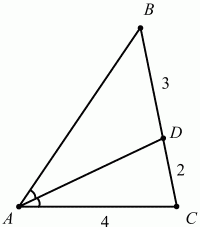
      Рис. 178.         Решение. По свойству биссектрисы BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.       Периметр треугольника РАВС = 6 + 5 + 4 = 15.       Ответ: 15.         108. Дан треугольник ABC, в котором ?В = 30°, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D. Определите площадь треугольника ABD (рис. 179). (2)

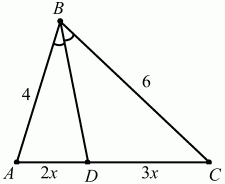
      Рис. 179.         Решение. По свойству биссектрисы AD/DC = AB/BC = 4/6 = 2/3.       Пусть AD = 2х; DC = Зх.

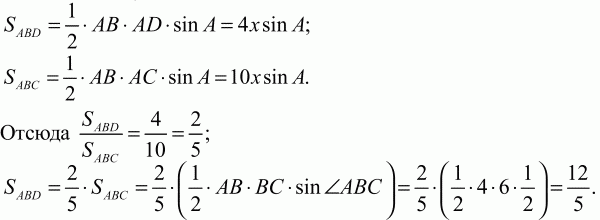
      Ответ: 12/5.

Задачи для самостоятельного решения

      109. В треугольнике ABC, где АВ = 6, АС = 4, биссектриса AL и медиана ВМ пересекаются в точке О. Найдите BO/OM (1).       110. Определите стороны треугольника, если медиана и высота, проведённые из вершины одного угла, делят этот угол на три равные части, а сама медиана равна 10 см. (2)