Задачи для самостоятельного решения

      64. Диагональ прямоугольника делит угол в отношении 2:1. Найдите отношение сторон прямоугольника. (1)       65. Площадь прямоугольника равна 9?3 см2, а величина одного из углов, образованного диагоналями, равна 120°. Найдите стороны прямоугольника. (2)       66. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка О так, что OB = OD = 13. Найти расстояние от точки О до наиболее удаленной от нее вершины прямоугольника. (3)

1.8. Задачи на квадрат

      Если а – сторона квадрата, d – его диагональ, то S = a2= d2/2.

Примеры решения задач

      67. Радиус окружности, в которую вписали квадрат, равен 6. Найдите площадь квадрата (рис. 159). (1)

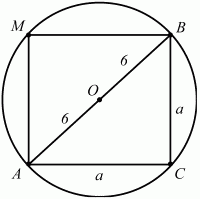
      Рис. 159.         Решение. Очевидно, что центр описанной около квадрата окружности есть точка пересечения его диагоналей. Это означает, что ОВ – радиус окружности и ОВ = 6. Тогда АВ = 12 и по теореме Пифагора AC2+ ВС2= AB2. Обозначив длину стороны квадрата через а, получим: а2+ а2= 122; 2 ? а2= 144; а2 = 72. Sквадрата = a2= 72.       Ответ: 72.         68. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого (2? – 4) см2. Найдите периметр квадрата (рис. 160). (2)

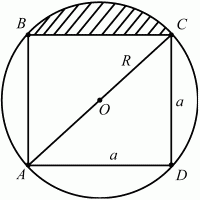
      Рис. 160.         Решение. Площадь заштрихованного сегмента, как видно из рисунка, можно вычислить по формуле:

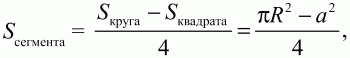
      где а – длина стороны квадрата, R – радиус описанной окружности. Выразим R через а.

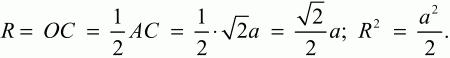
      Таким образом,

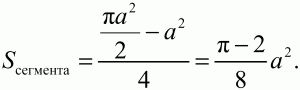
      С учётом условия получаем уравнение:

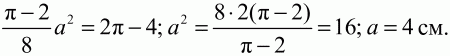
      Рквадрата = 4a = 4 ? 4 = 16 см.       Ответ: 16 см.         69. В плоскости дан квадрат с последовательно расположенными вершинами А, В, С, D и точка О. Известно, что OB = OD = 13, ОС = 5?2 и что площадь квадрата больше 225. Найти длину стороны квадрата и выяснить, где расположена точка О – вне или внутри квадрата (рис. 161). (3)

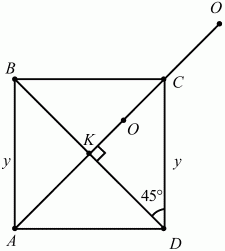
      Рис. 161.         Решение. Так как OB = OD, то точка О лежит на перпендикуляре к середине отрезка BD, т. е. на прямой АС. Обозначим через К точку пересечения диагоналей квадрата. Из условия следует, что ОВ > ОС; значит, точка О лежит по одну сторону с точкой С относительно перпендикуляра к середине отрезка ВС. Отсюда следует, что точка О лежит на луче КС.       Обозначим КО через х и АВ = CD через y. Так как

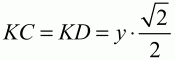
      и

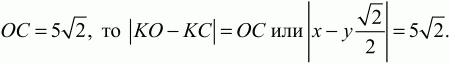
      Применяя к прямоугольному треугольнику KOD теорему Пифагора, получаем: OD2= КО2+ KD2или 169 = х2+ 1/2 у2.       Предположим, что КО ? КС или

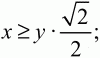
      тогда х2 ? 1/2 у2(заметим, что числа x и y неотрицательны) и

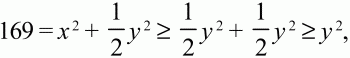
      т. е. площадь квадрата не превосходит 169, что противоречит условию. Следовательно,

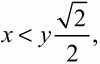
      т. е. КО < КС, и точка О лежит внутри квадрата. Теперь получаем

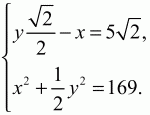
      Из первого уравнения

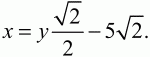
      Подставляя

      вместо х во второе уравнение, после арифметических преобразований получаем уравнение у2– 10у – 119 = 0. Это квадратное уравнение имеет корни у1 = -7 и у2 = 17. Так как у есть длина отрезка, то у > 0 и, значит, y = 17.       Ответ: длина стороны квадрата равна 17; точка О лежит внутри квадрата.