Задачи для самостоятельного решения

      43. Найдите площадь равнобокой трапеции, если ее основания равны 12 и 4 см, а боковая сторона образует с одним из оснований угол в 45°. (1)       44. Меньшее основание равнобедренной трапеции равно высоте и равно h. Острый угол трапеции равен 30°. Найдите периметр трапеции. (1)       45. Длины параллельных сторон трапеции равны 25 и 4, а длины боковых сторон равны 20 и 13. Найдите высоту трапеции. (2)       46. Основания трапеции равны а и b, боковые стороны равны с. Найдите длину диагонали трапеции. (2)       47. Определите длину высоты трапеции, если её основания равны 28 и 16 см, а боковые стороны равны 25 и 17 см. (2)       48. Найдите площадь равнобедренной трапеции, у которой высота равна 10, а диагонали взаимно перпендикулярны. (2)       49. В трапецию ABCD с основаниями AD и ВС и с боковыми сторонами АВ и CD вписана окружность с центром О. Найти площадь трапеции, если угол DAB прямой, ОС = 2 и OD = 4. (3)

1.5. Задачи на параллелограмм

      Площадь параллелограмма со сторонами а, b и углом ? между ними вычисляется по формуле S = absin ?. Можно также воспользоваться формулой S = 1/2 d1d2 sin? где d1, d2 – длины диагоналей, ? – угол между ними (или S = aha, где ha – высота). Если в параллелограмм можно вписать окружность, то это ромб. Если около параллелограмма можно описать окружность, то это прямоугольник.

Примеры решения задач

      50. В параллелограмме сумма двух противолежащих углов равна 132°. Найдите градусную меру каждого из углов параллелограмма (рис. 151). (1)

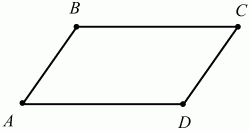
      Рис. 151.         Решение. По условию задачи ?А + ?С = 132°. Но, так как в параллелограмме противоположные углы равны, то ?А = ?С = 132°/2 = 66°. Учтём также, что ?А + ?В = ?С + ?D = 180°. Имеем:?В = ?D = 180° – 66° = 114°.       Ответ: 66°, 114°, 66°, 114°.         51. Одна из диагоналей параллелограмма разбивает его на два равносторонних треугольника со стороной а. Найдите длину другой диагонали (рис. 152). (1)

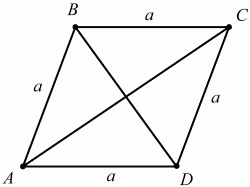
      Рис. 152.         Решение. Раз ?ABD и ?BCD – равносторонние, то углы ?BAD = ?BCD = 60°, тогда ?ABC = 120°.       По теореме косинусов из треугольника ABC получаем:

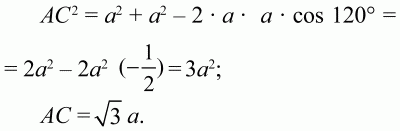
      Ответ:

        52. Найдите площадь параллелограмма, если его диагонали 3 и 5, а острый угол параллелограмма 60° (рис. 153). (2)

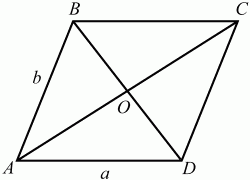
      Рис. 153.         Решение. Обозначим стороны параллелограмма: AD = а, АВ = b, ?BAD = 60°. BD = 3; АС = 5. Очевидно, что ?ABC = 120°. По теореме косинусов из треугольников ABD и АСВ имеем:

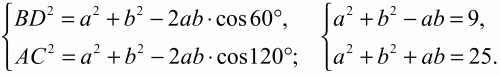
      Вычитая первое уравнение из второго, получим 2ab = 16. Тогда площадь будет равна:

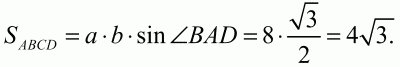
      Ответ:

Задачи для самостоятельного решения

      53. В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найдите длины сторон параллелограмма. (1)       54. В параллелограмме ABCD длина диагонали BD, перпендикулярной стороне АВ, равна 6. Длина диагонали АС равна 2?22. Найдите длину стороны AD. (1)       55. Параллелограмм ABCD, у которого АВ = 153, AD = 180, BE = 135 (BE – высота), разделен на три одинаковые по площади фигуры прямыми, перпендикулярными AD. На каком расстоянии от точки А находятся точки пересечения этих перпендикуляров с AD? (2)