Задачи для самостоятельного решения

      10. В треугольнике ABC высота AD на 4 см меньше стороны ВС. Сторона АС равна 5 см. Найдите периметр треугольника ABC, если его площадь равна 16 см2. (1)       11. Докажите, что для любого треугольника выполняется равенство:

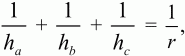
      где ha, hb и hc – высоты треугольника, а r – радиус вписанной окружности. (2)       12. Основание треугольника равно ?2. Найдите длину отрезка прямой, параллельной основанию и делящей площадь треугольника пополам.(2)       13. Найдите площадь треугольника по стороне а и прилежащим к ней углам ? и ?. (2)       14. В треугольнике ABC длина высоты BD равна 6 см, длина медианы СЕ равна 5 см, расстояние от точки пересечения отрезков BD и СЕ до стороны АС равно 1 см. Найти длину стороны АВ. (3)       15. В треугольнике ABC высота BD равна 11,2, а высота АЕ равна 12. Точка Е лежит на стороне ВС, и BE: ЕС = 5:9. Найти длину стороны АС. (3)       16. В треугольнике ABC длина стороны АС равна 3, ?ВАС = ?/6 и радиус описанной окружности равен 2. Доказать, что площадь треугольника ABC меньше 3. (3)       17. В треугольнике ABC медианы, проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ. (3)

1.2. Задачи на равнобедренный и равносторонний треугольники

      К задачам на равнобедренный треугольник применимы все формулы п. 1.1 этой главы, разве что во всех формулах b = с, ? = ?.       В случае равностороннего треугольника формулы значительно упрощаются, т. к. а = b = с, ? = ? = ? = 60°. Тогда

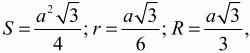
      длины всех медиан, высот и биссектрис равны

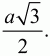
Примеры решения задач

      18. Один из углов равнобедренного треугольника равен 120°. Найдите отношение сторон треугольника (рис. 134). (1)

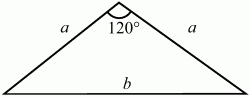
      Рис. 134.         Решение. Обозначим основание треугольника через b, боковые стороны через а (см. рис.). По теореме косинусов

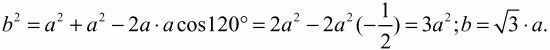
      Тогда отношения сторон треугольника а: а: в = 1:1:?3.       Ответ: 1:1:?3.         19. Найдите площадь круга, описанного вокруг равностороннего треугольника со стороной а (рис. 135). (1)

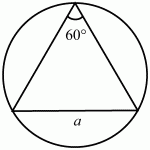
      Рис. 135.         Решение. Обозначим сторону треугольника через а. Тогда по теореме синусов имеем:

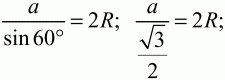
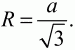
      Площадь круга:

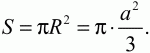
      Ответ:

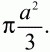
        20. Основание равнобедренного треугольника равно 4?2, медиана боковой стороны равна 5. Найдите длину боковой стороны (рис. 136). (2)

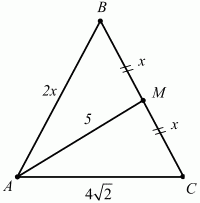
      Рис. 136.         Решение. Можно воспользоваться готовой формулой длины медианы:

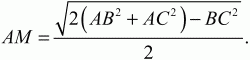
      Обозначим АВ через 2х, тотда ВМ = МС = х (см. рис.).       Имеем:

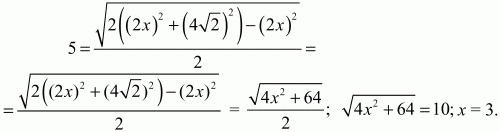
      АВ = ВС = 6.       Задачу можно решить по-другому. Из ?ABC по теореме косинусов:

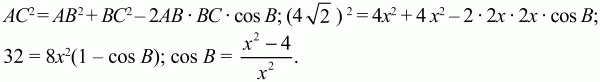
      Далее, по той же теореме косинусов из ?АМВ:

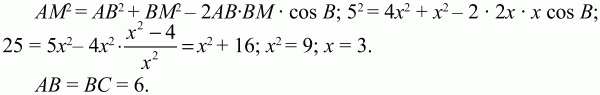
      Ответ: 6.         21. На основании равнобедренного треугольника, равном 8 см, как на хорде, построена окружность, касающаяся боковых сторон треугольника. Найдите радиус окружности, если длина высоты, опущенной на основание треугольника, равна 3 см (рис. 137). (2)

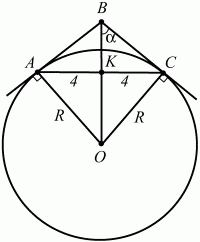
      Рис. 137.         Решение. Пусть данный треугольник ABC, где АВ = ВС; ВК = 3; АК = КС = 4 (см. рис.). Угол ОВС обозначим через ?. Из треугольника ВКС по теореме Пифагора находим:

      Из того же треугольника следует: tg ? = 4/3. Радиус окружности R = ОС найдём из треугольника ВСО:

      Ответ: 20/3 см.