3. Графический метод сложения взаимно-перпендикулярных колебаний

Наглядным является графический метод сложения взаим­но-перпендикулярных колебаний. Рассмотрим применение этого метода на примере сложения двух взаимно-перпендикулярных колебаний с равными частотами ( = l : l) и сдвинутых по фа­зе на величину = π/4. Разобьем эту процедуру на этапы.

Первый этап. Выберем начальную точку (точка 1) на вер­тикальной синусоиде, соответствующую времени t = 0 и началь­ной фазе = 0. На горизонтальной синусоиде точке с номером 1 будет соответствовать точка с начальной фазой = /4 колеба­ния (рис. 8.5).

Рис. 8.5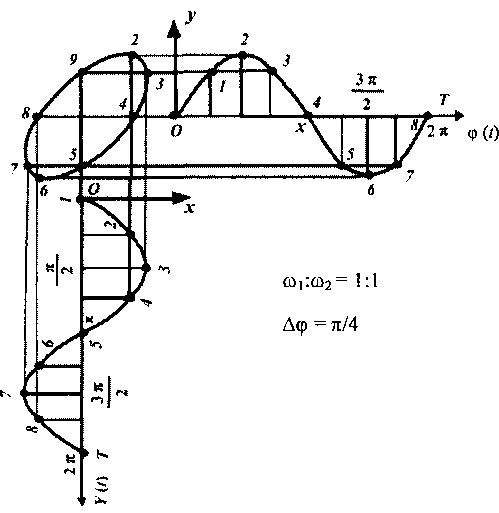

Второй этап. Из точки 1 на вертикальной синусоиде и точки 1 на горизонтальной синусоиде проведем прямые до их пересечения.

Третий этап. Пронумеруем точки,, соответствующие фа­зам π/4, 2π/4, Зπ/4, π и т. д., на вертикальной и горизонтальной синусоидах.

Четвертый этап. Из каждой пары точек синусоид прове­дем прямые линии до их взаимного пересечения в таком же по­рядке. Нумерацию точек пересечения проводим в таком же по­рядке, как и выбранные точки на синусоидах.

Пятый этап. Соединяем точки пересечения и получаем кривую, являющуюся результатом сложения взаимно- пепендикулярных колебаний, т. е. фигуру Лиссажу.

Подобным образом производят сложение колебаний, совер­шающихся с кратными периодами. Приведенный пример показы­вает, что графический метод сложения гармонических взаимно­перпендикулярных колебаний требует для построения достаточно много времени. Ниже, в ходе проведения лабораторной работы с использованием компьютерных технологий, продемонстрирова­но сложение гармонических взаимно-перпендикулярных колеба­ний, в результате которого получены соответствующие фигуры.

4. Фигуры Лиссажу

Во всех вышерассмотренных случаях частоты взаимно­перпендикулярных колебаний были одинаковы. Если это не так, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. Таким образом, фигуры Лиссажу воз­никают при сложении двух взаимно-перпендикулярных синусоидальных колебаний.

Н а рис. 8.6 показана одна из простейших траекторий, получающаяся при отношении частот = l : 2 и разности фаз π/2. В этом случае = 2 , а = . Уравнения колебания в этом случае имеют вид

.

Рис. 8.6

Когда частоты и , заметно отличаются одна от другой, картина получается очень сложной. Но она снова упрощается, если частота одного из колебаний в целое число раз больше частоты другого. При простых кратных соотношениях между частотами фигуры Лиссажу представляют собой замкнутые кривые, вписанные в прямоугольник со сторонами, равными удвоенным амплитудам происходящих колебаний. Можно оп­ределить по числу касаний траектории отношения между часто­тами колебаний. Если, например, фигура касается горизонталь­ной прямой один раз, а вертикальной - четыре (рис. 8.7, а), то это означает, что частота колебаний вдоль оси х в четыре раза больше, чем вдоль оси у (пока колебание, например, нач

Рис. 8.7. Фигуры Лиссажу для раз­личных соотношений частот , а —4:1; б-2:1; в — 2:3

авшись в точке М, в нее вер­нется, оно совершит четыре полных колебания по оси х).

Другой способ состоит в том, что определяют число пересечений между верти­кальной линией и фигурой Лиссажу и между горизон­тальной линией и фигурой Лиссажу (рис. 8.7, б, в). Число точек пересечения дает соот­ношение между частотами .Только вертикальная и горизонтальная линии не должны проходить точки пересечения на кривых фигур Лисса­жу. Например, нельзя проводить через точку L на рис. 8.7, в.

Следует отметить, что, чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. Если же соотношение между час­тотами иррационально, т. е. отношение нельзя предста­вить в виде отношения целых чисел, то это приведет к добавоч­ной разнице фаз. В результате картина колебания будет непре­рывно изменяться. Если частота одного из колебаний известна, то по виду фигур Лиссажу можно определить частоту другого.