3.6.Уравнение Клапейрона - Клаузиуса

Из молекулярно-кинетической теории известно, что атомы или молекулы в жидкостях и газах находятся в состоянии по­стоянного движения. Время от времени отдельные молекулы жидкости, движущиеся достаточно быстро, могут «срываться» с ее поверхности. Таким образом, над любой жидкостью какое- то количество молекул данного вещества будет находиться в виде пара. Давление этих молекул, если нет посторонних примесей, называется давлением пара этого вещества.

Ранее уже было отмечено, что для перевода вещества из жидкого состояния в газообразное нужно затратить некото­рую энергию (см. подразд. 2.2). Эта энергия называется тепло­той испарения или теплотой парообразования. Уравнение Клапейрона - Клаузиуса описывает отношение между теплотой испарения Н, давлением пара р и температурой вещества Т при равновесно протекающем процессе:

H = T (V₂ – V₁), (16.14)

где Т - температура перехода (процесс изотермический), К; dp/dT - производная давления по температуре на кривой фазо­вого равновесия; V₁ и V2 - удельные объемы вещества в исходной и конечной фазах соответственно.

Э

Рис. 16.7. Диаграмма цикла Карно для двухфазной системы в координатах Р - V.

ту зависимость в 1834 г. вывел инженер-конструктор па­ровых машин Бенуа Клапейрон. Он распространил метод, разра­ботанный Карно, для расчета коэффициента полезного дейст­вия (КПД) на процессы, проис­ходящие в области фазовых пе­реходов (рис. 16.7).

Напомним, что кoэффициент полезного действия (КПД) для тепловой машины

,

где Q - количество теплоты, сообщенное двигателю; А - работа, произведенная двигателем. Для нашего случая КПД цикла

= (V₂ -V₁) (16.15)

где - удельная теплота, сообщаемая единице массы системы при расширении; V₁ и V2 - удельные объемы фазы 1 и 2, т. е. объемы единицы массы, м³ /кг. С другой стороны, для цикла Карно КПД тепловой машины равен

(16.16)

где Т₁ - температура нагревателя; Т₂ - температура холодиль­ника. Поэтому в нашем случае (рис. 16.7) применение форму­лы (16.16) для расчета КПД даст выражение

= . (16.17)

В выражении (16.17) величиной dT в знаменателе, в силу ее малости, мы пренебрегаем. Из равенства правых частей уравнений (16.15) и (16.17) следует, что

= . (16.18)

Полагая, что Q₁₂ - удельная теплота, сообщаемая системе, равна удельной теплоте испарения Н, можно прийти к уравне­нию (16.14).

4. Порядок выполнения работы

В данной работе на экране компьютера имитируется сжа­тие различных веществ под поршнем в цилиндре. В результате сжатия происходит изменение агрегатного состояния вещества из газообразного в жидкое. В ходе опыта должны быть измере­ны объёмы вещества в жидком и газообразном состоянии, и давление насыщенного пара при каждой температуре. Для того чтобы выполнить задания виртуальной физической лабораторной работы, необходимо запустить программу, щелкнув левой клавишей мышки на экране (папка «Физ. лаб.»). После это­го на экране появится окно, в котором находится список лабора­торных работ. Установить курсор в разделе «Молекулярная физи­ка» на работе «Изучение фазового перехода испарение - конден­сация» и мышкой активизировать работу программы. В результате появляется окно, в котором присутствует таблица с командами:

• О работе

• Ход работы

• Эксперимент.

Последовательно вызывая пункты меню в таблице, необ­ходимо предварительно ознакомиться с лабораторной работой и порядком ее выполнения.

После обращения к команде Эксперимент появляется ок­но, где задаются начальные условия виртуального эксперимента (рис. 16.8).

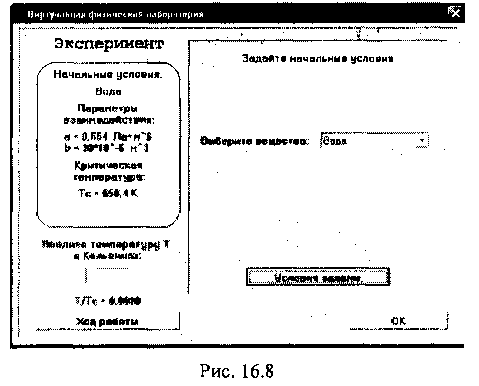
Для выполнения работы необходимо выполнить следую­щие действия:

1. Выбрать вещество. Для выбора вещества в соответст­вующем окне с его названием нужно нажать левую кнопку мы­ши. Появится список возможных вариантов. Из этого списка нужно выбрать необходимое для опыта вещество, при этом его параметры взаимодействия и критическая температура отобра­зятся в окне «Начальные условия». Выбрав рабочее вещество, нажать кнопку «Условия заданы». После нажатия кнопки «Ус­ловия заданы» появляется окно (рис. 16.8), на котором модели­руется процесс фазового перехода из одного агрегатного со­стояния в другое: газ-жидкость.

2. При температуре, равной 0,8 от критической (T/T_c измерить объёмы V₁ и V₂. Убедиться, что температура равна 0,8 от критической. Затем, меняя объём газа в цилиндре, отметить и записать значения объёмов V₁ и V₂, при которых появляется жидкость, занимая весь объем. Объём газа в цилиндре можно из­менить с помощью «ползунка», перемещая поршень вверх или вниз при нажатой левой кнопке мыши.

3. Измерить давление насыщенного пара при данной тем­пературе. Сначала, при уменьшении объёма газа, его давление рас­тет. Затем, как только в цилиндре появляется жидкость, давление газа некоторое время остается постоянным. При этом давлении (давлении насыщенного пара) жидкость и газ (пар) находятся в со­стоянии термодинамического равновесия (число молекул, выле­тающих из жидкости в пар, равно числу молекул, влетающих из пара в жидкость): они имеют одинаковые значения температуры и давления. Когда весь газ полностью перейдёт в жидкость, даль­нейшее уменьшение объёма вызывает резкий рост давления.

4.Опыт проделать при 6-8 различных значениях тем­пературы. Температуру можно задать путём введения соответ­ствующего числа в предназначенное для этого окно. Опыт следу­ет проделать для значений температуры в интервале от 0,80 до 0,99 от критической и при температуре, несколько выше крити­ческой. Температуру, давление насыщенного пара и оба значения объёмов записать в табл. 16.3.

5.Построить область двухфазного равновесия в пере­менных давление - объём. По оси ординат графика отложить приведенную температуру (Т/Т_с), а по оси абсцисс - значения объёмов V₁ и V2, соответствующие данной температуре.

6.Построить график зависимости давления насыщенно­го пара от температуры. По полученному графику оценить на­клон кривой при трёх значениях температуры. Для этого необхо­димо построить касательные к графику в соответствующих точках и определить тангенс угла наклона данной касательной.

Таблица 16.3

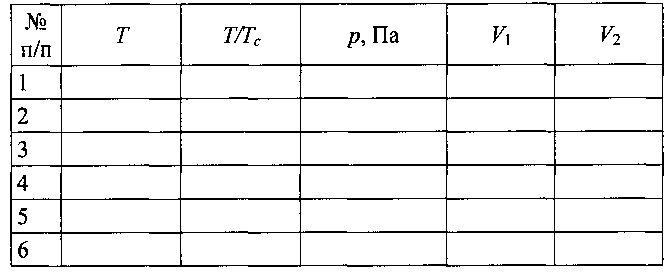
7.Оценить скрытую теплоту перехода с помощью уравнения Клапейрона-Клаузиуса по формуле (16.14). Оце­нить скрытую теплоту перехода при трёх выбранных ранее температурах, принимая, что производная dP/dT равна тангенсу угла наклона касательной. Сделать вывод на основании полу­ченных результатов.

Контрольные вопросы и задания

1. Сформулируйте цель работы.

2. Что такое агрегатное состояние вещества? Выделите главные отличительные признаки агрегатных состояний.

3. Дайте определение фазового перехода.

4. При какой температуре возможен переход вещества из газообразного состояния в жидкое? Какая температура назы­вается критической?

5. Что такое критическое состояние вещества?

6. Чем газовое состояние отличается от жидкого с позиций молекулярно-кинетической теории?

7. Какое состояние вещества называют паром?

8. Опишите последовательно процесс сжижения пара при его изотермическом сжатии.

9. Дайте определение конденсации.

10. Дайте определение испарения.

11. Дайте определение идеального газа.

12. Запишите уравнения, применяемые для описания со­стояния идеального и реального газов.

13. Какой пар называется насыщенным? Почему при сжа­тии насыщенного пара его давление остается постоянным?

14. В чем заключается сущность метода определения кри­тической температуры Каньяра де ля Тура?

15. Почему при сжатии жидкости давление резко возрастает?

16. Запишите формулу для расчета КПД цикла Карно.

17. Запишите уравнения Клапейрона-Клаузиуса.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература

1. Трофимова, Т.И. Курс физики (учебное пособие для технических специальностей ВУЗов) / Т.И. Трофимова. - М.: Издательский центр «Академия», 2007, 2008. - 560 с.

Дополнительная литература

2. Сивухин, Я.В. Общий курс физики. Т.1 / Я.В. Сивухин. - М.: Наука, главная редакция физико-математической литературы, 1979. - 519 с.