2. Описание экспериментальной установки

Схема экспериментальной установки для проверки теоре­мы Гюйгенса - Штейнера и определения момента инерции твердого тела изображена на рис. 6.8. Тело 1, момент инерции которого J_X необходимо определить, имеет форму шара с коль­цом и двумя симметрично расположенными стержнями. При этом дополнительные грузы 2 - малые шары - надеваются на стержни и могут быть установлены на различных расстояниях d от оси симметрии OO' установки. Стержень из металлического материала прикреплен к телу 1 с двух сторон и закреплен в кронштейнах 3 (на схеме рис. 6.8 изображен в виде оси ОО').

Для приведения системы в колебательно-вращательное движе­ние необходимо приложить момент силы - повернуть двумя ру­ками стержни на угол 8-10° (при малых углах период колеба­ний не зависит от амплитуды колебаний).

Рис. 6.8

5.3. Экспериментальная часть

Задание. 1. Определение момента инерции J_X крутиль­ного маятника.

1. Проведите измерения периода колебаний То крутильно­го маятника без дополнительных грузов не менее трех раз. Для более точного измерения периода необходимо измерить время t не менее как десяти полных колебаний, а затем опреде­лить период как Т = Здесь п - число полных колебаний.

Определите среднеарифметическое значение периода кру­тильных колебаний. При этом угол отклонения маятника из по­ложения равновесия не должен превышать 5 8°.

2. Установите дополнительные грузы на концах стержней так, чтобы их край совпадал с краем стержня. В таком положе­нии центры масс шаров будут находиться на расстоянии 0,2 м от оси вращения ОО'. Измерьте период Т₁ (см. п. 1).

3. Измерьте периоды Т₂, Т₃...,Т₆, последовательно пере­двигая шары на 2 см к центру (см. п. 1).

Заполните табл. 6.2.

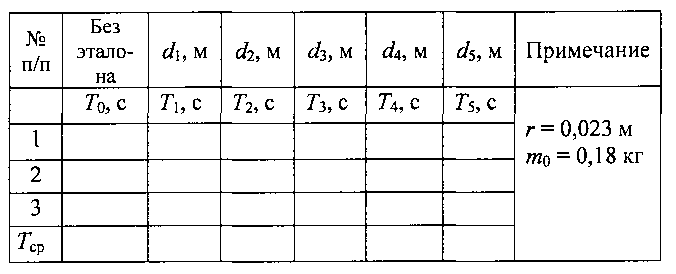
4. Измерьте диаметр шаров-грузов, найдите величину их радиуса. Определите общую массу двух шаров.

5. Для того, чтобы убедиться в правильности теоремы Гюйгенса - Штейнера, постройте график зависимости T² как функцию от d²(T² = f(d²)). В случае если получите линейную зависимость Т² от d² в виде T² = ad² + c, то это и будет под­тверждением справедливости теоремы Гюйгенса - Штейнера.

6. По тангенсу угла наклона, равному 2т₀, определите коэффициент угловой жесткости материала

7. Численное значение квадрата периода колебаний

в точке А (рис. 6.9) равно ).

Из равенства = ) выразите аналитически J_X. Подставив

численные значения , , т₀ и r², определите J_X, используя выражение

J_{X =} .

Рис. 6.9

По предложению преподавателя выполните дополнитель­ное задание.

Задание. 2. Определение момента инерции J_X крутиль­ного маятника.

1. Вычислите момент инерции J_X по формуле (6.23).

2. Сравните вычисленное значение J_X и полученное на ос­новании эксперимента значение J_X (см. п. 7 задания 1).

3. Сделайте вывод о справедливости теоремы Гюйгенса- Штейнера и о совпадении момента инерции J_X, рассчитанного по формуле и определенного из графика.

Контрольные вопросы и задания

1. Сформулируйте цель работы.

2. Какая физическая величина называется моментом инер­ции материальной точки, твердого тела?

3. Каков физический смысл понятия момента инерции?

4. Сформулируете теорему Гюйгенса - Штейнера.

5. В каких случаях затруднителен аналитический расчет момента инерции тела? Как поступают в этом случае?

6. Каков физический смысл коэффициента угловой жест­кости или модуля кручения подвеса?

7. Какие колебания называются крутильными?

8. В чем состоит метод проверки справедливости теоремы Гюйгенса-Штейнера, используемый в данной работе?

9. Какова зависимость от в предлагаемой работе? Ка­ковы цели, построения этого графика.

10. Объясните метод определения модуля кручения подве­са, используемый в данной работе.

11. Какие физические величины влияют на период коле­баний маятника, используемого в данной работе?

Вариант 3

6. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ

ОДНОРОДНОГО ДИСКА МЕТОДОМ КОЛЕБАНИЙ

1. Описание метода измерения

Как и в предыдущих вариантах определения моментов инерции твердых тел, в настоящем случае используется метод колебаний. Однако, если варианты 1 и 2 рассматривают колеба­ния относительно вертикальной оси, то в данном случае ось вращения твердого тела горизонтальна и не проходит через центр масс (тяжести) тела.

Такое тело, будучи выведено из состояния устойчивого равновесия, начнет совершать под действием силы тяжести колебания относительно этой оси. То есть мы будем иметь дело с физиче­ским маятником. Физическим ма­ятником называется абсолютно твердое тело, способное совершать колебания под действием силы тяже­сти вокруг неподвижной точки О, не совпадающей с центром масс С.

Найдем выражение для периода ко­лебаний физического маятника. Для этого рассмотрим колебания некото­рого тела, обладающего массой т, ось вращения которого O₁O₂ горизонтальна и проходит через точку О, находящуюся на рас­стоянии от центра тяжести тела С (рис. 6.10).

Рис. 6.10

Момент силы тяжести, действующей на тело относительно оси O₁O₂ имеет величину М = mg sin , и уравнение динамики вращательного движения тела примет в данном случае вид:

J

где -величина углового ускорения. Знак минус в равенстве (6.24) обусловлен тем, что вектор момента сил тяжести и вектор угла поворота направлены по оси вращения, но в противопо­ложные стороны

(рис. 6.11).

Если углы поворота тела относительно положения равно­весия малы, то можно считать, что sin и уравнение (6.24) имеет вид:

+ = 0. (6.25)

Уравнение (6.25) описывает колебательное движение тела относительно оси O₁O₂ и представляет собой дифференциаль­ное уравнение. Решение уравнения имеет вид:

= sin ( t + ), (6.26)

где - максимальный угол отклонения от положения равнове­сия, который является амплитудой в уравнении; ( t + ) - фаза колебания; - начальная фаза колебания; - циклическая час­тота колебаний, которая связана с период колебаний физического маятника Т следующим соотношением = . В нашем

случае Тогда период колебаний физическо­го маятника равен

Т = 2 . (6.27)

Таким образом, по формуле (6.27) можно найти период колебаний для любого физического маятника, при условии малых углов поворота маятника относительно положения равновесия.

К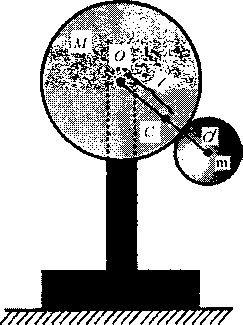 олебания, которые совершает физический маятник, от­носятся к простейшим типам колебаний, гармоническим коле­баниям, при которых движение те­ла в зависимости от времени описы­вается по синусоидальному (или косинусоидальному) закону.

Рассмотрим физический ма­ятник, состоящий из однородного диска, горизонтальная ось враще­ния которого проходит через центр тяжести и к ободу которого при­креплен шарик.

Если масса диска М, масса шарика т, момент инерции диска относительно данной оси J_Д, а момент инерции диска относительно этой же оси J_Ш, то для перио­да колебаний этого маятника на основании (6.27) имеем:

Рис. 6.11

Т = 2 . (6.28)

где = момент инерции данного физического маятника.

Поскольку проводить измерения расстояния от оси вра­щения маятника до центра тяжести (С) затруднительно, исклю­чим величину из формулы (6.28). Для этого воспользуемся ус­ловием равновесия тела относительно оси, проходящей через центр масс тела (рис. 6.12) (правило моментов).

У

словие равновесия нашей системы относительно оси, проходящей через центр тяжести системы (С), имеет вид:

Mg = (х + r)mg,

где отрезок х = R- и R- радиус диска (рис. 6.12); r - радиус

маленького шарика; - расстояние от цен­тра диска до центра тяжести диска с шари­ком; m - масса шари­ка; М- масса диска. Подставляя в условие равновесия значения x , получим:

М =(R- ) m.

Решим это уравнение относительно и по­лучим выражение

= .

Рис. 6.12

Подставим это значение в (6.27) и запишем период колебаний физического маятника в виде

T = 2 (6.29)

Теперь возведем обе части уравнения (6.29) в квадрат и выра­зим момент инерции диска :

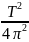= (R+r)mg - . (6.30)

Для вычисления момента инерции шарика применим тео­рему Штейнера: момент инерции J относительно произвольной оси равен моменту инерции J₀ относительно оси, параллельной данной и проходящей через центр масс тела, сложенной с произ­ведением массы тела т на квадрат расстояния а между осями:

J= Jo + т а².

Т

Рис. 6.13

огда, согласно теореме Штейнера, для нашего случая момент инерции шарика J_Ш от­носительно оси вращения диска O1O2 запишем в виде (рис. 6.13)

J_Ш ⁼ Jo + m(R+r)², (6.31)

где Jo - момент инерции шара относительно оси, проходящей через тяжести шара,

Jo = 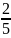m ,

получим из выражения для момента инерции диска в виде

= (R+r)mg - m . (6.32)