Л

Рис. 6.2

абораторная работа № 6

ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ

1. ЦЕЛЬ РАБОТЫ

Определение моментов инерции набора тел. Проверка теоремы Гюйгенса - Штейнера.

2. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

Трифилярный подвес, крутильный (торсионный) маятник, грузы, секундомер, штангенциркуль, весы.

3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Как известно из динамики, момент инерции - это физиче­ская величина, характеризующая распределение масс в теле от­носительно оси вращения и являющаяся мерой инертности тела при вращательном движении.

М

Рис. 6.1

оментом инерции материальной точки J, относительно какой-либо неподвижной оси называется произведение ее мас­сы на квадрат расстояния , до этой оси:

= Δ (6.1)

Поскольку масса реального тела представляет сумму со­ставляющих его масс материальных точек, то момент инерции тела J есть совокупность моментов инерции материаль­ных точек:

(6.2)

Момент инерции твердого тела относительно некото­рой оси OO´ проходящей через его центр масс, равен сумме моментов инерции всех точек тела от­носительно этой оси (рис. 6.1). Единица измерения момента инерции в СИ - кг м².

При непрерывном распределении масс сумма (6.2) сводится к интегралу

J = dm, (6.3)

где интегрирование проводится по все­му объему тела. Поскольку dm = ρdV, то момент инерции тела, имеющего плотность ρ, вычисляется по формуле

J= dV, (6.4)

где dV- элемент объема. Как видно из формул (6.1) - (6.4), мо­мент инерции относительно данной оси, как и масса, тела не зависит от характера движения. Он определяется размерами, формой и плотностью тела.

Для тел правильной геометрической формы интегрирова­ние дает следующие результаты для моментов инерции, вычис­ленных относительно оси, проходящей через центр симметрии этих тел (рис. 6.2). Здесь r - радиус соответствующих тел; т - их масса.

Если необходимо рассчитать момент инерции тела отно­сительно оси АA', проходящей не через центр симметрии, а параллельно ей (рис. 6.3), то используют теорему Гюйгенса- Штейнера:

J=J₀ + md², (6.5)

где т - масса тела; d- расстояние между осями.

Если момент инерции относительно оси, проходящей через центр масс равен Jo, то момент инерция тела относительно любой другой оси, параллельной первой, ра­вен моменту инерции Jo этого тела относительно оси ОО', сложенному с величиной md².

Основной закон дина­мики вращательного дви­жения имеет вид:

= (6.6)

где - величина суммар­ного момента внешних сил, действующих на тело; - угловая скорость тела. Если = 0, то J = const. Вели­чина = J называется моментом импульса твердого тела. Таким образом, если мо­мент сил, действующих на тело, равен нулю, т. е. система замк­нута, и тело будет покоиться или вращаться бесконечно дол­го, сохраняя постоянный мо­мент импульса. Это утвержде­ние, в сущности, является од­ной из формулировок закона сохранения момента импульса:

= const при = =0. (6.7)

В случае вращательного движения момент инерции J иг­рает ту же роль, что и масса т при поступательном движении, а угловая скорость - роль линейной скорости .

В табл. 6.1 сопоставлены величины и соотношения, яв­ляющиеся эквивалентными при поступательном и вращатель­ном движении тела. Видно, что момент инерции J является важной характеристикой вращательного движения, количест­венная информация о которой необходима при решении раз­личных задач.

Таблица 6.1

Момент инерции тел правильной геометрической формы может быть вычислен теоретически по формулам (6.2), (6.4) и (6.5). В случаях, когда аналитическое определение момента инерции затруднено сложностью формы тела или неоднородно­стью распределения массы (маховое колесо, коленчатый вал, винт и др.), его определяют опытным путем, что является одной из целей настоящей работы.

Имеются разные способы определения этой величины. В данной работе рассматриваются методы определения мо­ментов инерции твердых тел с помощью трифилярного под­веса и крутильного (торсионного) маятника, а также ком­пьютерный вариант определения момента инерции одно­родного диска.

Вариант 1

4. Определение моментов инерции твердых тел и проверка теоремы гюйгенса - штейнера с помощью трифилярного подвеса

   1. Описание рабочей установки и метода измерения

Одним из методов экспериментального определения мо­мента инерции является метод крутильных колебаний трифилярно подвешенного диска (трифилярного подвеса).

Трифилярный подвес состоит из большого диска Р, мас­сой т, радиусом R (рис. 6.4), подвешенного на трех симметрич­но расположенных капроновых нитях, и малого неподвижного диска Р' радиусом r, укрепленного на кронштейне. При поворо­те нижнего диска Р вокруг вертикальной оси OO' на некоторый угол а возникает момент сил, стремящийся вернуть диск в по­ложение равновесия. Диск Р начнет совершать крутильные ко­лебания относительно оси OO'. Если угол α мал (α =1-5°), в этом случае можно считать, что диск совершает гармониче­ские колебания.

Рис. 6.4

Гармоническим крутильным колебанием тела называется периодическое движение относительно вертикальной оси, про­ходящей через центр тяжести этого тела, когда угол отклонения от положения равновесия изменяется по закону синуса или ко­синуса. Например:

α = α₀sin( t+ ₀). (6.8)

Очевидно, что период колебаний подвеса будет зависеть от момента инерции системы (нижний диск и какое-либо тело на нем), а также от различных постоянных для данного трифилярного подвеса величин (длины нитей , радиусов верхнего и нижнего дисков r и R).

Воспользуемся законом сохранения энергии для того, чтобы найти связь периода колебаний трифилярного подвеса с его моментом инерц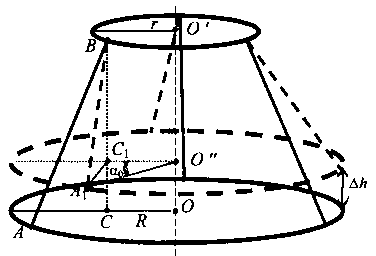 ии. При повороте нижнего диска Р на некоторый угол α_о относительно по­ложения равнове­сия он поднимает­ся на высоту Δh = h₁ - h2 (рис. 6.5), при этом прираще­ние потенциальной энергии равно:

ΔE_пот = mgΔh. (6.9)

При вращении диска в другую сторону потенциальная энергия переходит в кинетическую энергию вращательного движения.

Е_кин = J (6.10)

где J - момент инерции платформы; ω - угловая скорость плат­формы.

В момент прохождения положения равновесия кинетиче­ская энергия принимает максимальное значение. Тогда, пренеб­регая работой сил трения, на основании закона сохранения ме­ханической энергии имеем:

mgΔh = J _max, (6.11)

где - угловая скорость платформы в момент достижения положения равновесия.

Считая, что платформа совершает гармонические колеба­ния согласно (6.8), можно найти угловую скорость, взяв произ­водную от α

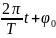ω = = cos( ) (6.12)

В нашем случае = , так как при t = 0 α = α₀.

В момент прохождения через положения равновесия

(t = T, Т , Т , Т и т.д.) абсолютное значение этой величины будет

= . (6.13)

На основании выражений (6.9), (6.10) и (6.11), (6.13)

mg Δh = J ( ) ² (6.14)

Из рис. 6.5 видно, что Δh можно выразить через парамет­ры трифилярного подвеса:

R - радиус диска платформы;

- длина нитей подвеса; r - радиус верхнего диска.

Δh = = = .

но (ВС)² = (АВ)² – (AC) ²= ²-(r- R)²,

(ВС₁)² = (А₁В)² - (A₁C₁)² = ²-(R² + r² - 2R r cos α₀),

следовательно,

Δh = = .

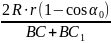При малых углах отклонения sin можно заменить углом α, а ВС + ВС₁= 2 и получим:

Δh = . (6.15)

Подставляя (6.15) в (6.14), можно записать:

mg = J .

Откуда J = . (6.16)

Учитывая, что параметры (R, r, ) во время опыта не изме­няются, формулу (6.16) удобно записать в виде

J = k т Т², (6.17)

где k = .

Формула позволяет вычислить момент инерции платформы с телом и без по измеренной величине периода Т.