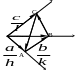
1 .4. Кристаллографические символы.

Символы узла. Положение любого узла в пространственной решетке определяется вектором

, m,n,p – однозначно определяют положение узловой точки. Обозначают [[mnp]] - символ узла. Знак минус пишется над цифрой.

Пример:

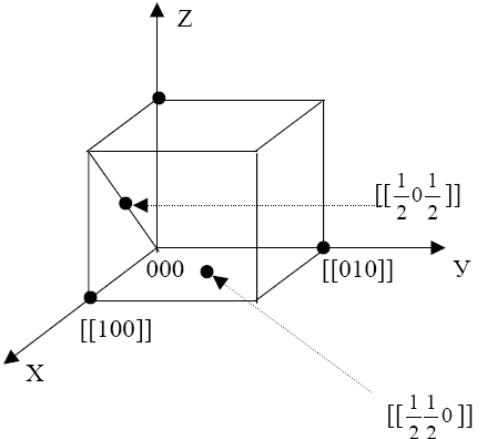
Рис. 1.8.

Символы узловой прямой - [mnp]. Символ <mnp> указывает направление определенного типа. Например, если символ <100> , то он указывает на прямые [100], [010], [001], [ 00], [0 0], [00 ]. Для определения кристаллографических направлений (индексов направлений) по осям в элементарной ячейке необходимо найти проекции вектора на три оси в единицах элементарной ячейки, а затем привести отношение этих координат к отношению трех наименьших целых чисел.

П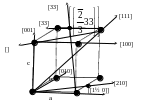 ример:

Рис. 1.9 Обозначения узлов и узловых прямых в простой кубической решетке

Символы узловой плоскости. Индексы Миллера. Пространственную решетку можно представить семейством параллельных узловых плоскостей. Пусть одна из таких плоскостей отсекает на осях координат отрезки A, B, C.

Уравнение такой плоскости в отрезках:

x,y,z – координаты узлов пространственной решетки лежащих в данной плоскости.

Координаты узлов можно записать: x=ma, y=nb, z=pc.

Подставляем значения координат в уравнение получаем:

Так как m, n, p – целые, то - рациональные числа. Отношение между ними равно отношению простых целых чисел h k l.

h k l- индексы Миллера, определяют положение плоскости в кристаллическом пространстве.

Символ плоскости (h k l).

Учитывая пропорциональность индексов

_(*)

_{подставляем их в исходное уравнение плоскости и получаем}

Индексы Миллера определяются следующим образом:

1. Находят отрезки A, B, C, отсекаемые плоскостью на осях координат

2. Находят обратные величины.

3. Если обратные величины дробные, то приводят к общему знаменателю q.

4. Находят h k l из (*).

Пример:

1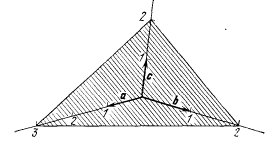 .A=3a B=2b C=2c

2.

3. q=6

4. h= 2 k= 3 l= 3

Индексы Миллера (233).

Индексы Миллера некоторых кристаллографических плоскостей кубической решетки представлены на рисунке 1.10.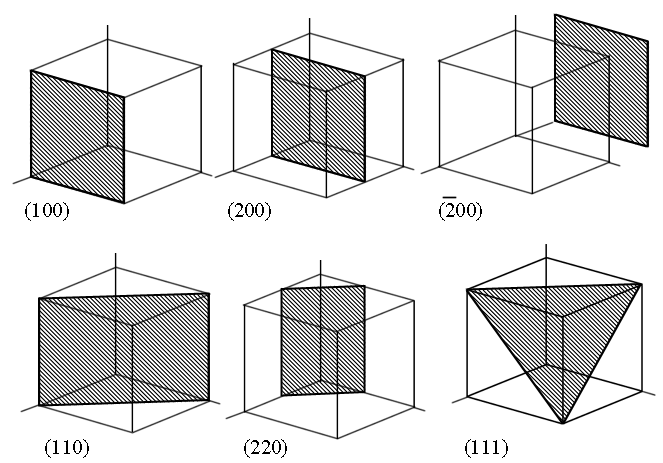

Рис.1.10. Индексы Миллера некоторых кристаллографических плоскостей кубической решетки.

Следует отметить, что прежде чем характеризовать положение узлов, индексы направлений и плоскостей в решётке, необходимо сначала выбрать элементарную ячейку и описать её базис. От координат атомов базиса и выбора периодов элементарной ячейки зависят индексы узлов, направлений и плоскостей в решётке.

1.5.Обратная решетка кристалла. Вектор обратной решетки и его свойства.

Обратная решетка является важным математическим образом, находящим многочисленные применения в геометрической кристаллографии, в теории дифракции и структурном анализе кристаллов, в физике твердого тела. Обратная решетка является математической абстракцией, как и прямая решетка.

Решетка, определяемая тремя векторами называется прямая решетка.

Введем векторы обратной решетки , определяемые уравнениями:

_, (1.4)

(1.5)

Из первой системы уравнений (1.4):  - длина обратного вектора.

Если параллелен , то .

Из 2-ой системы уравнений (1.5)

Так как , то

Аналогично доказывается, что , , , . Следовательно, перпендикулярен плоскости, в которой лежат векторы и .

Вектор перпендикулярен плоскости, в которой лежат векторы и _{, и вектор} перпендикулярен плоскости, содержащей векторы и . Поэтому векторы _{и можно представить выражениями:}

_{, , (1.6)}

_{где 1, 2, 3} – коэффициенты пропорциональности.

В уравнение (1.4) подставим значении из уравнения (1.6). Получим:

_{Так как , где -объем элементарной ячейки, то}

_{. Аналогично и}

Связь векторов обратной решетки и векторов прямой решетки:

_{, , .}

_{, , .}

где ^* - объем элементарной ячейки обратной решетки

Решетка, обратная обратной решетке, будет прямой решеткой.

Связь объемов элементарной ячеек обратной и прямой решеток:

Т ак как ,

то .

Пример: Обратная решетка простой кубической решетки.

Векторы трансляции простой кубической решетки:

Объем элементарной ячейки

Вектор обратной решетки .

Следовательно, обратная решетка является простой кубической решеткой.

Вектор обратной решетки и его свойства

Введем в пространстве обратной решетки вектор , идущий из начального узла в узел с индексами [[hkl]].

Тогда: ,

где h, k, l  целые числа, не имеющие общего множителя.

Свойства вектора обратной решетки:

1. Вектор обратной решетки перпендикулярен плоскости с индексами (hkl).

Доказательство: Докажем, что вектор перпендикулярен двум любым прямым лежащим в плоскости с индексами (hkl). Проведем плоскость (hkl), которая отсекает на осях координат отрезки A, B, C (рис.1.11). Отрезки связаны с индексами:

Рис.1.11.

Проведем на плоскости векторы и :

Составим скалярное произведение:

_{то есть}

Аналогично

_{то есть}

Следовательно, перпендикулярен плоскости (hkl).

2. Длина вектора обратно пропорциональна расстоянию d между плоскостями (hkl) прямой решетки.

Доказательство: Разобъем решетку на семейство параллельных плоскостей с индексами (hkl). Расстояние ближайшей к началу координат плоскости (q=1) равно межплоскостному расстоянию d между любой парой соседних плоскостей. Уравнение плоскости номера q можно записать в виде:

, где - текущий радиус-вектор, - единичный вектор нормали к плоскости; qd – расстояние q-й плоскости от начала координат.

Так как , поэтому

Предполагается, что h, k, l не имеют общего множителя, поэтому вместо Н записан Н’, чтобы отличать от общего случая, когда коэффициенты, определяющие этот вектор, имеют общий множитель.

Таким образом, вектор обратной решетки (характеризующий её узел) с точностью до целого множителя имеет те же индексы, что и плоскости прямой решетки, нормальные к нему. Следовательно, обратная решетка есть совокупность точек (узлов), каждая из которых отображает семейство параллельных атомных плоскостей и имеет те же индексы (с точностью до общего множителя).

Физический смысл обратной решетки

Поскольку ориентация плоскости в пространстве может быть задана не только расположением лежащих в ней точек, но также и направлением нормали к этой плоскости, то введение понятия “обратной решетки” приводит по существу к тому, что задание ориентации плоскости в пространстве осуществляется с помощью её нормали, т.е. вектора обратной решетки.

Нормаль обладает числом измерений на единицу меньшим, чем плоскость, что создает преимущество простоты, особенно в тех случаях, когда одновременно рассматривается совокупность большого числа плоскостей. Одновременно, в ряде случаев, при введении понятия обратной решетки упрощается и математическая интерпретация.