1.Структура кристаллов.
1.1.Кристаллическая решетка. Элементарная ячейка. Базис.
Кристаллы состоят из атомов, периодически расположенных в пространстве по параллельным плоскостям и прямым. Конкретное расположение атомов в кристалле называется структурой вещества или кристаллической решеткой. Характер расположения атомов в веществе можно описать пространственной решеткой. Пространственная решетка является математической абстракцией, описывающей периодичность кристаллической структуры. Атомы в кристалле имеют заметные геометрические размеры и находятся в тепловых колебаниях относительно некоторых центров равновесия. Такие центры равновесия, отвечающие атомам одинакового сорта, называются узлами (узлы – точки с равной электронной плотностью). Группа атомов, связанная с узлом кристаллической решетки, называется базисом. Пояснение разницы между узловым рядом (пространственная решетка) и одномерной структурой (кристаллическая решетка) показано на рисунке 1.1.
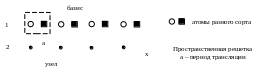
Рис.1.1. Одномерная атомная структура (1) и отвечающая ей узловая прямая (2)
|
Рис.1.2. Пространственные решетки трех одномерных кристаллических решеток |
Процесс воссоздания кристалла по его пространственной решетке можно описать условной формулой:
кристалл = пространственная решетка + базис.
Определим идеальный
кристалл как тело, состоящее из атомов,
расположенных в пространственной
решетке так, что можно ввести три вектора
основных
трансляций
![]() ,
обладающих следующим свойством. При
рассмотрении этой атомной решетки из
произвольной точки
,
обладающих следующим свойством. При
рассмотрении этой атомной решетки из
произвольной точки
![]() решетка имеет тот же вид что и при
рассмотрении из точки
решетка имеет тот же вид что и при
рассмотрении из точки
![]() :
:
![]() , (1.1)
, (1.1)
где m,
n,
p
– произвольные целые числа. Иногда
векторы основных трансляций обозначаются![]() .
.
Совокупность точек, определяемая соотношением (1.1) при различных значениях чисел m, n, p , определяет кристаллическую решетку.
Операция перемещения кристалла как целого параллельного самому себе, описываемую вектором
![]() , (1.2)
, (1.2)
называется трансляцией.
Вектор трансляции
![]() кристаллической решетки связывает
любые две точки решетки.
кристаллической решетки связывает
любые две точки решетки.
Описание
структуры любого кристалла принято
проводить, охарактеризовав его
элементарную ячейку. Кристаллическая
структура строится бесконечным
параллельным повторением параллелепипеда,
построенного на векторах основных
трансляций
![]() .
Такой
параллелепипед называется элементарной
ячейкой.
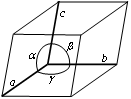
Элементарная
ячейка в общем случае имеет форму
косоугольного параллелепипеда (смотри
рис.1.3).
.
Такой
параллелепипед называется элементарной
ячейкой.
Элементарная
ячейка в общем случае имеет форму
косоугольного параллелепипеда (смотри
рис.1.3).
|
Рис.1.3. Элементарная ячейка. |
Объем элементарной ячейки, построенной на векторах трансляции выражается тройным смешанным произведением
![]() (1.3)
(1.3)
Раскрыв это выражение находим:
![]()
Пример:
Для гексагональной
системы (a=b
и ==90,
=120)
= a2c![]()
Для ромбической системы (===90) = abc.
Выбрать элементарную ячейку одного и того же кристалла можно несколькими способами. При таком выборе стремятся к наиболее простой форме ячейки, в частности к наибольшему числу прямых углов, а также к минимальности ее объема. Ячейку с наименьшим объемом принято называть примитивной элементарной ячейкой.
Примитивная ячейка – это элементарная ячейка с минимальным объемом, на примитивную ячейку приходится один узел. Число атомов в примитивной ячейке равно числу атомов базиса. Вектора в этом случае называются вектора примитивных трансляций. Выбор примитивных векторов трансляции неоднозначен, как и выбор элементарной ячейки (рис.1.4).
|
Рис.1.4. Неоднозначный выбор примитивных векторов трансляции для двухмерной кристаллической решетки |
Примитивная ячейка есть важнейший элемент теории кристаллов, однако, чаще всего ее симметрия ниже симметрии пространственной решетки кристалла и, тем более, самого кристалла. Симметрию, совпадающую с полной симметрией решетки, имеет примитивная ячейка Вигнера-Зейтца, определяемая как область пространства, все точки которой расположены к данному узлу решетки ближе, чем к любому другому узлу.
Построение ячейки Вигнера-Зейтца:
|
Рис. 1.5. Построение элементарной ячейки Вигнера-Зейтца для двумерной косоугольной решетки |
2) строим плоскости, перпендикулярные к этим отрезкам и
проходящие через их середины;
3) выбираем наименьший многогранник, ограниченный по-
строенными плоскостями и содержащий выбранный узел
решетки.
Примитивная ячейка Вигнера-Зейтца – имеет наименьший объем, можно заполнить все пространство кристаллической решетки.
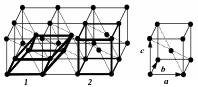
Часто выбирают элементарную ячейку большего объема, но более простой формы, содержащую несколько наборов атомов, формирующих базис элементарной ячейки. Такую ячейку будем называть условной (сложной) элементарной ячейкой. На рис. 1.6 изображена так называемая объемно-центрированной кубическая кристаллическая (ОЦК) решетка. Элементарную ячейку в этой решетке можно выбрать как косоугольный параллелепипед (1) с квадратным основанием (примитивная ячейка). Однако за элементарную удобнее выбрать ячейку в 2 раза большего объема, но со всеми прямыми углами (2) (условная ячейка). Такая условная элементарная ячейка гораздо нагляднее отражает симметричность в расположении атомов, ее легче анализировать математически.
|
Рис.1.6. Выбор элементарной ячейки ОЦК решетки |
Число узлов, приходящихся на условную ячейку, равно числу атомов базиса.
В таком случае удобно подробно охарактеризовать расположение атомов базиса в пределах одной элементарной ячейки, а всю структуру кристалла получить трансляцией данной ячейки, осуществляя параллельные переносы на векторы трансляции .
Базис
принято задавать, описав положения всех
атомов в одной ячейке набором
радиус-векторов
![]() ,
числа
,
числа
![]() задают
положения атомов в долях соответственно
векторов
задают
положения атомов в долях соответственно
векторов![]() .
.