10. Расчет переходных процессов в скорректированной системе.
Рассчитаем переходные процессы в скорректированной системе, обусловленные ступенчатым приложением задающего воздействия uз = 5 В и ступенчатым изменением момента сопротивления на величину Мс = 70 Н·м.
Для расчета переходных процессов воспользуемся изображением регулируемой величины (4.8)
,
где Wyx(p) – передаточная функция замкнутой системы для регулируемой величины Ω по
задающему напряжению UЗ;
Wyf(p) – передаточная функция замкнутой системы для регулируемой величины Ω по моменту сопротивления MC .
Подставим выражения передаточных функций Wyx(p), Wyf(p) и получим операторные уравнение для регулируемой величины:
а) до введения корректирующего звена
, (10.1)
б) после введения корректирующего звена
. (10.2)
Скачкообразно приложенные ступенчатые воздействия в изображениях по Лапласу
(10.3)
.
Используя обратное преобразование Лапласа в программе MathCAD, находим оригинал регулируемой величины
а) до введения корректирующего звена
, (10.4)
б) после введения корректирующего звена
. (10.5)
В программе MathCAD построим графики переходных процессов при ступенчатом приложением задающего воздействия uз = 5 В.
Н
. (10.6)
рад/с .
Рисунок 10.1 – Переходный процесс в системе до введения корректирующего устройства
при изменении задающего напряжения uз = 5 В.
Рисунок 10.2 – Переходный процесс в системе после введении корректирующего
устройства при изменении задающего напряжения uз = 5 В.
В программе MathCAD построим графики переходных процессов при ступенчатом изменение момента сопротивления на величину Мс = 70 Н·м.
Н
. (10.7)
рад/с .
Рисунок 10.3 – Переходный процесс в системе до введения корректирующего устройства
при ступенчатом изменение момента сопротивления на величину Мс = 70 Н·м.
Рисунок 10.4 – Переходный процесс в системе после введения корректирующего
устройства при ступенчатом изменение момента сопротивления
на величину Мс = 70 Н·м.
В программе Matlab смоделируем переходные процессы в скорректированной системе обусловленные ступенчатым приложением задающего воздействия uз = 5 В и ступенчатым изменением момента сопротивления на величину Мс = 70 Н·м.
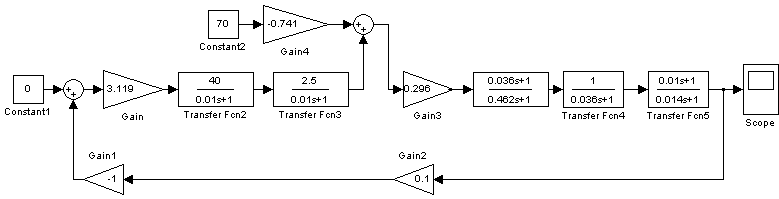
Рисунок 10.5 – Структурная схема скорректированной САР.
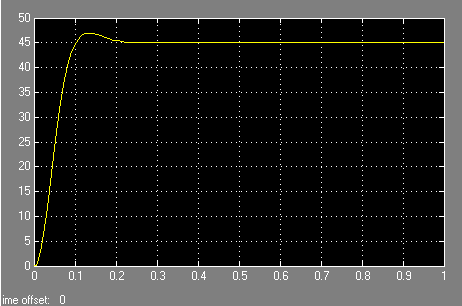
Рисунок 10.6 – Переходный процесс в системе после введении корректирующего
устройства при изменении задающего напряжения uз = 5 В.
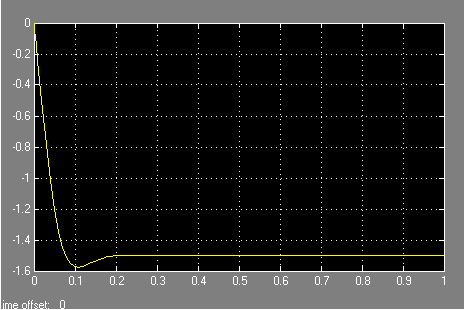
Рисунок 10.7 – Переходный процесс в системе после введения корректирующего
устройства при ступенчатом изменение момента сопротивления
на величину Мс = 70 Н·м.
Из полученных графиков переходных процессов видно что время регулирования в скорректированной системе tP ≈ 0,1 с, а перерегулирование σ не более 5%, следовательно переходный процесс в скорректированной системе полностью удовлетворяет заданным требованиям качества.