Общая постановка задачи оптимального управления.

В фазовом пространстве даны x⁰ и x¹. Среди всех допустимых управлений u=u(t), переводящих фазовую точку из x⁰ в x¹, найти такое (если оно существует), для которого функционал:

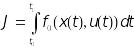(8)

принимает наименьшее возможное значение. Здесь x(t) – решение системы (5) ДУ с начальным условием x(t₀) = x⁰, с соответствующим управлением u(t); t₁ – момент прохождения траектории через точку x¹; функция f₀ – подынтегральная функция, определена и непрерывна вместе с частными производными на всем пространстве

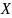* , где – область допустимых управлений, а – фазовое пространство.

Заметим, что все f_i, i=1,2,…,n и все непрерывны, а система (5) ДУ автономна, т.е. правая часть явно не зависит от времени.

Система (5) неавтономна, а функционал имеет вид:

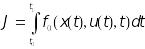. (9)

Определение: задан функционал (9), если в каждой функции x(t) (кривой) из некоторого класса функций поставлено в соответствие некоторое число

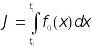(10)

или функционал имеет вид:

где t₀≤t≤t₁, то 1) t₀ и t₁ могут быть заданы. И время перехода есть t₁-t₀.

2) t₁ может быть не задано, а определено из условия прохождения фазовой точки x(t) по траектории через заданную точку x¹, т.е. x(t)=x₁, откуда и “вытекает” t₁ и x(t) – решение системы (5).

При этом t₁ находится из:

x₁(t)=x¹₁

x₂(t)=x¹₂

……………..

x_n(t)=x¹_n . (11)

Важным частным случаем общей задачи оптимального управления является случай, когда f₀(x,u)≡1 в (8).

Тогда (8) имеет вид:

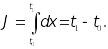(12)

Билет №4 (Сопряженная система. Гамильтониан)

Принцип оптимальности Понтрягина.

Для формулировки необходимого условия оптимальности удобно дать иную формулировку задачи оптимального управления.

Добавим к фазовым координатам x₁, x₂, …, x_n, меняющимся по закону (11) еще одну координату x₀, закон изменения которой имеет вид:

, (13)

где f₀ – подынтегральная функция из (8). Тогда будем рассматривать новую систему ДУ:

(14)

Или в векторном виде:

(15)

где = {x₀, x}, размерностью n+1, а = {f₀,f} – вектор правых частей ДУ.

Геометрическая интерпретация (рис.6).

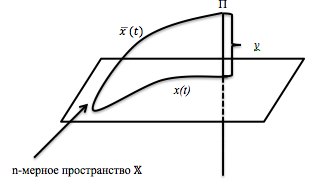
Рис.6

Переходим к формулировке теоремы Понтрягина, дающей решение основной общей задаче оптимального управления.

Рассмотрим еще одну систему относительно вспомогательных (сопряженных) ψ₀,ψ₁,…,ψ_n:

(16)

где f₂ взято из (14).

Это система n+1 линейных ДУ относительно n+1 переменных с постоянными коэффициентами. Вводим вектор сопряженных переменных ψ={ψ₀,ψ₁,…,ψ_n}. Тогда имеем:

(17)

где – матрица производных функции .

Если выбрано некоторое допустимое управление u(t), t₀≤t≤t_1, то имеем соответствующую фазовую траекторию 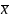(t) системы (14) с начальным условием (t₀)={0,x₀}, а система (16) имеет вид:

(18)

и эта система ДУ является однородной, поэтому при любых начальных значениях (условиях) ψ_i допускает единственное решение.

Как и решение (t), решение системы (18) состоит из непрерывных функций ψ_i(t)_,

имеющих всюду непрерывные производные по t.

Объединим системы (18) и (14). Для этого введем гамильтонову функцию (гамильтониан) H(x₁,x₂,…,x_n,u₁,u₂,…u_r):

(19)

либо в виде гамильтоновой системы:

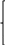
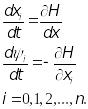(20)

Взяв произвольно допустимые (т.е. кусочно-непрерывные) управления u(t), t₀≤t≤t₁ и начальные условия (t₀)= ⁰, мы можем найти соответствующую траекторию

(t) = {x₀(t),x₁(t),…x_n(t)}. После этого мы можем находить вектор-функцию (t) = {ψ₀(t),ψ₁(t),…ψ_n(t)}, соответствующую (t) и u(t).

При фиксированных постоянных значениях и , функция гамильтониана H становится функцией параметра u (u ).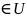

Точную верхнюю грань этой функции мы обозначим через M( , x):

M( , x) = sup H( , x, u). (21)

Точная верхняя грань функции – наименьшее решение из верхних граней, для которого значение функции на заданном интервале будет меньше (11). Если точная верхняя грань значений непрерывной функции H достигается в некоторой области , то M( , x) – есть максимум функции H при фиксированных переменных и .