Билет №1 (Управляемые объекты. Фазовые траектории. Процесс управления)

Понятие об управляемых объектах.

Рассмотрим, например, прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля характеризуется двумя числами: путь S, скорость V. Две эти величины меняются в зависимости от времени t, но не самопроизвольно, а сообразно воле водителя, управляющего работой двигателя, увеличивая или уменьшая развиваемую двигателем силу F.

Схема управляемого объекта (рис. 1):

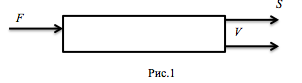
Величины S и V, характеризующие состояние объекта – фазовые координаты, величина F – управляющий параметр.

Если рассматривать движение автомобиля не на прямой, а на плоскости, то фазовых координат будет 4 (2 географические компоненты и 2 компоненты скорости), а управляющих параметров будет 2: мощность двигателя (сила тяги) и угол поворота руля.

У летящего самолета можно рассматривать 6 фазовых координат: 3 географические компоненты и 3 компоненты скорости V_x, V_y, V_z; несколько управляющих параметров: F и φ – величины, характеризующие положение рулей высоты и направления и тягу двигателя.

В электрическом утюге с терморегулятором фазовыми координатами будут сила тока и температура нагрева, а управляющим параметром – положение регулятора.

Таким образом, мы имеем следующее математическое описание управляющего объекта: состояние объекта задается в каждый момент времени числами x₁, x₂, …, x_n, которые называются фазовыми координатами. Движение объекта, с математической точки зрения, заключается в том, что его состояние изменяется с течением времени (x₁, x₂, …, x_n – переменные величины). Движение объекта происходит не самопроизвольно: объектом можно управлять “рулями”, положение которых характеризуется в каждый момент времени r числами: u₁, u₂, …, u_r. Эти числа – управляющие параметры. “Рулями” можно манипулировать – по своему желанию изменять u₁, u₂, …, u_r с течением времени (функция времени).

Предположим, что, зная фазовое состояние объекта в t₀ и выбрав управляющие функции u₁(t), u₂(t), …, u_r(t), мы сможем математически точно рассчитать поведение объекта для любых t>t₀ и найти x₁(t), x₂(t), …, x_n(t), характеризующие изменение фазовых координат с течением времени.

Схема объекта в теории автоматического управления (ТАУ) (рис.2):

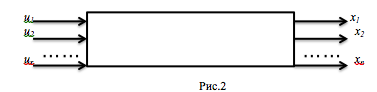
u₁, u₂, …, u_r – входные переменные, x₁, x₂, …, x_n – выходные переменные в ТАУ.

Величины {u_r} удобно считать координатами некоторого вектора u, который будет называться управляющим вектором. Введем n-мерный вектор x = { x₁, x₂, …, x_n }, заданный в n-мерном пространстве. Это n-мерное пространство, в котором в виде точек изображаются фазовые состояния объекта, называется фазовым пространством.

Чтобы полностью задать движение объекта надо задать его начальное фазовое состояние в t₀ и выбрать управляющие функции u₁(t), u₂(t), …, u_r(t), t≥t₀, т.е. выбрать вектор-функцию u(t) = { u₁(t), u₂(t), …, u_r(t) }. Задав все эти параметры, мы однозначно определяем дальнейшее движение. Оно заключается в том, что фазовая точка x(t) для t>t₀ с течением времени перемещается в фазовом пространстве и описывает некоторую линию-траекторию (рис.3).

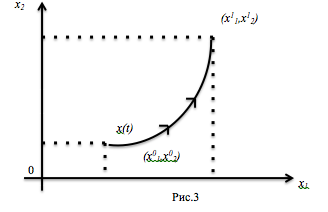
Пара вектор-функций x(t) и u(t) – процесс управления (или просто - процесс).